ノンパラメトリック検定（読み）ノンパラメトリックけんてい（英語表記）non-parametric test（英），test non parame´trique（仏），Nichtparametrischer Test（独）

最新 心理学事典

ノンパラメトリックけんてい
ノンパラメトリック検定
non-parametric test（英），test non parame´trique（仏），Nichtparametrischer Test（独）

心理学で使われる統計的仮説検定の手法の多くは，母集団の確率分布が正規分布であることを前提としている。これに対して，母集団の確率分布の型を特定しない仮説検定の手法を，母集団の確率分布に含まれる母数によらないという意味で，ノンパラメトリック検定とよぶ。ノンパラメトリック検定は，母集団に正規分布を仮定できない場合，変数が順序尺度で測定されている場合など，適用できる範囲が幅広い。ただし，母集団の確率分布を特定しないが，データが独立に同一の分布から標本抽出されていることを仮定している。

【対応のない標本のノンパラメトリック検定】　二つの母集団からそれぞれ独立に標本が得られるとき，二つの母集団の分布が正規分布に従う場合，二つの母集団の平均が等しいかどうかの検定には，対応のないｔ検定ｔ-testが用いられる。マン-ホイトニーのＵ検定Mann-Whitney U testは，対応のないｔ検定の代わりに用いる，対応のない2標本のノンパラメトリック検定の一つである。二つの群の人数がそれぞれｎ¹人とｎ²人で，一方の標本をｘ¹，ｘ²，…，ｘⁿ¹とし，他方の標本をｙ¹，ｙ²，…，ｙⁿ²とする。ｘⁱとｙ^jの組み合わせはｎ¹ｎ²通りあるが，位置母数（正規分布の母平均に当たる）が等しいという帰無仮説が真ならば，ｘⁱがｙ^jを上回る組み合わせの数は全体の半分つまりｎ¹ｎ²/2付近の値となる。このことを利用し，マン-ホイトニーのＵ検定は，ｎ¹個のｘⁱがｎ²個のｙ^jを上回る総数（これをＵとする）を検定統計量とする。標本サイズが小さいときにはＵの棄却域の数表が与えられている。標本サイズが大きいときには，帰無仮説のもとでＵは平均がｎ¹ｎ²/2，分散が（ｎ¹＋ｎ²＋1）/12の正規分布に近似的に従うことを利用して検定を行なう。

　ウィルコクソンの順位和検定Wilcoxon rank sum testも，対応のない2標本のノンパラメトリック検定の一つである。ｘ¹，ｘ²，…，ｘⁿ¹とｙ¹，ｙ²，…，ｙⁿ²をこみにして小さい方から順位をつけたとき，帰無仮説が真ならば，一方の群の順位の平均が（ｎ¹＋ｎ²＋1）/2付近の値となることを利用する。実際には平均順位ではなく，人数で割らない順位和の棄却域が数表にされている。ｘ¹，ｘ²，…，ｘⁿ¹の順位和をＲ¹とすると，Ｕ＝Ｒ¹－ｎ¹（ｎ¹＋1）/2という関係がある。つまりウィルコクソンの順位和検定はマン-ホイトニーのＵ検定と同等なので，両者をまとめてマン-ホイトニー-ウィルコクソン検定（あるいはウィルコクソン-マン-ホイトニー検定）とよぶことがある。

　マン-ホイトニー-ウィルコクソン検定は検定力が高く，母集団の確率分布が正規分布でなければ，しばしば検定力がｔ検定を上回る。しかし，尺度母数（正規分布の母分散に当たる）が等しくない場合，第一種の誤りが統制されない。

　3標本以上の場合には，分散分析の代わりにクラスカル-ウォリスの検定Kruskal-Wallis testを用いる。この検定は，群の数が二つの場合には，マン-ホイトニー-ウィルコクソン検定と同等である。テューキーTukeyのHSD法の代わりの多重比較には，スティール-ドゥワスSteel-Dwassの方法を用いる。

　中央値検定median testは，母集団の中央値が等しいという帰無仮説を検定する方法である。中央値検定では，すべて群のデータをこみにしたときの中央値を求め，各群のデータをこの中央値より大きいものと中央値以下のものに二分し，クロス表にする。帰無仮説が真ならば，どの群でもデータがこの中央値を境にほぼ半々になるため，このことを利用してクロス表の独立性検定を行なう。中央値検定には，3標本以上でも実行できる，尺度母数が等しいことを前提としない，クロス表の独立性検定であるため特別な数表を必要としないという利点がある。しかし，検定力はマン-ホイトニー-ウィルコクソン検定に劣る場合がある。

【対応のある標本のノンパラメトリック検定】　対応のある2標本があるとき，母平均が等しいという仮説の検定には，対応のあるｔ検定を用いる。符号検定sign testは，対応のあるｔ検定の代わりに用いる，対応のある2標本のノンパラメトリック検定の一つである。人数がｎ人で，観測値の対を（ｘ¹，ｙ¹），（ｘ²，ｙ²），…，（ｘⁿ，ｙⁿ）とする。ｄⁱ＝ｘⁱ－ｙⁱとするとき，対応のあるｔ検定では，ｄ¹，ｄ²，…，ｄⁿの母平均が0であるという帰無仮説を立て，ｔ統計量を計算する。符号検定では，ｄ¹，ｄ²，…，ｄⁿの符号のみに注目し，符号が正となる母比率が0.5であるという帰無仮説を立て，二項検定を行なう。

　ウィルコクソンの符号付き順位検定Wilcoxon signed rank testも対応のある2標本のノンパラメトリック検定の一つである。差得点ｄ¹，ｄ²，…，ｄⁿの絶対値｜ｄ¹｜，｜ｄ²｜，…，｜ｄⁿ｜に順位をつけ，ｄⁱの符号が正であるものの順位を合計する。標本サイズが小さいときには数表が与えられているが，標本サイズが大きいときには，帰無仮説のもとで，この順位和は平均がｎ（ｎ＋1）/4，分散がｎ（ｎ＋1）（2ｎ＋1）/24の正規分布に近似的に従うことを利用して検定を行なう。ウィルコクソンの符号付き順位検定は差得点の絶対値を使用するため，差得点の大きさに意味のない順序尺度の変数には適用できない。

　群の数が三つ以上の場合にはフリードマンの検定Friedman testを用いる。フリードマンの検定は，群の数が二つの場合には，符号検定と同等である。

【二変数の関係のノンパラメトリック検定】　間隔尺度または比尺度で測定される二変数の関係の強さは，ピアソンの積率相関係数で表わすことが多い。ケンドールの順位相関係数Kendall's rank correlation coefficientは二変数の関係の強さを表わすノンパラメトリックな指標の一つである。人数がｎ人で，観測値の対を（ｘ¹，ｙ¹），（ｘ²，ｙ²），…，（ｘⁿ，ｙⁿ）とする。参加者を2人ずつ取り出したときに，大小関係が同じ方向，つまりｘⁱ＞ｘ^jかつｙⁱ＞ｙ^jあるいはｘⁱ＜ｘ^jかつｙⁱ＜ｙ^jとなる参加者の組み合わせの数をＰとし，大小関係が逆方向，つまりｘⁱ＞ｘ^jかつｙⁱ＜ｙ^jあるいはｘⁱ＜ｘ^jかつｙⁱ＞ｙ^jとなる組み合わせの数をＱとする。参加者の組み合わせの総数をＴ（＝ｎ（ｎ－1）/2）としたとき，（P－Q）/Ｔをケンドールのτ^a（タウ エー）という。また，ｘⁱ＝ｘ^jである組み合わせの数をＴ^x，ｙⁱ＝ｙ^jである組み合わせの数をＴ^yとしたとき，



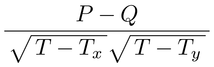
をケンドールのτ^b（タウ ビー）という。ケンドールの順位相関係数は，大小関係がすべて同方向ならば＋1，すべて逆方向ならば－1，同方向と逆方向の数が等しければ0となる。

　標本サイズが大きいとき，ケンドールのτ^aは，二変数が無関係であるという帰無仮説が真ならば，平均が0，分散が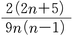である正規分布に近似的に従う。このことを利用して無相関検定が実行できる。

　2変数の関係の強さを表わすノンパラメトリックな指標は，測定値を順位に直したときの相関係数である，スピアマンの順位相関係数Spearman's rank correlation coefficientもある。無相関検定は，ピアソンの積率相関係数の無相関検定の式にスピアマンの順位相関係数を代入して行なう。　→相関係数　→統計的推論
〔橋本 貴充〕

出典　最新 心理学事典