仮説検定（読み）カセツケンテイ

デジタル大辞泉

かせつ‐けんてい【仮説検定】

統計学で、母集団から抽出した標本が、母集団全体を説明する統計的仮説を支持するかを判定すること。実際に観測された標本が、ある仮説に従う母数または確率分布をもつ母集団から抽出される確率を求め、有意水準と比較して仮説の当否を判断する。統計的仮説検定。検定。
[補説]1回の実験で、3回連続して1の目が出たサイコロがあったとし、これについて仮説検定を試みる。まず、このサイコロがいかさまではないという帰無仮説を立てる。正しいサイコロが同様の目を出す確率は二項分布に従うため、1/216と求められる。有意水準を1パーセントとすると、この帰無仮説は棄却され、サイコロはいかさまであるという対立仮説が成立する。

出典　小学館

精選版 日本国語大辞典

かせつ‐けんてい【仮説検定】

1. 〘 名詞 〙 ある主張が正しいかどうかを統計的方法により判定すること。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

仮説検定
かせつけんてい

数理統計学において、母集団に関する仮説を標本値をもとにして検定すること。たとえば、さいころを4回投げて4回とも6の目が出たとする。このさいころは正常といえるか？　正常なさいころであっても4回とも6の目が出ることはありうる。しかしこのようになる確率は(1/6)⁴≒0.00077であって非常に小さく、常識的にはこのさいころは正常でないといいたいところである。

　このような問題に対して、確率的な考えを用い、さらにある実践上の規約を設けて対処するのが仮設検定の方法であって、その基本的な考えを簡単な型について説明する。

［古屋　茂］

仮説検定と帰無仮説

初めに母集団の分布Fについて仮説Hを置く。次に小さな数α（危険率とよばれるもので普通は0.01または0.05にとる）を定めておく。次に分布Fをもつ確率変数Xに対して、実数の領域Rを、Xの値がRに属する確率がたかだかαに等しいようにあらかじめ定めておく。

　こうしておいて、試行の結果得られたXの値xがRに属したとすると、もし仮説Hが正しければ、まれにしかおこらないこと（確率がαより小さい）がおこったことになるので、仮説Hは疑わしいとしてHを捨てることにする。これは確率的背理法とでもいえる論法である。また、もし試行の結果得られたXの値xがRに属さない場合にはHは捨てないことにする。捨てないといっても、これだけの理由では捨てることができないというだけで、積極的にHが正しいと主張するのではない。

　以上が仮説検定の考えである。この考えを初めにあげたさいころの場合に適用すると、Hは「さいころは正常である。すなわちどの目の出る確率も1/6である」であり、確率変数Xの分布は二項分布B(4,1/6)である。またRとしてR₁＝｛x|x≧4｝をとると
　　P(X∈R₁)＝P(X＝4)＝(1/6)⁴＜0.01
となり、危険率0.01に関してHは捨てられる。すなわち、このさいころは正常とはいえない（危険率0.01で）ということになる。

　一般に、仮説を置くとき、初めから捨てられることが予想されている場合が多い。R・A・フィッシャーはこれを帰無仮説と名づけた。

［古屋　茂］

適合度の検定">χ²（カイ二乗）検定法と適合度の検定

次の式（＊）の形のχ²を用いる検定法をχ²検定法という。χ²検定法は比率の検定、独立性の検定にも利用されるが、ここでは適合度の検定にχ²検定法を用いる。

　全体でk通りの場合があり、n回の実験または観測において結果が各場合に属する回数がf₁，f₂,……，f_kであったとする。一方、想定された分布において各場合のおこる確率がp₁,p₂,……，p_kであるとする。このとき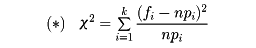

は、想定された分布と実験による分布との適合の度合いをみるときに用いられる。すなわち適合していればχ₂の値は小さく、適合していなければχ₂の値は大きい。なおここで各場合についてnp_i≧10となるようにしておく。そうでないときは、いくつかの場合をまとめることによってnp_i≧10が成り立つようにしておく。

　前記のf₁，f₂,……，f_kはそれぞれ確率変数Z₁，Z₂,……，Z_kの実現値と考えられる。Z₁，Z₂,……，Z_kの確率分布は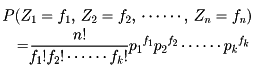

で与えられる。したがって（＊）のχ₂は確率変数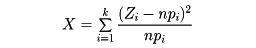

の実現値である。

　この確率変数Xの確率分布は、np_i≧10が成り立つとき、自由度k－1のχ₂分布に近い。

　このことを利用して、「想定された分布が適合している」という仮説Hを検定することができる。すなわち、危険率を0.01にとるとすると、自由度k－1のχ₂分布の表をみて
　　P(X＞λ)＝0.01
のようにλを定める。（＊）のχ₂がχ₂＞λであれば仮説Hは捨てられ、χ₂≦λであればHは捨てることができない。この検定を適合度の検定という。

［古屋　茂］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

仮説検定
かせつけんてい
testing of statistical hypothesis

数理統計学において，未知母数について立てられた仮説命題を，標本 (データ) をもとに検証する統計的判断の方式をいう。基本的には R.A.フィッシャーの導入した有意性検定に準拠している。すなわち，まず未知母数を θ とし，θ の値が θ₀ であるとする命題を仮説 (帰無仮説という) として設定する。これを H：θ＝θ₀ と書く。次に大きさ n の標本 X₁ ，X₂ ，…，X_n を選んでその実現値 ( x₁ ，x₂ ，…，x_n ) について，仮説 H が正しければあるごく小さい確率αでしか現れない実現値の範囲，すなわち棄却域 W を設定しておき，実現値が棄却域に入れば H を棄却し，棄却域以外にあれば H を受容する。確率αを検定の危険率あるいは有意水準という。 H を棄却するにしても受容するにしても，当然その判断は絶対的なものではなく，H が真であるのにこれを棄却するという第1種の過誤と，H が真でないのに受容するという第2種の過誤を犯すことがありうる。第1種の過誤を犯す確率が危険率αであり，第2種の過誤は θ≠θ₀ とする対立仮説 H'：θ≠θ₀ に対する危険率 α' であるが，後者は W や H' の定め方に依存し，これを最小にする検定が望ましい検定とされ，ここに検定の優劣比較の理論 (→検定論 ) が成立する。対立仮説を持出す考え方は主として J.ネイマンと E.ピアソンによって提唱されたが，フィッシャーはみずからの信念を歪曲するものとして激しい論争が生じた。ネイマンとピアソンが証明した基本定理，すなわち「尤度比を検定統計量にとれば第2種の過誤の確率が最小になる」ということは，数理統計学における最も強く，最も役に立つ理論的結果である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

仮説検定【かせつけんてい】

単に検定とも。母集団について立てた仮説（帰無仮説）H(/0)を捨てるか捨てないかを，母集団から抽出した標本（測定値）によって定めること。H(/0)が成立すると仮定して母集団から任意にn個の標本の組を抽出したときの分布を調べ，それが（100−α）％の確率で存在する範囲を決め，実際に測定したn個の値の組がその範囲の外（棄却域）に落ちればH(/0)を捨て，その範囲内にあればH(/0)を捨てない。αを危険率または有意水準といい，普通５％または１％にとる。この場合，仮説H(/0)が正しいのに測定値によってH(/0)を捨てる誤りを第１種の誤りといい，その確率が危険率である。H(/0)が正しくないのにH(/0)を捨てない誤りを第２種の誤りという。
→関連項目F分布｜χ²分布｜推測統計学｜t分布

出典　株式会社平凡社