ワイアシュトラース（読み）わいあしゅとらーす（その他表記）Karl Weierstrass

デジタル大辞泉

ワイアシュトラース（Karl Theodor Weierstrass）

［1815～1897］ドイツの数学者。冪べき級数を用いて複素数が変数の場合の関数論を基礎づけ、また微分できない連続関数を発見。ワイエルシュトラス。

出典　小学館

日本大百科全書(ニッポニカ)

ワイアシュトラース
わいあしゅとらーす
Karl Weierstrass
（1815―1897）

ドイツの数学者。ミュンスターに近い小さな町オステンフェルデに生まれる。父は期待を寄せ、ボン大学へ進ませた。そして政治学を学ばせようとしたが、彼は、プリュッカーの新しい方法による幾何学の講義以外は何も聴かず、卒業の見込みもないまま郷里へ帰った。ついでミュンスター大学でギムナジウムの教員資格検定試験の準備を始めたが、ここでもグデルマンChristoph Gudermann（1798―1852）の数学の講義に出ただけで、他の講義には出ていない。グデルマンのべき級数（整級数）を用いる方法はワイアシュトラースに大きな影響を与えた。1841年、検定試験に合格したが、数学教員の職はなく、僻地(へきち)のギムナジウムで体操の教員となった。15年間、体操を教えながら、アーベル関数を研究した。その研究成果の一部が「アーベル関数論について」と題してクレレが発行している数学雑誌の1854年号に出たのをケーニヒスベルク大学（現、イマヌエル・カント・バルト連邦大学）のリシェロトFriedrich Julius Richelot（1808―1875）が賞賛し、1856年この大学から名誉博士を受けた。同年秋、ベルリン大学助教授になり、1864年には教授に昇格、また各国の科学アカデミー会員に迎えられた。

　ライフワークはアーベル関数の研究であった。「一般の関数」について直観に頼ることを極力避けて追究し、複素数が変数の場合には、グデルマンの方法に倣い、べき級数を出発点とし、「関数要素」とそれの「解析的接続」を導入して、「解析関数」を定義してワイアシュトラース流「関数論」を樹立した。そして、これを土台としてアーベル関数の統一的研究に入った。

　もっとも簡単な楕円(だえん)関数として「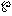(ぺー)関数」を解析的に構成し、「任意の楕円関数は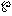関数で表現することができる」ことを証明し、楕円関数を研究するには、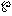関数を研究すれば十分であることへ導いた。超楕円積分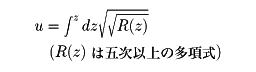

の逆関数（アーベル関数）において、五次と六次の場合は解決されているので、R（z）が任意の次数の場合に取り組み、これを解決したのである。

［小堀　憲　2018年12月13日］

[参照項目] | 整級数 | 楕円積分 | プリュッカー | ワイアシュトラースの多項式近似定理

出典　小学館　日本大百科全書(ニッポニカ)