三段論法（読み）サンダンロンポウ（その他表記）syllogism

デジタル大辞泉

さんだん‐ろんぽう〔‐ロンパフ〕【三段論法】

論理学で、大前提・小前提および結論からなる間接推理による推論式。例えば、「人間は死ぬ」（大前提）、「ソクラテスは人間である」（小前提）、故に「ソクラテスは死ぬ」（結論）の類。

出典　小学館

精選版 日本国語大辞典

さんだん‐ろんぽう‥ロンパフ【三段論法】

1. 〘 名詞 〙 二つの前提命題から一つの結論命題を導く論理的推理をいう。たとえば、「すべての人間は動物である」「Ａ氏は人間である」「故にＡ氏は動物である」とする推論の類。三段推理法。三段法。〔附音挿図英和字彙（1873）〕
   1. [初出の実例]「一層奇抜な其質問は立派に三段論法の形式を具へてゐた」(出典：明暗（1916）〈夏目漱石〉七四)

三段論法の語誌

幕末明治初期に英語 syllogism の訳語として考案された新漢語。「改正増補英和対訳袖珍辞書」（一八六六）では、「三段ノ話法」と訳されていたが、「附音挿図英和字彙」で「三段論法」の形に整えられた。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

三段論法 (さんだんろんぽう)
syllogism

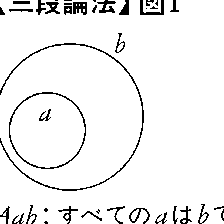
アリストテレスによってほぼその全体が与えられ，中世を通じて洗練された論理学の体系は，現代論理学に対して伝統的論理学と呼ばれているが，三段論法はその主要部門であり〈二つの前提命題から一つの結論命題を得る推論〉と要約される。伝統的論理学においては，おもに〈すべてのaはbである（Aabと略記）〉〈或るaはbである（Iabと略記）〉〈いかなるaもbでない（Eabと略記）〉〈或るaはbでない（Oabと略記）〉という4種類の命題－－ここでa，bはなんらかの事物の集まり，集合を表すものとする－－が取り扱われている。それらの命題のおのおのにおけるaとbの関係は図1で表される。

　いま，P₁，……，P_nを前提命題（n≧1）としQを結論命題とする推論を，〈P₁，……，P_n⇒Q〉で表すものとすれば，まず下記の推論の成立は図1から明らかである。

　（1）〈Aab⇒Iab〉， 〈Eab⇒Oab〉

　（2）〈Eab⇒Eba〉， 〈Iab⇒Iba〉

また，例えば〈Aba，Acb⇒Aca〉や〈Eab，Icb⇒Oca〉は正しい推論であり，〈Aba，Ebc⇒Eca〉は成立しない推論である，ということは図2から明らかである。

　さて，A，I，E，Oの中の任意のものをX，Y，Zで表すと（したがってわれわれはXabによってAab，Iab，Eab，Oabの任意のどれかを表すことができる），三段論法とは下の（3）のいずれかの型に属する推論である，と定義される。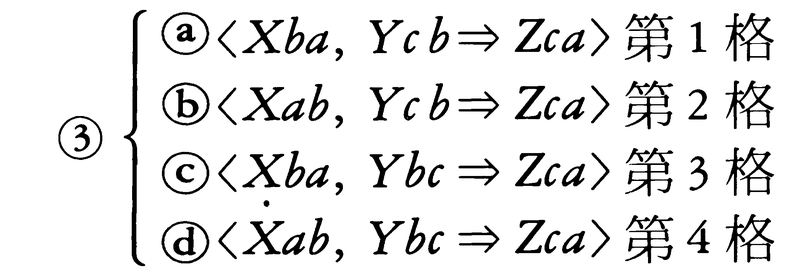

上の（a）（b）（c）（d）は順に〈第1格〉〈第2格〉〈第3格〉〈第4格〉の三段論法と呼ばれ，かつ，おのおのの格についてXYZの組は〈式〉と呼ばれている。例えば図2の三段論法は，（1）第1格AAA式，（2）第2格EIO式，（3）第3格AEE式となる。さて（3）において，結論命題Zcaの中の主語cは〈小名辞（小概念）minor term〉，述語aは〈大名辞（大概念）major term〉，推論においてcとaの仲立ちをするbは〈中名辞（中概念），媒名辞（媒概念）middle term〉と呼ばれる。また，前提命題のうち，大名辞を含む命題は〈大前提〉，小名辞を含む命題は〈小前提〉と呼ばれる。例えば，〈P₁“すべての動物は生物である”，P₂“すべての人間は動物である”⇒Q“すべての人間は生物である”〉という第1格AAA式の三段論法では，〈人間〉が小名辞，〈生物〉が大名辞，〈動物〉が中名辞であり，かつ，P₁が大前提，P₂が小前提である。

　さて，（3）のX，Y，ZのおのおのはA，I，E，Oの4通りでありうるから，一つの格について4×4×4＝64通りの式があり，かつ，格は四つであるから合計して，64×4＝256個の三段論法の型が存することになる。それらのうち成立する三段論法の格式が表の24個のみであることは，図2のごとき方法を用いて容易に確かめることができる（表のうち^＊印の式は，その直前の式の結論命題Zcaに上述の（1）を適用したものにすぎず－－例えば第1格AAAに〈Aca⇒Ica〉を適用すると第1格AAIが得られる－－いわば直前の式に内含されており，特に取り上げる必要のない格式であるとも言える）。かっこ内のラテン語名（^＊印以外のすべてにつけられている）は，古くから用いられている略称である。以上の（3），表は，正確には〈定言的三段論法〉と呼ばれ，次の（4），（5），（6）とは区別されている（以下において，p，q，rは任意の命題を表すものとする）。

　（4）〈“pならばq”，“qならばr”⇒“pならばr”〉という型の推論は〈純粋仮言三段論法〉，〈“pならばq”，“p”⇒“q”〉は〈仮言三段論法〉の〈肯定式〉，〈“pならばq”，“qでない”⇒“pでない”〉は同論法の〈否定式〉と呼ばれている。

　（5）〈“pとqのどちらか一方だけ成立する”，“qでない”⇒“p”〉は〈選言三段論法〉の〈否定肯定式〉，〈“pとqのどちらか一方だけ成立する”，“p”⇒“qでない”〉は同論法の〈肯定否定式〉と呼ばれる。

　（6）このほかに，〈仮言選言三段論法〉と呼ばれる推論の型があり，〈“pならばr，かつ，qならばrである”，“pとqのどちらか一方だけ成立する”⇒“r”〉はその一例である。

　現代論理学の立場から三段論法をとらえなおすとき，まず，定言的三段論法（3）を構成する各命題は述語論理の式として通常つぎのように解釈される。

　Aab⇔≏x（a（x）⊃b（x））

　Iab⇔≐x（a（x）∧b（x））

　Eab⇔≏x（a（x）⊃～b（x））

　Oab⇔≐x（a（x）∧～b（x））

この解釈によれば，例えば上述（1）の推論はaが空集合のとき，すなわち～≐x（a（x））が真のとき不成立となる。同様にa，b，cが空集合の場合を検討すると，表のうち第1格AAI，EAO，第2格EAO，AEO，第3格AAI，EAO，第4格AAI，AEO，EAOが不成立であることがわかる。しかし，伝統的論理学においては〈推論は常に存在する事物に関してなされる〉という暗黙の前提（これを〈存在仮定existential import〉と呼ぶ）が存すると解されるから，≐x（a（x）），≐x（b（x）），≐x（c（x））を推論の前提命題として付加すれば，（1）と表のすべてが成立することになる。また，（4），（5），（6）の三段論法は，現代の命題論理におけるトートロジーの一部であると解釈されている。
→判断　→論理学
執筆者：岡部 満

インド

ニヤーヤ学派，バイシェーシカ学派は，〈他人のための推理〉（論証）に，五つの文からなる論式（五分作法）を用いる。例えば，主張〈かの山に火あり〉，理由〈煙の故に〉，実例〈およそ煙あるところには火あり。かまどのごとし〉，適用〈この山においてもしかり〉，結論〈故にしかり〉となる。ただ，実際には，これを略して，主張，理由，実例の三つだけを用いることが多い。これにたいし，ディグナーガ（陳那，6世紀）以降の仏教論理学は，前三文ないし後三文のみで十分であるとし，〈三支作法〉（ないし，主張・結論を除いた〈二支作法〉）を主張した。いわゆる〈三段論法〉とたしかに外見上は似ているが，西洋論理学が概念の外延間の関係に主眼をおくのにたいし，インドの論理学は，基体（例えば山）と属性（火，煙）との関係に着目して分析を行う点に大きな違いがあると言える。
執筆者：宮元 啓一

図1～図2，表

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

三段論法
さんだんろんぽう

二つの前提から一つの結論を導く論理的推論のこと。間接推理を含む。前提の連言から結論への含意であるといってもよい。ただし、前提も結論も、二つの項が結合されてできた命題である。たとえば、「すべての動物は生物である」「すべての人間は動物である」という二つの前提から、「すべての人間は生物である」という結論を得る推論は典型的な三段論法である。この例から明らかなように、ここでいう項は、人間、動物、生物といった概念、すなわち普遍的な何かを表していると考えられる。

　さて、アリストテレスにまでさかのぼることのできる、いわゆるアリストテレス式三段論法においては、項と項の結合には四つの種類がある。すなわち、全称肯定判断、全称否定判断、特称肯定判断、特称否定判断の四つである。これらは、西洋中世の伝統に従って、A判断、E判断、I判断、O判断とよばれる。そして、それぞれ、「すべてのAはBである」、「すべてのAはBでない」、「あるAはBである」、「あるAはBでない」という形で表される。これから明らかなように、三段論法は、基本的には、自然言語の論理である。

　さて、三段論法は、中概念の位置によって、

という四つの格に分類される。ただし、P、M、Sは、それぞれ、大概念、中概念、小概念といわれる。

　三段論法を構成する三つの命題は、先にあげた4種類の判断のいずれでもよいから、つごう256通りの三段論法が可能である。しかし、アリストテレス式三段論法では、24通りが妥当であるにすぎない。アリストテレス以来、イスラム文化圏、西洋中世を通じて、三段論法に関しては多くの研究が積み重ねられてきたが、その後、19世紀末に出現した、数学の基礎づけを目的とする近代論理学の陰に隠れて、三段論法はかつての魅力を失ってしまった。しかし、最近では、近代論理学と結び付き、三段論法の研究はふたたび活発になり始めている。

　インドにおいても、アリストテレス式三段論法とは異なった形の三段論法が、現在まで2000年にわたって研究されてきた。

［石本　新］

『Jan LukasiewiczAristotle's Syllogistic from the Standpoint of Modern Formal Logic, 2nd ed. (1957, Oxford University Press, London)』

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

三段論法【さんだんろんぽう】

〈すべての人間は死す。ソクラテスは人間である。ゆえにソクラテスは死す〉のように，二つの前提から一つの結論を導き出す間接推理。アリストテレスによって定式化され，中世を通じて洗練された伝統的論理学の主要部門。結論の主語を小概念，述語を大概念，両前提を媒介する概念（人間）を媒概念または中概念，大概念を含む前提を大前提，小概念を含む前提を小前提という。三つの命題が定言的命題からなるものを定言的三段論法，前提に仮言的命題または選言的命題を含むものを仮言的三段論法または選言的三段論法という。
→関連項目演繹｜オルガノン｜還元（哲学）｜記号論理学｜推理｜両刀論法

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

三段論法
さんだんろんぽう
syllogismus

前提となる2個の判断と結論としての判断より成る推論法で，アリストテレスにより基礎がおかれた。その前提の性格に従い，(1) 定言的判断，(2) 仮言的判断，(3) 選言的判断に区別され，次のように定式化される。 (1) いかなるqもrでない。しかるにpはq。ゆえにpはrでない。 (2) もしもpならばq，もしqならr，ゆえにもしpならばr。 (3) pあるいはqのいずれかが成り立つ。しかるにpではない。ゆえにqである。ギリシア語の syllogismosという語は，プラトンやアリストテレスではただ議論を意味する場合もあったが，後者は syllogismosをある事柄が前提されたとき，ほかの事柄がそこから必然的に導き出される推論であると定義し，多くの場合定言的判断の意に用いた。

出典　ブリタニカ国際大百科事典 小項目事典

四字熟語を知る辞典

三段論法

二つの前提命題から一つの結論命題を導く論理的推理をいう。たとえば、「すべての人間は動物である」「A氏は人間である」「故にA氏は動物である」とする推論の類。

[使用例] 一層奇抜な其質問は立派に三段論法の形式を具えていた［夏目漱石＊明暗｜1916］

[使用例] 機智とは三段論法を欠いた思想であり［芥川龍之介＊侏儒の言葉｜1923～27］

出典　四字熟語を知る辞典

世界大百科事典（旧版）内の三段論法の言及

【アリストテレス】より

…
［思想］
　アリストテレスの思考の大きな特徴の一つに，言葉の多義性に注目した分析の精密さがあげられる。彼は〈名辞〉〈述語〉〈命題〉などといった根本概念を確定したうえで史上初めて三段論法の定式化をなしとげ，その後の論理学の基礎をきずいた。彼は自身の説を展開する際に彼以前の哲学者の説を紹介･批判することが多いが，彼の創始した多数の用語･概念は，その場合にも威力を発揮する。…

【機械推論】より

…　上の規則が知識ベースに蓄えられていて，さらに〈肉がある〉〈タマネギがある〉〈ジャガイモがある〉〈ニンジンがある〉〈カレー粉がある〉という事実が知識ベースに書かれていれば,〈カレーができる〉ということが推論できる。　これは，三段論法と呼ばれる以下の推論規則　　前提1　AならばBである　　前提2　Aである　　────────────　　結論　Bであるを用いた結論の導出であり，いつでも正しい結論が得られることが論理的に保証されている。　さらに変数や関数を含んだ関係を表すことのできる一階述語論理や，可能性を表現することのできる様相論理と呼ばれる論理もある。…

【様相論理学】より

…〈必然的〉〈可能的〉といった様相概念を形式的に取り扱う論理学。様相三段論法という形において，アリストテレスがすでに様相論理学の研究に手をそめていたことは注目に値する。その後，西洋古代，中世においても様相論理学はアリストテレスの伝統に基づいて，散発的ではあるが，研究されてきた。…

【ルカシエービチ】より

…第2次大戦後はダブリンで研究。多値論理を含む命題論理，三段論法の現代的定式化，さらにそれと密接に結びついている論理学史の分野で多くの先駆的業績を残した。主著に《数学的論理学要説》(1929)，《現代形式論理学の観点より見たアリストテレスの三段論法》(1951)がある。…

【論理学】より

…例えば，集合に含まれる〈もの〉を顧慮しないで，集合相互の関係を考察する論理学は集合算と呼ばれる。アリストテレスが樹立した無様相三段論法の体系は，集合算のなかに吸収される。〈もの〉として命題だけを考え，命題が属する2種類の集合――真な命題の集合と偽な命題の集合――を考え，その間の関係を考察する論理学は命題論理学と呼ばれる。…

※「三段論法」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」