中国数学（読み）ちゅうごくすうがく

改訂新版　世界大百科事典

中国数学 (ちゅうごくすうがく)

中国で文字による記録が残っているのは，殷代晩期の甲骨文からである。甲骨文による記数法は十進法が主体で，万位までを数えている。このほか十干十二支を組み合わせた六十進法で日を数えている。次の周代の数学を知る資料は乏しいが，春秋戦国ともなると，四則計算を中心にかなり数学が発達してきたと思われる。漢字による数字表記では，現在のアラビア数字とはちがい，筆算が行えないため，計算には算木（算，籌（ちゆう），策などという）が使用された。大きさや形は一定しないが，竹や木を短く切った棒を格子状に区切った盤に並べて（布算という）数字を表し，計算を行った。布算には縦式と横式とがあり，縦式は一，百，万位などの数を，横式は十，千位などの数を表した。

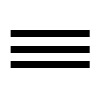
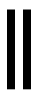
両者を交互に置き，例えば3256は，算木を盤上の格子目に というように置いた。零の表示はなく，格子の場所を空けたままにした。

漢より唐へ

ギリシア数学といえばユークリッド幾何学で代表されるが，中国ではこうした論証的幾何学はまったく発達しなかった。もちろん平面や立体が取り扱われたが，その場合面積や体積を求めることが中心で，あくまで実用を重んじた。早くから官僚制度が発達した中国では，行政上の必要と結びついて数学が発達したといえよう。漢代に成立した《九章算術》は古代数学を代表する著述で，租税，輸送，土木など行政上必要な計算例を網羅している。問題はすべて具体的な数字で与えられているが，かなり程度の高いもので，各種の平面や立体を取り扱うほか，多元一次方程式や一元二次方程式，ピタゴラスの定理の応用などが含まれる。方程式の計算には負数が取り扱われている。また約分についてはユークリッドの方法が述べられている。3世紀半ばの魏の劉徽はこの書に対しすぐれた注釈を書いたが，その中で円周率の計算を論じ，近似値として3.1416を得ている。漢・唐の間の数学書としては《九章算術》を含む〈十部算経〉《算経十書》があるが，この中の《綴術》を書いた劉宋（420-479）の祖沖之は円周率を研究し，密率として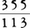 ， 約率として22/7を求めた。この密率の値がヨーロッパで知られたのは16世紀になってからである。なおその子の祖之は球の体積計算に成功した。隋の時代には劉焯（りゆうしやく）が天文計算にはじめて補間法を使用した。次の唐代にはインド人天文学者瞿曇悉達（くどんしつた）が《九執暦》を編集し，その中でアラビア数字の源流であるインド数字，それに加えて正弦関数を紹介したが，中国数学に影響を与えることはできなかった。中国人の外来文化に対するきびしい拒否反応を示すものといえよう。なお唐代には数学に詳しい官吏を養成するための学校〈算学〉が設けられ，《算経十書》が教科書に使用された。この場合試験問題はすべて教科書から出題される状態で，〈算学〉は必ずしもすぐれた数学者を養成する機関ではなかった。

宋・元・明の数学

宋代にも一時的に〈算学〉が設けられたが，とくに注目すべきことは，印刷術の流行にともない，すでに散逸した《綴術》を除く古算書が〈算学〉を中心に印刷され，このことが数学知識の普及に役立ったことである。12世紀の初頭に北宋の都は金に攻略され，宋は江南に移って南宋となった。この金も1234年にモンゴルの軍隊に滅ぼされ，少しおくれて南宋を滅ぼしたモンゴルは国号を元と称した。この金・元交替のころ，華北を中心に新しい数学が興った。かつて金に仕えた李冶の《測円海鏡》（1248）に紹介された〈天元術〉がそれで，一種の代数術である。現在の代数学で〈未知数をxとする〉というのに対し，〈天元の一を立てる〉といい，〈元〉字を数字の横に記し，任意の次数の方程式を表示するのである。例えば25x²＋280x－6905を表示するのに，算木を次のように置いた。

　　　25

　　280元

　－6905

元字の横は未知数一次の係数，その上は二次の係数，下は常数を表した。こうして未知数を含む方程式の計算が行われたのである。なお李冶には《益古演段》（1259）の著述がある。元の時代になって朱世傑が書いた《算学啓蒙》はやはり天元術を紹介しているが，江戸時代の数学者にもてはやされ，和算の発達に大きな貢献をした。朱世傑はまた《四元玉鑑》（1303）を著し，四元による計算法を説いたが，この書には級数の和を求める問題が多く含まれ，また（a＋b）ⁿを展開した時の係数を表示した図がある。これは17世紀のフランス人哲学者パスカルにちなんで〈パスカルの三角形〉と呼ばれるものに一致する。

　南宋治下の数学者には，秦九韶および楊輝が有名である。秦九韶は《数書九章》（1247）を著したが，そこに説かれた〈大衍求一術〉は不定方程式を論じたものである。中国では早くから数字方程式の解法が研究されてきたが，《数書九章》の〈正負開方術〉にいたって，19世紀初頭のイギリス人数学者W.G.ホーナーの方法と一致する方法が完成され，十次方程式が解かれている。またこの書には零を小円で表すことが行われている。いま1人の楊輝は民間の数学者であり，多くの数学書を書いたが，そのいくつかを集めたものに《楊輝算法》がある。これに含まれる《続古摘奇算法》は各種の〈方陣〉（魔方陣）を図示しており，江戸時代の関孝和がそれを学んだ。

　計算器として現在も盛んに使用される〈そろばん〉は南宋のころから流行したと思われ，同じころから庶民の勃興を背景として庶民数学がしだいに発達するようになった。楊輝もそうした数学書を書いている。元の郭守敬によって造られたとされる〈授時暦〉にはピタゴラスの定理を応用して球面三角形の問題を解いている。また元の時代にはイスラム諸国を通じてアラビア数字が伝わったこともある。しかし元の時代から明代を通じて，南宋に始まった庶民数学は一段と隆盛となった。ことに明代には栄敬の《九章算法比数大全》（1450）や程大位の《算法統宗》（1592）などが著された。いずれも《九章算術》に範をとって，伝統数学の範囲でかなり広く諸問題をとりあげている。

　もちろんその中には西方伝来の数学も含まれる。インドに起こりイスラム諸国に伝わった一種の機械的乗法が〈写算〉（矣数）または〈舗地錦〉（程大位）の名で紹介されている。この方法はまたヨーロッパに伝わり，15～16世紀のころに流行したが，明・清の間にはヨーロッパを通じて再輸入され，この場合には〈籌算（ちゆうさん）〉の名で知られた。

　程大位の《算法統宗》全17巻は庶民数学を代表する著述で，ことにその第2巻には〈そろばん〉の計算法を詳説している。刊行以来たびたび版を重ね，また多数の異版が出版され，清朝時代になっても広く読まれた。江戸時代に吉田光由はこの書に倣って《塵劫記》を著したが，やはり重版，異版が数多く出版された。

明末から清朝へ

16世紀の初めからポルトガル船が中国に来航するようになり，ポルトガル船に乗ってキリスト教布教にやってきたイエズス会士がヨーロッパの天文学や数学を紹介した。唐代のインド数学，元代のイスラム数学の場合とちがって，ヨーロッパ数学はかなり根を下ろしたが，アラビア数字はもちろん，数式などもヨーロッパ風のものは採用されずに終わった。1582年（万暦10）に来たマテオ・リッチ（漢名，利瑪竇）は開明的な高官徐光啓の助力を得て，ユークリッド幾何学書《ストイケイア》の前半の6巻を《幾何原本》として漢訳し，論証的幾何学を中国に紹介した。なお後半の9巻は清末に漢訳された。またマテオ・リッチは李之藻の助力によってヨーロッパの算術書《同文算指》を漢訳した。徐光啓は西洋天文学に基づいて改暦を行うことを計画し，そのために必要なヨーロッパ天文学の一大叢書《崇禎暦書》を，アダム・シャール（湯若望）らの助力で完成した（1634・崇禎7）。この叢書には数学書が含まれており，《大測》は平面三角法，《測量全義》にはさらに球面三角法が併せて取り上げられた。また後者には三角関数表がある。三角関数表については別に《割円句股八線表》がある。

　清朝の初期にもイエズス会士によるヨーロッパ数学の輸入はつづき，まず対数が紹介された。また康煕帝の末年に編集された《数理精蘊》にはヨーロッパの代数学が〈借根方〉の名で初めて紹介された。康煕帝の時代には清朝を代表する数学者梅文鼎が活躍し，伝統的な天文学・数学を研究するとともに，ヨーロッパのそれをよく消化した。彼の著書は1723年（雍正1）に《暦算全書》として刊行されたが，これには中国・西洋の暦算学がよく折衷されている。梅文鼎の著作は別に孫の梅成の手で1761年（乾隆26）に《梅氏叢書輯要》の名で刊行されているが，この中に〈杜氏の法〉というのがみえる。これはフランス人イエズス会士P.ジャルトゥ（杜徳美）が伝えたもので，円周率や三角関数を無限級数に展開したものである。この展開式はのちにモンゴル人数学者明安図（1700?-70）によって研究され，《割円密率捷法》（1774）の名で出版された。これは清朝における中国人の数学的業績を代表するものといわれている。

　康煕帝の時代に盛んであったヨーロッパ科学の輸入も，雍正・乾隆の時代にキリスト教への弾圧が強まるとともに衰微した。乾隆帝の時代に中国古典を整理する〈四庫全書館〉が創設されるにおよんで，古典数学の研究が盛んとなった。《算経十書》が再発見され，李冶，朱世傑などの天元術に関する研究が流行するようになった。また暦算学者の列伝である《疇人伝》（1799）が阮元の下で編集された。19世紀に入って焦循，汪萊，李鋭などによってやや独創的な研究が行われたが，ヨーロッパ数学とのへだたりは大きくなるばかりであった。1840年（道光20）にアヘン戦争が起こり，やがてプロテスタント宣教師が中国に来るようになり，イギリス人宣教師A.ワイリー（漢名，偉烈亜力）やJ.フライヤー（傅蘭雅）などが新しい数学の紹介に努めた。これには中国人の李善蘭や華蘅芳が協力した。しかし宣教師はもちろん数学の専門家ではなく，漢訳書も程度の高いものではなかった。中国人の手で新しい近代数学の研究が始まるのは，中華民国時代以降のことである。
執筆者：藪内 清

出典　株式会社平凡社「改訂新版　世界大百科事典」