補間法（読み）ホカンホウ（英語表記）interpolation

デジタル大辞泉

ほかん‐ほう〔‐ハフ〕【補間法】

数学で、関数において、二つ以上の点での関数値が知られているとき、その間の任意の点に対する関数値あるいは近似値を求める方法。内挿法。→補外法

出典　小学館

精選版 日本国語大辞典

ほかん‐ほう‥ハフ【補間法】

1. 〘 名詞 〙 関数の、二つ以上の変数の値に対する関数値を知って、それらの間の任意の変数の値に対する関数値ないしはその近似値を求める計算法。内挿法。⇔逆補間法。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

補間法 (ほかんほう)
interpolation

例えば対数表や三角関数表のような関数値の表は，xのとびとびの値x₀，x₁，x₂，……に対する関数f（x）の値f₀，f₁，f₂，……が与えられているから，表に与えられていない中間の値xに対するf（x）の値を求める必要が起こる。また，実験や観測で得られた測定値から，測定しなかった点での値を推定する場合も，同様な問題が起こる。このように，知られた関数値から，それらの中間の関数値を近似的に求める方法を補間法（または内挿法）という。

　もっとも簡単な補間法は線形補間（または比例部分）と呼ばれるものである。それは例えばf₀＝f（x₀），f₁＝f（x₁）の値を知ってx₀＜x＜x₁なるxに対するf（x）を求めるのに，区間［x₀，x₁］ではf（x）が近似的に一次式で表されると考えて，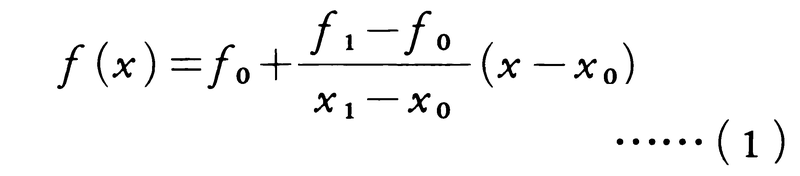

とするのである。これは関数y＝f（x）のグラフが図の曲線のような場合に，xの値x₀，x₁に対応するグラフ上の点A，Bを直線で結び，xに対応するx軸上の点，グラフ上の点，線分AB上の点をそれぞれP，Q，Cとするとき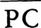，をf（x）の値PQの近似値とみなすことである。

　ふつうの対数表や，三角関数表などでは，x₀，x₁，x₂，……の刻みが十分細かくとってあるので，図の 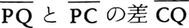は（図では誇張して描かれているが）無視できるほど小さい（実際にその誤差はたいていは数表の末尾の桁における四捨五入などによる誤差よりも小さい）ので，実用上はこの方法がよく用いられる。

　線形補間よりも近似をよくするには，f（x）がxのn次多項式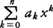で表されるものと考える。関数値が与えられている点x_iのうちでxに近いn＋1個の点x₀，x₁，……，x_n（以後つねにx₀＜x₁＜……＜x_nとしておく）を選び，それらの点における関数値f₀，f₁，……，f_nを用いて，

　f（x_i）＝f_i （i＝0，1，……，n）　　　……（2）　

という条件のもとで多項式f（x）を定めると，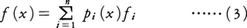

ここでp_i（x）は次の多項式である。

（3）をラグランジュの補間公式という。

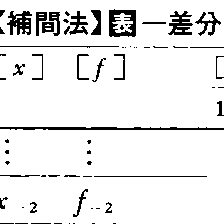
　ふつうの関数表では変数……，x₀，x₁，x₂，……は等間隔に配置されている。このときには，階差表を使って次のように計算される。まず関数値f_i＝f（x_i）の1階差分⊿_if≡⊿_i¹f＝f_i+1－f_i，2階差分⊿_i²f＝⊿_i+1¹f－⊿_i¹f，……，一般にn階差分⊿_iⁿf＝⊿_i+1ⁿ⁻¹f－⊿_iⁿ⁻¹fを逐次定義する。これらを表のように関数値の隣に差分を順次並べて書くと，わかりやすい。このような表を差分表または階差表という。この表では差分⊿_iⁿfを単に⊿_iⁿと書いた。以下の式においても同様に略記する。

　変数の間隔x_i+1－x_iをhとするとき，この表を使って，x₀とx₁との間の値x₀＋ph（0＜p＜1）に対するfの値を与える次のような公式が知られている。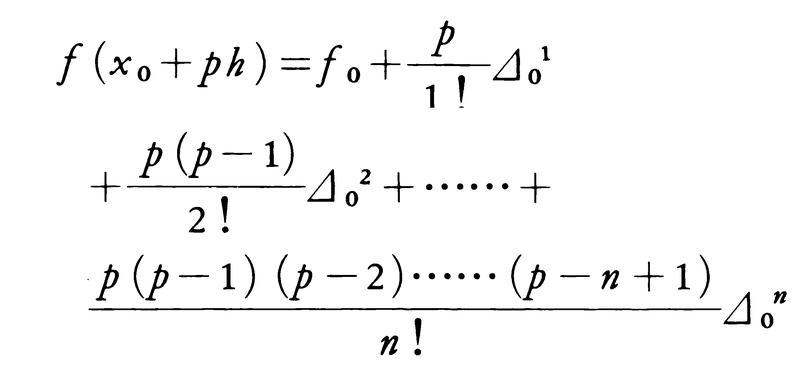

これをグレゴリー=ニュートンの公式（単にニュートンの補間公式ともいう）という。

　また，

　　q＝1－pとして，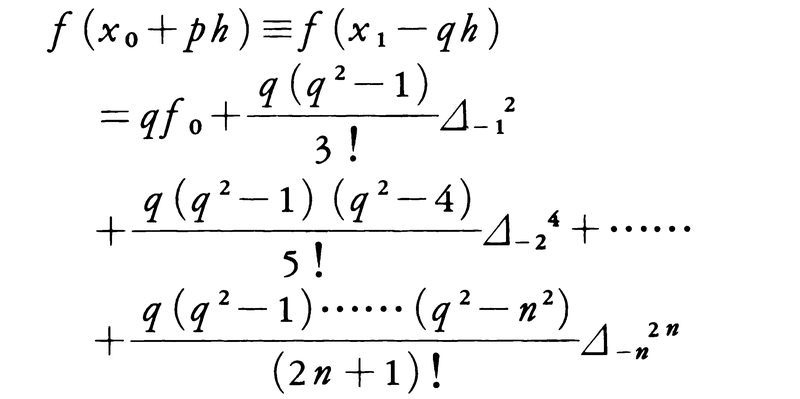



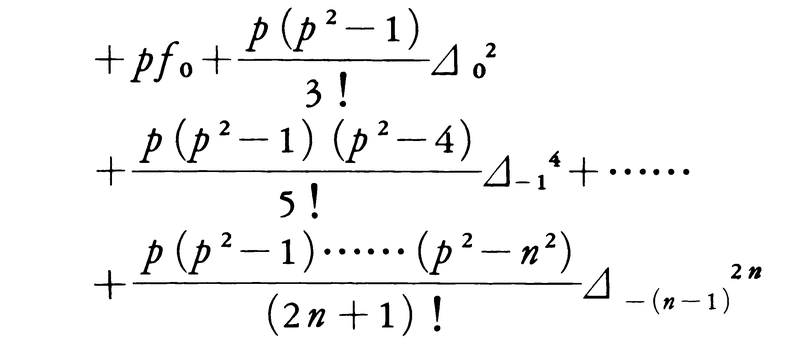
これをエベレットJ.D.Everettの補間公式という。

　ふつうの補間法とは反対に，fの値を与えてxの値を求めることを逆補間という。対数表や三角関数表の例でいうと，log₁₀xあるいはsinxの値を与えてxを求める場合である。xとfの役目を交換すると，ふつうの補間法とまったく同じであるが，通常の数表ではx_iは等間隔であるのに対して，逆補間では一般に不等間隔の場合を問題にしなければならない。また，本項目の最初に述べた実験や観測の測定値からの補間法も，一般には不等間隔の場合である。

　不等間隔の場合の補間法でも，線形補間は等間隔の場合と同じであるが，一般の補間法では，前述の階差表を用いる方法はそのままでは適用されない。この場合には差分商による方法が用いられる。x_iに対する関数値を前のようにf_iとして，

を逐次定義する（添字i，j，k，……はすべて相異なるものとする）。前述の各階の差分商は添字に関して対称性をもっており，例えばf₀₁……_kは次のように表される。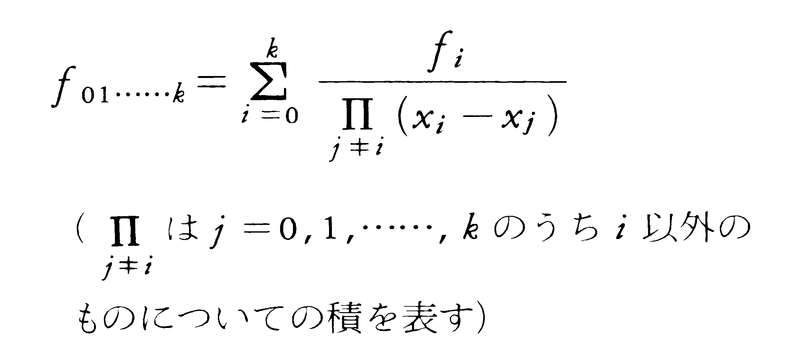

差分商を用いて，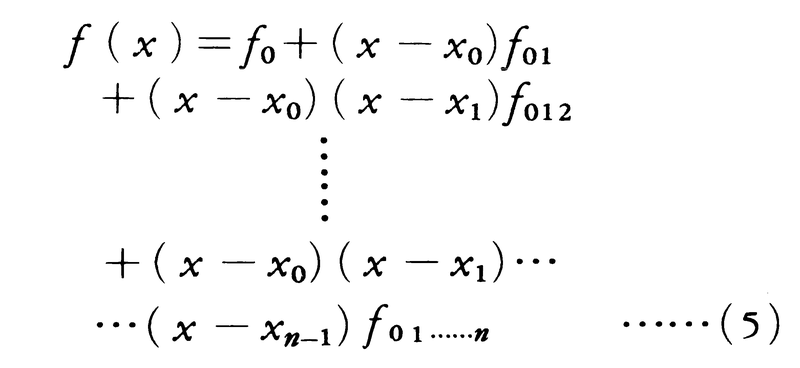

とすると，これは条件（2）を満たすn次多項式であるから，補間公式として用いられ，これをニュートンの補間公式という。（5）でf_ijなどを書き直せばラグランジュの補間公式（3）そのものになるが，差分商を逐次計算して（5）に代入するのが実用上便利である。

　補間法はその名のとおり，未知の関数値f（x）に対するxが，関数値の与えられているx₀，x₁，……，x_n（x₀＜x₁＜……＜x_n）の間にある場合に，f（x）の近似計算をする方法であるが，xがx₀よりもわずかに小さいとき，またはx_nよりもわずかに大きいときも，同様な公式で関数値の近似計算ができる。この場合を補外法（または外挿法）と呼ぶことがある。
執筆者：伊藤 清三

図－線形補間

表－差分表

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

補間法
ほかんほう
interpolation method

数表に出ている値の間を補うこと、すなわち、いくつかの点で与えられている関数値を基に、それらの点の中間における関数値を求めることをいう。

　もっとも簡単な補間法は、隣り合った2点間を一次式で補間する線形補間で、これは、いわば折れ線グラフで近似するやり方である。

　同様に、3点を通る二次式を用いる方法、4点を通る三次式を用いる方法などの高次補間を考えることができる。一般にn点
　　(x₁,y₁),(x₂,y₂),……,(x_n,y_n)
を通るn－1次式は次のように表せる。

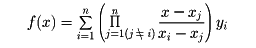
これをラグランジュの補間多項式という。これは不等間隔分点でも適用できるが、とくに等間隔分点の場合には、階差表を用いると計算が簡単になる。この種の公式としては、ニュートン、ガウス、ベッセル、スターリング、エベレットなどの名を冠した公式がある。

　補間多項式の次数をむやみにあげても精度はかならずしもよくならず、むしろ悪い結果をもたらすことが多い。とくに、数値微分といって、補間多項式を微分することによって近似的な微分係数を求めようとする場合、次数をあげると失敗することが多い。その理由は、データの誤差が補間の過程で拡大されるためでもあるが、たとえデータに誤差がまったくなくても異常な結果になることがある。

［戸川隼人］

スプライン補間

スプラインsplineとは自在定規のことで、自在定規のように、いくつかの与えられた点を通る滑らかな曲線を描くための補間関数として考案されたのがスプライン関数である。コンピュータによる図形表示や、工作機械の数値制御などに用いられる。

［戸川隼人］

『P・ヘンリッチ著、一松信・平本巌・本田勝訳『数値解析の基礎』（1973・培風館）』▽『市田浩三・吉本富士市著『スプライン関数とその応用』（1979・教育出版）』▽『戸川隼人著『数値計算法』（1981・コロナ社）』▽『杉原正顕・室田一雄著『数値計算法の数理』（1994・岩波書店）』▽『名取亮編、長谷川秀彦他著『数値計算法』（1998・オーム社）』▽『二宮市三編、吉田年雄他著『数値計算のつぼ』（2004・共立出版）』

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

補間法
ほかんほう
interpolation

変数 x の関数 f(x) の形は未知であるが，ある間隔をおいた2つ以上の変数の値 x₁，x₂，…，x_n に対する関数の値 f(x₁)，f(x₂)，…，f(x_n) がわかっている場合，x₁ と x_n の間にある任意の x に対応する f(x) の値の近似値を求める方法を，補間法，または内挿法という。上の場合，x₁ と x_n の外側にある任意の x に対する f(x) の値の近似値を求める方法を，補外法，または外挿法 extrapolationという。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

補間法【ほかんほう】

変数xの関数f（x）のx₁，x₂，…，x(/n)における値f（x₁），f（x₂），…，f（x(/n)）が知られているとき，それらを用いて他のxに対するf（x）の値を求めること。xの値がx₁，…，x(/n)の最大値と最小値の間にあるときは内挿法，その外にあるときは外挿法または補外法と呼ぶ。

出典　株式会社平凡社

会計用語キーワード辞典

補間法

投資案の内部収益率を算出する方法のひとつです。投資案の内部収益率をより正確に出すために、ある狭い範囲の中では割引率の変化と年金原価係数の変化の比率は一定であると仮定して算出する方法をいいます。

出典　（株）シクミカ：運営「会計用語キーワード辞典」