分散分析（読み）ブンサンブンセキ（その他表記）analysis of variance（ANOVA）

デジタル大辞泉

ぶんさん‐ぶんせき【分散分析】

観測されたデータのばらつきを、さまざまな要因の効果による変動と誤差による変動に分離し、主要因を明らかにして、その効果の大きさを推定する統計学的手法の一。英国の統計学者R＝A＝フィッシャーが確立。

出典　小学館

改訂新版　世界大百科事典

分散分析 (ぶんさんぶんせき)
analysis of variance（ANOVA）

一つの特性についてのデータのばらつきの大きさを，そのばらつきの要因別に分解することにより重要な要因を明らかにし，その影響の強さを知るための統計的方法の一つ。たとえば，米などの農作物の収量は，その品種，天候，土壌の性質，肥料の使い方などの影響を受ける。工業製品のできばえの特性は，原材料，作業者，製造機械，製造法などのそれぞれの違いによってばらついてくる。このようなばらつきの要因と考えられるもの（米の収量の場合には品種，天候，土壌，肥料など）を因子といい，一つの因子の中で取り上げる区別（品種の場合には個々の品種）を水準という。分散分析法は農事試験場での実験データの解析方法として発展し，その後広い分野で応用されるようになっている。真の要因を発見するためには実験計画法に基づいて因子間の水準の組合せのつりあいをとって実験を実施することが望ましい。たとえば，機械AとBによる製品寸法精度の違いを調べるのに，作業者アが機械Aを，作業者イが機械Bを常に操作してデータをとったのでは，機械の違いか作業者の違いかが分離できない（このような状況を一般に2因子の交絡という）。

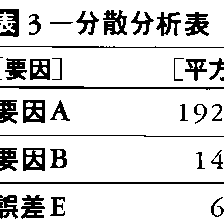
　分散分析をするデータは1因子のときは表1，2因子のときは表2のように整理され，それぞれ1元（配置）データ，2元（配置）データといわれることがある。この種の簡単な形式の場合のデータは日常的にもしばしば観察され，分散分析の方法を応用して解析し要因の影響を検討することができる。ただし，考慮に入れていない要因が存在して交絡している可能性にも配慮することが必要である。分散分析の結果は表3のような分散分析表としてまとめられる。そこで，データ全体のばらつきは各データの総平均値からの差の2乗の和，すなわち平方和ではかられ，表3の平方和の欄のように，その平方和が要因別に分解される。要因別の平方和は，その要因の水準別にデータを分けて水準別の平均値を求め，その間のばらつきとしてとらえられる。取り上げた要因で説明し尽くせない残りの平方和は，制御できない統計的誤差によるものと考えられる。その誤差による平方和に対して，各要因による平方和の大きさを不偏分散の比によって比較し，各要因の影響の強さが統計的に推測される。要因の影響が強いということは，もとのデータのばらつきにその要因が寄与していること，言い換えれば，稲の品種によって収量に大きい差が出るように，その要因の水準の違いによって目的とするデータの値が大きく異なってくることを意味する。さらに，分散分析法では，各データを，

　総平均＋使用した水準の効果＋誤差

の形に分解することができ，どの水準の組合せがよいか，誤差に異常のあるものはないかなどの問題を統計的に検討することができる。
執筆者：吉沢 正

表1～表2

表3－分散分析表

出典　株式会社平凡社「改訂新版　世界大百科事典」

岩石学辞典

分散分析

分散分析は測定値全体の変動を様々な要因に基づく変動に分解する方法で，この分解は平方和の形で進められる．測定値は総平均と変動部分と誤差に分解され，変動は不偏分散を用い，変動部分と誤差部分の二つの分散比を計算し，F分布表を用いて検定する．何種類かの質的に異なる処理の効果を比較する問題に適切な方法である．二つの平均値の比較にはt検定を用いるが，多くの標本の平均値を比較する場合にはフィッシャーによるF検定が用いられる［Griffiths : 1967, Koch & Link : 1971］．

出典　朝倉書店

ブリタニカ国際大百科事典 小項目事典

分散分析
ぶんさんぶんせき
analysis of variance

標準的な統計分析法の一つ。多くの因子の作用する状況下で測定したデータの変動を，各因子に起因する変動および誤差に起因する変動の和に分解し，その寄与の大きい因子はきいていると統計的推論を行う。イギリスの統計学者 R. A.フィッシャーが農事試験に用いた実験計画のデータの分析に用いて以来，心理学，工学などのきわめて広い分野で使われている。

出典　ブリタニカ国際大百科事典 小項目事典

栄養・生化学辞典

分散分析

　一群のデータの解析手法で，データの分散を変動の因子や個体間の誤差などの要因に分けて解析する統計学的な方法．

出典　朝倉書店

ブランド用語集

分散分析

分散分析とは複数（通常3以上）のグループ間で平均値を比較するための手法のことをいう。

出典　(株)トライベック・ブランド戦略研究所