区分求積法（読み）クブンキュウセキホウ（英語表記）mensuration by division

デジタル大辞泉

くぶんきゅうせき‐ほう〔クブンキウセキハフ〕【区分求積法】

図形を細かく分けて、各区分の面積または体積を求め、それらの和から全体の面積または体積を近似的に求める方法。

出典　小学館

精選版 日本国語大辞典

くぶん‐きゅうせきほう‥キウセキハフ【区分求積法】

1. 〘 名詞 〙 平面図形の面積や立体の体積を求める方法の一つ。問題の図形や立体を、面積や体積の求めやすい小さな多角形や立体の和集合で近似し、その面積や体積の極限値として、問題の図形の面積や立体の体積を算出する。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

区分求積法 (くぶんきゅうせきほう)
mensuration by division

曲線で囲まれた平面図形の面積Sの求め方を考えてみよう（図1）。まず，図形を内部に含む一つの正方形を描き，この正方形の縦，横をそれぞれn等分して方眼を描く。このとき，図形の内部に完全に含まれるすべての小正方形の面積の和をs_n，図形と共通点があるようなすべての小正方形の面積の和をS_nとすると，s_n＜S＜S_nである。ここでnをしだいに大きくして正方形の分割を細かくしていくと，s_nはしだいに増大し，S_nはしだいに減少して，それぞれ図形の内側と外側からSをより精密に近似する。そして，nを限りなく大きくしたときの極限値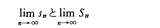，とが一致するならば，その値が求める図形の面積Sに等しいはずである。

　このように，与えられた図形の面積や体積を求めるのに，（1）微小な基本図形の集りを作って，その図形を近似する図形を考え，（2）その近似図形の面積や体積の極限値を計算する，という方法がある。このような計算法を区分求積法という。

　例として，座標平面上の放物線y＝x²とx軸と直線x＝1とで囲まれた部分の面積Sを求めてみよう（図2，3）。

　区間0≦x≦1をn等分すると，各小区間の長さは1/nである。h＝1/nとおくと，各小区間の左端に対応する放物線上の点yの値は，左から0，h²，（2h）²，……，｛（n－1）h｝²であるから，図2において灰色部分の面積s_nは，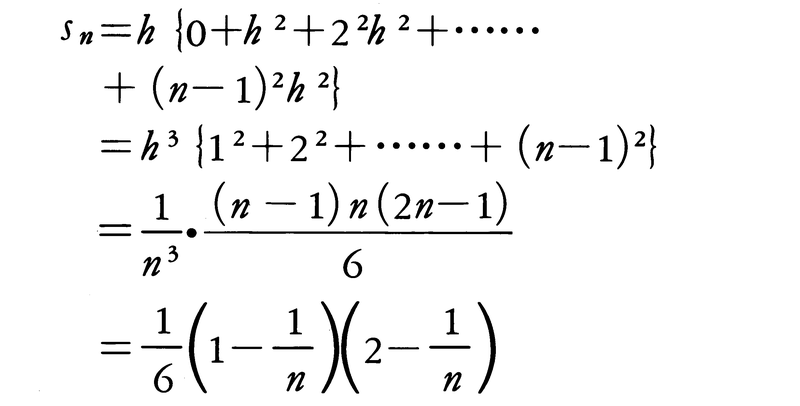

同様にして，図3の灰色部分の面積S_nは，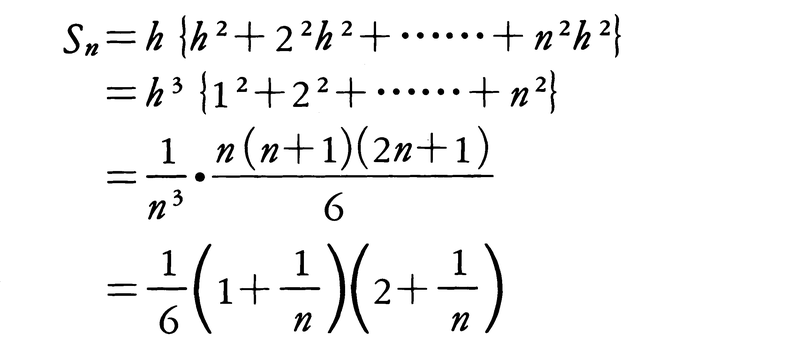

したがって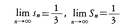，となるから，求める面積，である。一般に，いくつかの滑らかな曲線で囲まれた平面図形や，いくつかの滑らかな曲面で囲まれた立体図形に対しては，内部から近似した図形と外部から近似した図形の面積や体積は，極限において一致することが知られている。

　関数y＝f（x）のグラフが区間a≦x≦bにおいて一つの連続曲線であり，この区間ではf（x）＞0であるとき，上の例y＝x²の場合と同様にして，曲線y＝f（x）とx軸および2直線x＝a，x＝bで囲まれた部分の面積Sを求めることができる。このSの値を，記号で表し，関数f（x）のaからbまでの定積分という。個々の具体的な関数f（x）に対して上記の面積Sを求めるには，区分求積法によるよりも原始関数を用いるのがふつうであるが，考察の基礎としての区分求積法の考え方は重要である。
→積分
執筆者：伊藤 清三

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

区分求積法
くぶんきゅうせきほう
method of exhaustion

図形の面積や体積を求める一つの方法であって，定積分の基礎となる考え方である。たとえば，y＝x²＋1 ，あるいは y＝ sin x＋1 のような関数 y＝f(x) が与えられたとき，x 軸と曲線 y＝f(x) および2直線 x＝a，x＝b(a＜b) で囲まれた領域の面積 S を求める場合を考えると，この領域は，その境の一部になめらかな曲線を含むから，一般に，長方形や三角形に余すところなく分割することはできない。それで，区間 [a，b] をいくつかの小部分に区分し，そのすべての区分点から垂線を立てて，領域を細い柱状の図形に細分する。ここで各柱の上側の曲線部分における最高の高さと最低の高さの中間の値を柱の高さとするような長方形をつくり，初めに細分された柱状の図形と置き換える。こうしてできたすべての長方形の面積の和 S' は，面積 S の近似値を与える。そして区間を細かく区分すればするほど，長方形の数が多くなり，近似の精度が高まる。このようにして，分割を限りなく細かくしたときの，あらゆる長方形の面積の和の極限値として S を計算する方法を区分求積法という。

出典　ブリタニカ国際大百科事典 小項目事典