垂直（読み）スイチョク

デジタル大辞泉

すい‐ちょく【垂直】

［名・形動］
１ まっすぐに垂れ下がること。また、そのさま。「垂直な線を引く」
２ 水平面・地平面に対して直角の方向を示すこと。また、そのさま。「がけが垂直に切り立つ」
３ 数学で、直線と直線、直線と平面、平面と平面とが直角に交わること。
[類語]鉛直・直角

出典　小学館

精選版 日本国語大辞典

すい‐ちょく【垂直】

1. 〘 名詞 〙 ( 形動 )
2. ① まっすぐに垂れていること。また、そのさま。
3. ② 水平面・地平面に対して直角の方向を示すこと。また、そのさま。物体を糸でつった時、糸が示す線の方向。重力の方向。鉛直。〔物理学術語和英仏独対訳字書（1888）〕
   1. [初出の実例]「お種さんは大きな麦藁帽の縁が垂直になる程俯向いてゐる」(出典：灰燼（1911‐12）〈森鴎外〉一三)
4. ③ 数学では、( 1 )二つの直線が互いに九〇度で交わること、( 2 )一つの直線が一つの平面と交わり、その平面に含まれその交点を通るすべての直線と九〇度で交わること、( 3 )二つの平面が交わり、一方が他方と九〇度で交わる直線を含むこと、をいう。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

垂直
すいちょく

同一平面上の2直線が交わってできる角が直角であるとき、2直線は垂直であるという。点Aを通って直線lに垂直な直線がlと交わる点をHとするとき、線分AHをAからlへ下ろした垂線といい、Hを垂線の足、線分AHの長さを垂線の長さという。このAHは、Aからlに至る線のなかで長さのもっとも短いものである。

　空間での垂直を次のように定義する。

〔1〕2直線の垂直　2直線l、l′に対し、点Oを通ってそれぞれに平行に引いた2直線が垂直であるとき、lとl′は垂直であるといい、l⊥l′と書く。点Aとこれを通らない直線lがあるとき、Aを通ってlに垂直に交わる直線を引き、その交点をHとするとき、AHをAからlに下ろした垂線という。

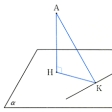
〔2〕直線と平面の垂直　直線hが平面α上のすべての直線に垂直のとき、hはαに垂直であるといい、h⊥αと書く。直線hが、平面α上にあって平行でない2直線に垂直のとき、hはαに垂直である。平面α上にない点Aを通ってαに垂直な直線がαと交わる点をHとするとき、線分AHをAからαへ下ろした垂線といい、Hを垂線の足という。垂線AHは、Aからα上の点に至る線のなかで、長さのもっとも短いものである。

〔3〕2平面の垂直　2平面α、βのつくる角が直角のとき、αとβは垂直であるといい、α⊥βと書く。これは、α、βの交線上の点を通って、各平面上で交線に引いた垂線が垂直になっている場合である。直線hが平面αに垂直のとき、hを含む平面はαに垂直である。

［栗田　稔］

三垂線の定理

平面α上にない点A、α上の直線l、l上の点K、α上の点Hについて次の定理が成り立つ。これらが三垂線の定理である（(1)だけを三垂線の定理、(2)(3)をその逆ということもある）。

　(1)直線AH⊥α, HK⊥lならばAK⊥l
　(2)直線AH⊥α, AK⊥lならばHK⊥l
　(3)AH⊥HK, HK⊥l, AK⊥lならばAH⊥α
［栗田　稔］

座標と垂直

(1)平面上で直角座標を考えるとき、直角成分が（a₁, a₂), (b₁, b₂）である二つのベクトルが垂直であるための条件はa₁b₁＋a₂b₂＝0である。また、2直線
　　y＝m₁x＋k₁, y＝m₂x＋k₂
が垂直であるための条件はm₁m₂＝－1である。

(2)空間で直角座標を考えるとき、直角成分が(a₁, a₂, a₃), (b₁, b₂, b₃)の二つのベクトルが垂直であるための条件は
　　a₁b₁＋a₂b₂＋a₃b₃＝0
である。また、平面
　　ax＋by＋cz＋d＝0
については、（a, b, c）はこの平面に垂直なベクトルの直角成分で、2平面
　　ax＋by＋cz＋d＝0, a′x＋b′y＋c′z＋d′＝0
が垂直になるための条件は
　　aa′＋bb′＋cc′＝0
である。

［栗田　稔］

三垂線の定理

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

垂直 (すいちょく)
perpendicular

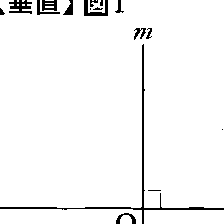
l，mを空間内の異なる2直線とする。lとmが交われば，これら2直線は一平面上にあって，交点Qを頂点とする四つの角ができ，その一つが直角ならば他の角もすべて直角となる。このときlとmは垂直である，または直交するという（図1）。lとmが交わらない場合も，1点を通ってそれらに平行にひいた2直線が直交するならば，lとmは垂直であるという（図2）。lとmが垂直であることをl⊥mで表す。一直線lと一平面αが1点で交わり，交点Qを通るα上の二つの直線がlと直交すれば，α上のすべての直線はlと垂直となる。このときlとαは垂直である，または直交するといい，l⊥αと表す（図3）。異なる2平面α，βが交わっていて，その交線lにおいてつくる2面角が直角のとき，すなわち，lに垂直な平面とα，βとの交線m，nが垂直のとき，αとβは垂直である，または直交するといい，α⊥βで表す（図4）。
執筆者：中岡 稔

図1～図4

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

垂直
すいちょく
perpendicularity

(1) 2直線 l，g が交わってつくる角が直角であるとき，一方は他方に垂直，あるいはこの2直線は互いに垂直であるといい，l⊥g と書く。このとき l と g とは互いに他の垂線であるといい，その交点を垂線の足と呼ぶ。 (2) 直線 l が平面 α 上の1点を通り，またその点を通る α 上のすべての直線と垂直なとき，l と α は互いに垂直であるといい，このような直線 l を平面 α の垂線という。これを l⊥α で表わす。2直線 a，b の定める平面を α とするとき，a⊥l ，b⊥l ならば，l⊥α である。 (3) 2平面 α，β が直線 l で交わり，l 上の1点Pにおいて，α 上に l と垂直な直線 a を，β上に l と垂直な直線 b を引いたとき，a⊥b ならば，αとβは互いに垂直であるといい，α⊥β と書く。3平面α，β，γについて，α⊥β ，α⊥γ のとき，β，γが交わり，その交線を l とすれば，l⊥α である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

垂直【すいちょく】

以下の場合，二つは互いに垂直であるという。（１）二直線。両者が互いに交わり，その交角が直角のとき（一般には，一点を通り二直線に平行に引いた直線が直角をなすとき）。（２）直線と平面。直線が平面上のすべての直線と直交（直角に交わること）するとき（実際は平面上の異なる二直線と直交すれば，平面上のすべての直線と垂直）。（３）平面と平面。二平面の交線上の一点を通り，各平面上に交線に直角に引いた二直線が直交するとき。
→関連項目垂線

出典　株式会社平凡社

普及版 字通

【垂直】すいちよく

直下。

字通「垂」の項目を見る。

出典　平凡社「普及版 字通」