日本大百科全書(ニッポニカ) 「実体振り子」の意味・わかりやすい解説
実体振り子
じったいふりこ
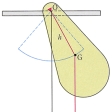
剛体に軸を貫き通し、この軸を水平な軸受で支えて振り子としたもの、または剛体に懸垂用のナイフ・エッジを取り付け、ナイフ・エッジの先端を水平な台の上に据えて振り子にしたものをいう。実体振子(しんし)、物理振り子、複振り子あるいは剛体振子とよぶ。剛体の回転軸の周りの慣性モーメントをI、質量をM、重心から回転軸までの距離OGをhとすると、実体振り子の振動の周期Tは、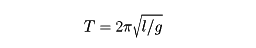
となる。ここにlはl=I/(Mh)で、gは重力の加速度である。実体振り子の周期Tは、糸の長さlの単振り子の周期と同じ値をもつ。lは相当単振り子の長さとよばれる。
重心を貫き実体振り子の回転軸に平行な軸の周りの慣性モーメントをI0=Mk02とする(k0は回転半径とよばれる)と、回転軸の周りの慣性モーメントIは、
I=I0+Mh2=M(k02+h2)
相当単振り子の長さlの値は、
l=h+(k02/h)[=gT2/(4π2)]
となる。重心と回転軸との距離hは、二次方程式h2-lh+k02=0を満足する。したがって、同一の周期Tを与えるhには、この方程式の二つの根h1とh2とがある。
二次方程式における根と係数との関係h1+h2=lと前述のlとTの間の関係を用いて、重力の加速度gを測定する装置にケーターKaterの可逆振子がある。
[飼沼芳郎]


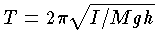 となる。
となる。