振り子（読み）ふりこ（英語表記）pendulum

日本大百科全書(ニッポニカ)

振り子
ふりこ
pendulum

一定の周期で、一定の軸または点の周りを運動する物体をいう。振子(しんし)ともいう。軽い糸の先端におもりをつけて振れば振り子になる。糸でなくても、剛体（力を加えても、たやすくは形質の変わらない物体）を1点で固定して、自由に回転できるようにしたときも、振り子ができる。これを実体振り子（剛体振り子または複振り子）という。紐(ひも)の振り子、または実体振り子が鉛直面内で微小振動するとき（これを単振り子という、図A）、その周期は、それぞれ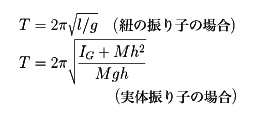

となる。ここにlは紐の長さ、gは重力加速度、I_Gは剛体の重心を通り回転軸に平行な軸の周りの回転軸に関する慣性モーメント、Mは剛体の質量、hは回転軸と重心の距離である。これらの周期は、微小振動である限り、その振幅には無関係である。このことを振り子の等時性という。実体振り子の等時性は、振り子時計に応用されている。

［大槻義彦］

振り子の種類

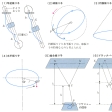
実体振り子の場合、周期Tは、hに関して二価関数である。すなわち、同じ周期を与える異なるhの値が存在する。それらをh₁、h₂とすると、hがh₁のところを固定しても、hがh₂のところを固定しても、この振り子の周期は同じである。これを可逆振り子という（図Bの(1)）。

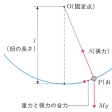
　紐におもりをつけた振り子の場合、かならずしも鉛直面内だけで運動をするとは限らない。おもりは重力の作用のもとで、紐の長さの半径の球面上に束縛された運動をする。これを球振り子とよぶ（図Bの(2)）。球振り子の特殊なものに円錐(えんすい)振り子と水平振り子がある。円錐振り子は図Bの(3)のように、紐は鉛直線とある一定の角度θをなして円運動をする。この場合、おもりの質量をMとし、円運動の角速度をωとすると、遠心力は
　　Mlsinθω²
であり、これが重力と紐の張力とつり合う。すなわち、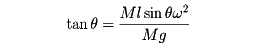

つまり、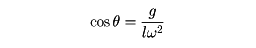

なる式によって、θが決定される。角度θが90度の場合、おもりは水平面内の円運動となり、水平振り子とよばれる（図Bの(4)）。これは、重力加速度gが無視できる近似の場合である。

　振り子を図Bの(5)のように連結したものを結合振り子という。結合振り子が同じ鉛直面内で運動するときでも、問題を解くのは複雑である。これは連制振動の問題とよばれている。紐の支点を複雑にして、おもりが特別な運動をするようにしたものに「ブラックバーンのY形振り子」がある。これは、紐を二つの支点でY字形に固定したものである（図Bの(6)）。こうすることによって、図のx方向とy方向の（単振り子の）振動数と位相が異なるようにする。位相の違いと振動数の違いに応じて、おもりは、いわゆるリサジューの図形を描く。

［大槻義彦］

弾性振動による振り子

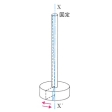
これまで述べてきた振り子とは物理的にはだいぶ違うが、振り子とよばれる特別な振動がある。ばね振り子とかねじれ振り子とかよばれるものがそれである。ねじれ振り子は、剛体の細い棒、ないし針金のねじれの振動である（図C）。下部につるされた物体の慣性モーメントをIと置くと、ねじれの単振動の周期は2π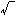（I/c）である。ここにcは、ねじれ剛性率nを針金の長さで割ったものである。

［大槻義彦］

[参照項目] | 円運動 | 実体振り子 | 振動 | リサジューの図形

単振り子に働く力〔図A〕

振り子の種類〔図B〕

弾性振動による振り子（ねじれ振り子）〔…

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

振り子
ふりこ
pendulum

固定点または固定軸からつるされ，重力の作用のもとで，これらのまわりに周期運動する物体。普通は振動する場合をさすが，広義には旋回運動する場合も含める。一端を固定した軽い糸または棒の他端に質点をつるしたものを質点振り子，固定軸からつるされてこの軸のまわりに振れる物体を実体振り子という。ねじり振り子は吊り糸のねじれ弾性によってねじれ振動する弾性振り子であって，重力の作用で振動する前述のような振り子とは異なる。

出典　ブリタニカ国際大百科事典 小項目事典