弾性係数（読み）だんせいけいすう（英語表記）elastic coefficient

精選版 日本国語大辞典

だんせい‐けいすう【弾性係数】

〘名〙 ＝だんせいりつ（弾性率）〔電気工学ポケットブック（1928）〕

出典　精選版 日本国語大辞典

デジタル大辞泉

だんせい‐けいすう【弾性係数】

⇒弾性率

出典　小学館

改訂新版　世界大百科事典

弾性係数 (だんせいけいすう)
elastic coefficient

固体のひずみと応力は，ひずみが小さいときはほぼ比例関係にある（フックの法則）。この比例係数を弾性係数，または弾性率modulus of elasticityという。応力の成分，ひずみの成分はそれぞれ6個あるので，弾性係数の数は36個あることになるが，応力，ひずみは対称テンソルであるから，独立な係数の数はもっとも一般的な場合21個である。結晶の対称性が増すと独立な係数の数が減り，対称性のもっとも大きい立方晶系では3個となり，さらに等方的な物質では2個になる。このほかに，結晶を構成する原子どうしの相互作用ポテンシャルが中心力（ポテンシャルが相互の距離のみに依存する）の場合，コーシーの関係と呼ばれる関係がある。

　もっともふつうに使われる弾性係数は，ヤング率，剛性率（ずれ弾性率），体積弾性率，ポアソン比である。これらは等方弾性体について次のように定義される。（1）ヤング率　一つの方向に引張応力（または圧縮応力）σが働くとき，その方向の伸びのひずみεとの比E＝σ/εをいう。（2）剛性率　せん断応力τとずれのひずみγとの比G＝τ/γをいう。（3）体積弾性率　弾性体に一様な圧力pが加わるときの体積ひずみ⊿V/Vとの比として，K＝－p/（⊿V/V）で表される。これら三つの弾性係数は，ふつうの金属などではほぼ10¹⁰N/m²程度の大きさをもつ。（4）ポアソン比　一つの方向に引張応力を作用させると，その方向に伸びのひずみεを生ずるとともに，それに垂直な方向にも縮みのひずみε′を生ずる。このときν＝｜ε′/ε｜をポアソン比と呼ぶ。νは0と0.5の間の値になり，ν＝0.5は体積の変化を生じない場合であり，弾力ゴムでは0.46～0.49である。ふつうの物質ではνは0.3の近傍の値になっている場合が多い。

　等方性弾性体ではヤング率，剛性率，体積弾性率，ポアソン比は独立ではなく，相互に関係づけられる。前述のように，等方性弾性体で独立な弾性係数は2個であり，その2個としてよく用いられるものに，フランスのラメGabriel Lamé（1795-1870）によって導入されたラメの弾性係数（ラメの定数ともいう）λ，μがあるが，これを用いると，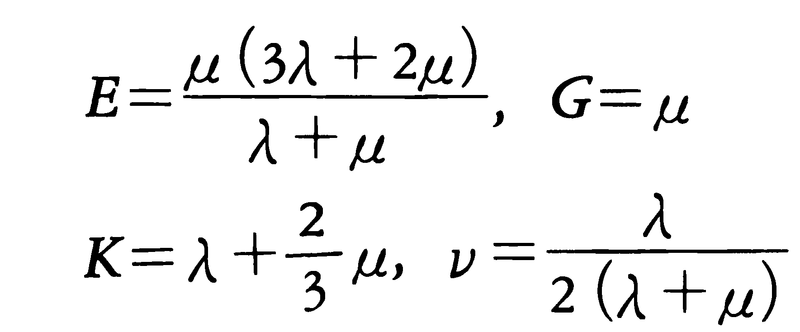

の関係がある。
執筆者：二宮 敏行

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

弾性係数
だんせいけいすう
elastic modulus; modulus of elasticity

弾性体の比例限度内では応力とひずみは比例し，その間の比例定数は物質特有の値をとる（温度によって変わる）。この値を物理学では弾性率，弾性定数などと呼び，工学では弾性係数という。一般の弾性体では 36個の比例定数が存在するが，等方・等質の場合には 2個となり，ラメの定数と呼ばれる λ，μがその例になる。しかし，λは物理的意味をもたないので，工学ではもっぱら次の弾性係数を用いる。(1) 縦弾性係数またはヤング率 E　伸び弾性率ともいい，棒材を引っ張るときのように，単軸の垂直応力 σと縦ひずみ εの比例関係 σ＝Eεを表す定数。(2) 横弾性係数，剛性率または剪断弾性係数 G　丸棒をねじるときのように，剪断応力 τと剪断ひずみ γの比例関係 τ＝Gγを表す定数。(3) 体積弾性係数 K　水中に置かれた直方体の体積変化のように，各側面に作用する垂直応力の平均値 σ_m と，体積ひずみ ε_v（単位体積あたりの体積変化。体積膨張率ともいう）の比例関係 σ_m＝Kε_v を表す定数。ここで，σ_m は平均応力または静水圧応力とも呼ばれ，各垂直応力を σ₁，σ₂，σ₃とすれば，σ_m＝（σ₁＋σ₂＋σ₃）/3で与えられる。(4) ポアソン比 ν　丸棒を伸長すれば，軸方向に伸びるとともに直径は細くなる。いま，軸方向のひずみを縦ひずみ ε，直径方向のひずみを横ひずみ －ε'とし，その比に負号をつけた値すなわち ν＝－ε'/εをポアソン比，その逆数 1/νをポアソン数という。νの値は 0.5より大きくはならない。これらの係数の間には関係式 E＝2G（1＋ν）＝3K（1－2ν）があるから，いずれか二つの測定値がわかれば，ほかは計算によって求められる。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

弾性係数【coefficient of elasticity】

通常は「弾性率」という．ヤング率＊，体積弾性係数，剪断弾性係数の総称である．応力の増分と歪みの増分の比である．

出典　朝倉書店

栄養・生化学辞典

弾性係数

　→剛性率

出典　朝倉書店