最適制御（読み）さいてきせいぎょ（その他表記）optimal control

改訂新版　世界大百科事典

最適制御 (さいてきせいぎょ)
optimal control

動的な過程を最適化するための一般的な制御方法をいう。線形計画法や非線形計画法と対比されるが，静的な最適化にくらべ動的な最適化ははるかに複雑な問題で，かなり高度の理論とめんどうな計算を必要とする。最適制御の理論的基礎は，ソ連の数学者L.S.ポントリャーギンによって導かれた最大原理とアメリカの数学者ベルマンRichard Bellmanによって提案された動的計画法にある。両者は1960年前後にほぼ同時に確立された。

　制御対象を動的なプロセスとして数学的に表現し，ある動作指標performance indexを決めれば，最適制御理論を用いてその動作指標の下での最適な特性をもつ制御系を構成することができる。これは制御対象のダイナミクスの時間領域における表現を直接用いて，制御系の時間的な振舞いを厳密に最適化する方法であり，周波数領域におけるダイナミクスの表現にもとづき幾つかの設計仕様と制約条件の間の妥協をはかる伝統的な制御系設計法の対極に立つ考え方である。

　動作指標は最適制御を用いた制御系の特性を決定づける重要な因子である。たとえば直線上を大きさの上限（便宜上1とする）をもつ推力u（t）をうけて運動する単位質量の質点を考えよう。ニュートンの運動法則より質点の運動方程式は

　d²x（t）/dt²＝u（t）　（｜u（t）｜≦1）

となる。初期条件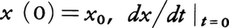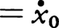が与えられたとき，質点を最短時間で原点に移しそこで静止させる推進力u^＊（t）をもとめるには，評価関数J（u）と終端条件を

とおけばよい。J（u）を最小にすることが，質点が原点に到達し静止するに要する時間Tを最小にすることである。最適制御理論を用いると上の最適化問題の解，すなわち最適入力u^＊（t）は次のようにもとめられる。いまx₁＝x，x₂＝dx/dtとおき，位相面，すなわち（x₁，x₂）平面で最適制御u^＊（t）に対応する運動方程式の解軌道trajectoryを描くと図のようになる。この図で曲線OAは放物線x₁＝1/2x₂²の下半分であり，曲線OBはOAに原点対称な曲線である。質点の運動状態が曲線BOAの下にあるときはu^＊（t）＝＋1で，上にあるときはu^＊（t）＝－1が最適制御である。｜u^＊（t）｜≦1なる制約条件が課せられていることに注意されたい。したがってたとえば点Pを初期状態とすると，最適制御はまずu＝－1となり，対応する軌道は破線PQとなる。軌道がOAと交わる点Qに到達すると最適制御はu＝＋1に切りかわり，対応する軌道はOAに沿って進み原点に到達する。これが最短時間で原点に到達する質点の運動軌跡である。初期状態P′から出発した場合も同様である。曲線BOAは，その上に軌道が到達したとき最適入力が－1から＋1または＋1から－1に切りかわるので，切りかえ曲線switching curveと呼ばれる。この例のように最適制御の振幅がつねに許される最大値（＋1または－1）をとり，その符号だけが切りかわる制御をバン・バンbang-bang制御と呼ぶ。

　上の例は最短時間制御と呼ばれる最適制御の一つのクラスに属するが，動作指標のとり方により種々の最適制御問題が考えられる。たとえばある初期状態から他の状態へ最小の入力パワーで到達させるための最小燃料制御や，出力の原点からの2乗偏差面積と入力パワーの大きさとの重みつき荷重和を動作指標とする最適レギュレーターなどがある。また制御対象のダイナミクスも微分方程式であらわされる集中定数連続時間システムだけでなく，差分方程式であらわされる離散時間システムや偏微分方程式であらわされる分布定数システム，統計的な外乱を含む確率的なシステムなどに対しても最適制御理論は確立されている。

　最適制御は決められた基準の下で理論的に厳密な最適化が達成されるということから，高度の性能を要求される制御系の構成に有力な方法を与える。したがって航空機の運動制御，高速精密なマニピュレーターの運動制御，クレーンの振れ止め制御などに着実に応用が進んでおり，社会経済システムの最適政策決定など工学以外の分野にも応用が広がりつつある。しかし具体的に最適制御入力をもとめるにはかなりめんどうな数値計算を実行する必要があり，そのアルゴリズムは一部の場合を除き完全に確立されたとはいいがたいのが現状である。また数値計算の結果，最適解は時間関数の形で得られるのが普通であり，実際の制御系の設計として重要なフィードバック制御の形に変換するのが困難な場合が多い。このような数値計算上の困難は制御対象の次数が大きくなるにつれて倍加し，最適制御のスムーズな応用を阻む要因となっている。しかし線形の制御対象に対する最適レギュレーターは数値計算が簡単なうえに，つねに線形の状態フィードバックによって実現されるので，実際の制御系への応用はかなり進んでいる。最適レギュレーターによって設計された制御系は安定性が非常によく，パラメーター変動にも強いことが理論的にも確かめられており，伝統的な設計法よりもすぐれた性能を示す。最適レギュレーターは一つの制御技術として成熟しつつあり，最適制御理論が応用面において生み出した大きな成果である。
執筆者：木村 英紀

図－最適制御

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

最適制御
さいてきせいぎょ

→制御理論

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の最適制御の言及

【確率制御】より

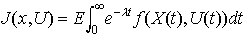…評価関数，を最大(あるいは最小)にするように許容されるコントロールを選ぶのが確率制御である。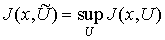(価関数という)となる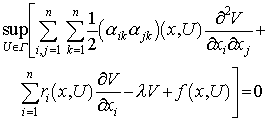を最適制御と呼ぶ。価関数は適当な条件の下でベルマン方程式，を満たし，左辺の最大値を与える(x)により最適制御を求めることができる。…

【最大原理】より

…自動制御系の設計法の一つに最適制御があるが，最大原理は最適制御の基礎となる定理で，1950年代の終りにソ連の数学者ポントリャーギンらによって確立された。この原理は制御系の設計法に新しい視点を導入し，60年代の現代制御理論の発展の原動力となった。…

※「最適制御」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」