粒度分布（読み）りゅうどぶんぷ（英語表記）size distribution

改訂新版　世界大百科事典

粒度分布 (りゅうどぶんぷ)
size distribution

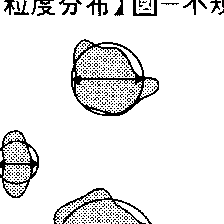
粉粒体を構成する粒子群の粒子径の分布。粉粒体は一般に不規則な形状をもち，大きさのふぞろいな粒子より構成されている。不規則形状の粒子の粒子径particle sizeを表すには，3軸平均径，円相当径（ヘイウッドHeywood径），定方向径（フェレーFeret径），面積等分径（マーチンMartin径），ストークスStokes径などが用いられる。3軸平均径は粒子の長さ，幅，厚さの算術平均である。円相当径は粒子の投影面積と等しい面積をもつ円の直径である（図のa）。定方向径は一定方向の接線間距離によって定義される（図のb）。面積等分径は粒子の投影面積を2分する一定方向の線の切片長である（図のc）。このように，ストークス径は粘性流動条件下において粒子と密度が等しく，同じ沈降速度をもつ球形粒子の直径として定義される。

　粒度分布を有する粒子群の粒度を平均値などの指標によって表すには，後に述べる種々の粒度分布関数による方法と，粒度分布関数によらない方法とがある。後者としては個数，長さ，面積，体積あるいは質量を基準とする長さ（粒子径）の平均，面積の平均，体積または質量の平均など種々の平均値のほか，分布の最頻値に対応する粒子径（モード径という），分布の中央値に対応する粒子径（メジアン径という）などがある。また粒度分布を概数的に表示するには，〈－74μm23%〉というような表現がしばしば用いられる。これは74μm以下の粒子が粒子群の全質量の23%存在する，という意味である。任意の基準粒度よりも小さい粒子の質量（または質量割合）を通過分，それよりも大きい粒子の質量（または質量割合）を残分（ざんぶん）と呼ぶ。通過分，残分はそれぞれふるい下，ふるい上あるいは網下，網上などと俗称される場合もある。通過分80%に対応する粒度は80%通過粒度あるいは単に80%粒度と呼ばれる。

粒度分布関数size distribution function

粒度分布のあてはめに使われる関数であり，以下に示す3種の関数が最も広く知られている。

（1）ゲーツ=ゴーダン=シューマンGates-Gaudin-Schuhmann分布は次式によって示される。

ここにD_pは粒度，Pは通過分を表す。（1）式は二つのパラメーターKおよびαによって決まる。Kは粒度指数と呼ばれ，通過分P＝1（100%）に対応する粒度を表す。αは分布指数と呼ばれ，分布の広がりの大小を特性づける。Kが大きいほど粒子は粗く，αが大きいほど分布の広がりは狭い。（1）式はD_pとPの対数をそれぞれ横軸および縦軸とするグラフによって示される。

（2）ロジン=ラムラーRosin-Rammler分布は次式によって示される。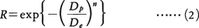

ここにRは残分を表し，二つのパラメーターD_eおよびnはそれぞれ粒度特性値，粒度分布指数と呼ばれている。（2）式を直線で表示し，二つのパラメーターを評価するためにはふつう，横軸に対数，縦軸に2重対数をとった特殊な線図が用いられる。これをロジン=ラムラー分布線図という。D_eはR＝1/e≒0.368に対応する横座標値より求められ，nはグラフと平行に極Pから引いた直線と右上の補助目盛線との交点より求められる。ロジン=ラムラー分布は粉砕産物などに比較的よく適合する場合が多く，広く用いられている。

（3）対数正規分布は粒子径の対数に対する粒子径の分布密度として正規分布をあてはめたものである。すなわち粒子径D_pに対する分布密度fは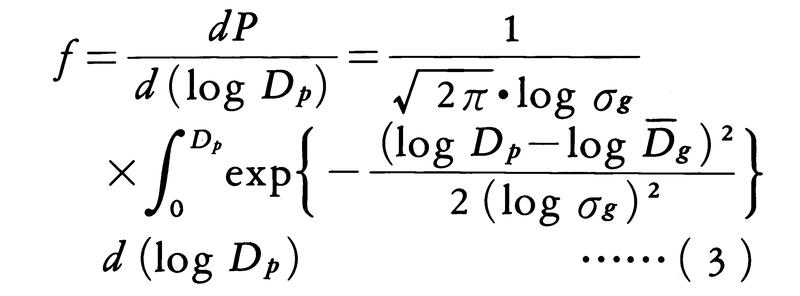

によって与えられる。ここに二つの特性パラメーターD_gおよびσ_gはそれぞれ幾何平均径および幾何標準偏差である。対数正規分布へのあてはめを試みるには対数正規確率紙を利用するのが簡便である。D_gは通過分50%に対応する粒度として，またσ_gは正規分布の性質より通過分約16%，50%，84%に対応する粒度の比として求められる。対数正規分布は個数分布と質量分布の換算や各種平均径間の換算が容易であるという特徴があり，ふるい分けにより整粒したものなど，粒度のよくそろった粉粒体の粒度分布に対しては概して適合性がよい。
執筆者：井上 外志雄

図－不規則な形状の粒子の粒子径の定義例

出典　株式会社平凡社「改訂新版　世界大百科事典」

化学辞典 第2版

粒度分布
リュウドブンプ
particle size distribution

ある粒子径範囲に属する粒子の全体量に対する割合．粉体の粒度分布の表示法としては次の三通りがある．
(1)頻度分布：ある粒径範囲に属する粒子量の全粒子量に対する割合，
(2)積算分布(ふるい下)：ある粒径以下の粒子量の全粒子量に対する割合，
(3)積算分布(ふるい上)：ある粒径以上の粒子量の全粒子量に対する割合．
粒子量としては，体積，面積，長さ，個数が用いられる．粒度分布は古くはふるい分けにより求められてきたが，現在では，次にあげるようなさまざまな測定法がある．
(1)液相沈降法(遠心沈降光透過法，X線透過法，遠心沈降重量法)：流体中を沈降する粒子の速度を光透過，X線透過，重量変化により観測し，それから粒度分布を算出する方法，
(2)レーザー回折散乱法：液体あるいは気体に分散された粒子にレーザー光を照射し，回折あるいは散乱される光の強度を，フラウンホーファー回折理論やミー散乱理論にもとづき解析し，粒度分布を算出する方法，
(3)遮光法：粒子にさえぎられたレーザー光の光量を検知して，粒度分布を算出する方法，
(4)電気的検知法：電解質溶液などの電気伝導性のある液体中に粒子を懸濁させ，その粒子の体積と個数を電気的に検知する方法，
(5)光相関法：粒子により散乱される光の散乱強度の経時変化から粒子の拡散係数を算出し，粒子の大きさを解析する方法，
(6)クロマトグラフィー：液体の流れに試料を投入し，層流に存在する速度分布を利用して粒子を大きさ別に取り出し，その濃度を光透過法などで測定する方法，
(7)画像解析法：顕微鏡画像を解析し，粒度分布を算出する方法．

出典　森北出版「化学辞典（第2版）」

岩石学辞典

粒度分布

→粒径頻度分布

出典　朝倉書店

栄養・生化学辞典

粒度分布

　粒子の粒度がどのように分布するかを示すもの．

出典　朝倉書店