主成分分析（読み）シュセイブンブンセキ（英語表記）principal component analysis

デジタル大辞泉

しゅせいぶん‐ぶんせき【主成分分析】

多変量解析において、分析対象を特徴づける複数の変数の中から、より対象の特徴を総合的に説明できる少数の変数、すなわち主成分を選択する統計的技法。PCA（principal component analysis）。

出典　小学館

最新 心理学事典

しゅせいぶんぶんせき
主成分分析
principal component analysis

PCAと略称される。多数（ｐ個）の変数の変動をより少数（ｍ≦ｐ個）の成分に縮約するための多変量解析法である。個体ｉに対する変数ｊのデータｘ^ijからなるｎ個体×ｐ変数のデータ行列ＸにPCAを適用すると，個体ｉの第ｒ主成分得点principal component score f^ir（ｒ＝1，…，ｍ），さらに変数ｊの第ｒ主成分への負荷量loading a^jrが得られる。たとえば5変数の散布図は，3次元の世界に住むわれわれには描けないが，第1，第2主成分得点ｆⁱ¹，ｆⁱ²を座標値とした散布図で5変数の主要変動を可視化でき，変数と主成分の関係はａ^jrから解釈できる。以下，データｘ^ijは，個体ｉを通した平均が0の平均偏差得点とする。PCAの定式化は2種に大別される。

　その一つはホテリングHotelling,H.（1933）により，分散最大maximum varianceの変数の重みつき合計weighted sum of variablesを求めることとして，PCAは定式化される。すなわち，ｗ^jrで重みづけられた変数ｘ^ijの合計



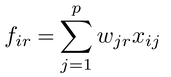
を個体ｉの第ｒ主成分得点とする。ただし，第1主成分得点の重みｗ^j1は，条件



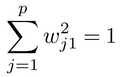
のもとで，個体を通した



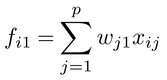
の分散を最大にするｗ^j1である。したがって，ｆⁱ¹は個体差を最大にする得点となる。さらに，第2以降の主成分得点の重みｗ^jr（ｒ≧2）は，得点がそれより上位の主成分得点と無相関になり，かつ



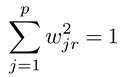
という条件のもとで，個体を通したｆ^irの分散を最大にするｗ^jrである。

　もう一つの定式化はピアソンPearson,C.（1901）に由来し，PCAを主成分得点の重みつき合計weighted sum of principal component scoresによるデータ近似data approximationとみなすものである。すなわち，負荷量ａ^jrで重みつけられた得点ｆ^irの合計



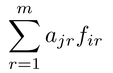
とデータｘ^ijとの残差平方和



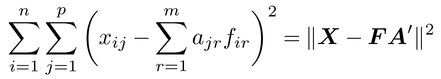
を最小にする



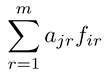
を求めることとして，PCAは定式化される。ここで，Ｆはｆ^irからなるｎ個体×ｍ成分の主成分得点行列，Ａはａ^jrからなるｐ変数×ｍ成分の負荷行列である。Ａ′Ａを単位行列とする制約条件下では，ｆ^irの解は前段の



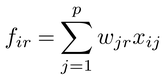
と一致する。また，ｘ^ijが標準得点のとき，ｎ^-1Ｆ′Ｆを単位行列とする制約条件下では，負荷量ａ^jrの解は，変数ｊと第ｒ主成分得点の相関係数と一致する。

　後者の定式化で重要になるのは，いかなる行列も三つの行列の積KΛL′に分解されることであり，これを特異値分解singular value decomposition（SVD）とよぶ。ここで，Ｋ′ＫとＬ′Ｌは単位行列，Λは対角要素が降順の対角行列である。データ行列ＸのSVDをX＝KΛL′と表わすと，残差平方和∥Ｘ－FA′∥²を最小にするFA′がＫ^mΛ^mＬ′^mとなることを，エッカートEckart,C.とヤングYoung,G.（1936）が証明している。ここで，Λ^mはΛの左上の要素からなるｍ×ｍの対角行列，Ｋ^mとＬ^mはそれぞれＫとＬの上位ｍ列からなる。なお，Ｘ＝KΛL′よりｎ^-1Ｘ′Ｘ＝Ｌ（ｎ^-1Λ²）Ｌ′であり，ｎ^-1Λ²の対角要素が共分散行列の固有値eigenvalueとなる。

　PCAの拡張手法に，タッカーTucker,L.R.（1966）が草案し，1980年以降にオランダの計量心理学者を中心に確立された三相主成分分析three-way principal component analysisがある。これは三相配列のデータから，各相に対応する成分を求めるPCAである。三相配列の例として，複数受験者が複数条件で複数のテストを受けて得られる受験者×条件×テストの得点が挙げられ，この条件では受験者・条件・テストが相となる。　→因子分析　→多変量解析
〔足立 浩平〕

出典　最新 心理学事典

改訂新版　世界大百科事典

主成分分析 (しゅせいぶんぶんせき)
principal component analysis

統計的多変量解析法の基本的手法。ある集団についてその個体の特徴が多くの変数で測定されているとき，個体の特徴を総合的に表現する少数の指標を求めることを目的とする。例えば，各企業の活動結果や財務状況は売上高，利益，資本金，負債額など多くのデータで示されるが，企業の評価のための少数の指標（主成分または成分といわれる）が主成分分析によって構成される。

　変数を仮に3個としてx，y，wと書くと，主成分はz＝ax＋by＋cwというように変数の一次結合（重みつきの和）として表現され，個体ごとの（x，y，w）の値を代入して主成分値が求められる。普通は，各変数は平均0，標準偏差1に標準化され，一次結合の重みはその変数と主成分との相関係数（例えば，aはxとzの相関係数）になっている。一般にp変数n個体のn×pのデータとすると，pは数十から100，nは数百から数千ということも珍しくない。主成分は3～7個ぐらいが互いに無相関になるようにとられ，データ全体の変動を代表し要約するように構成される。

　第1主成分は，もとの変数の変動をできるだけ反映するように，例えば，xの値が大きい個体に対しては主成分値zも大きくなるようにしたいという考えを相関係数で表現し，各変数と主成分との相関係数の2乗の和，3変数の場合ならばr²（z，x）＋r²（z，y）＋r²（z，w）を最大にするものと定式化される。この式で，r（z，◦）は主成分とある変数との相関係数を表し，相関係数の正負は絶対値が同じならzが変数を代表する程度に関係しないと考えて2乗している。第2主成分以下は第1主成分と無相関という条件で（幾何学的にいえば直交方向に），同じように各変数の変動を代表するように構成される。実際の計算では，もとの変数の間の相関係数を並べた相関係数行列の固有ベクトルが主成分の方向を定め，固有値が主成分と各変数の相関係数の2乗の和を表すということを用いる。

　求められた主成分は，因子分析のときのようにその現実的意味が解釈されて，個体の類型化や特徴の記述に用いられる。企業財務の分析では，企業の安定性や成長性などの成分が抽出され，レーダーチャートなどで図式化されて利用されている。
執筆者：吉沢 正

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブランド用語集

主成分分析

主成分分析とは複数の変数を合成して元の変数を減らし、全体を少数の変数で説明できるようにする多変量解析の手法のことをいう。

出典　(株)トライベック・ブランド戦略研究所

世界大百科事典（旧版）内の主成分分析の言及

【パターン認識】より

…たとえば，人の顔の認識のための目や鼻など，機械部品では角や穴など，あるいは屋内自動走行車のためには廊下の境界やドアなどの境界線である。どの特徴をどのようにして抽出したらよいかを決める一般的理論はないが，いくつかの特徴の候補が与えられたとき，どの特徴が有効であるかを統計的に評価する方法はある(主成分分析あるいは固有ベクトル法など)。有効な特徴から順に選択していき，いくつかの入力パターンに対して認識実験を行って，適当な数の特徴を決めることができる。…

※「主成分分析」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」