錯視（読み）サクシ（英語表記）optic illusion

デジタル大辞泉

さく‐し【錯視】

視覚における錯覚。形・大きさ・長さ・色・方向などが、ある条件や要因のために実際とは違ったものとして知覚されること。

出典　小学館

精選版 日本国語大辞典

さく‐し【錯視】

1. 〘 名詞 〙 ( [英語] optical illusion の訳語 ) 長さ、形、大きさ、方向、色、奥行などの視覚の領域で生じる歪みのこと。幾何学的錯視、遠近の錯視など多くの例がある。〔医語類聚（1872）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

錯視 (さくし)
optic illusion

視覚領域における錯覚をいい，他の感覚領域のものと同じようにいくつかの型に分けられるが，とくに生理的錯覚に属するものは数多くのものが存在する。これらの錯視は刺激対象が特別の形状や配置にあるとき，実際とは違った形や大きさ，性質のものに見えてしまう現象であって，だれにでもほぼ等しく起こりうるものである。

生理的錯視

（1）〈月の錯覚〉といわれるものは，月や太陽が地平線に近いときは中天にあるときよりも大きく見える現象であり，観察者の身体に対する方向関係から生じるもの，すなわち，身体の前方にあるものは見上げる方向にあるものより大きく見えると説明されている。

（2）明るさ，色の対比などに関しては，白，黄，緑のものは黒，赤，青のものより大きく見え（〈放散による錯視〉），色の色調や明るさは類似色が近くにあるときはいっそう似た色調や明るさに見え（〈同化による錯視〉），補色が近くにあるときはより際立って見える（〈対比による錯視〉）。

（3）物の運動に関する錯視としては，風が速く流れる夜空で月が雲の間を速く走って見えるように，あるものが動くと静止しているものが動いて見える〈誘導運動の錯視〉と，映画の原理のように，刺激を空間内の異なる位置に断続的に提示すると，その刺激が初めの位置から動いたように見える〈仮現運動の錯視〉がある。

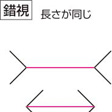
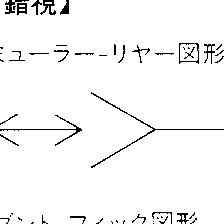
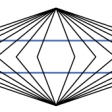
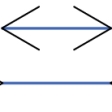
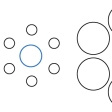
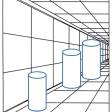
（4）〈幾何学的錯視〉といわれるものは，物の大きさ（長さ，広さ），方向，角度，形などの平面図形の性質が周囲の線や形などの関係のもとで実際とは違って見えるものである。たとえばミューラー・リヤー図形では同じ長さの直線がつけ加えられた矢線の影響で異なった長さに見えるものであって，外向矢線のついたほうが内向矢線のついたものより長く見え，ブント・フィック図形では，同長の垂直線と水平線が違った長さに見える。斜線が2本の平行線で中断されると，ずれて見えるポッゲンドルフ図形，縦の平行線が交差する斜線のために互いに傾いて見えるツェルナー図形は方向の変化の錯視である。ヘリング図形，ブント図形では，平行線が中央部で凸または凹に湾曲して見える。同心円の内円は過大視され，外円は過小視される（〈デルブフの大きさの錯視〉）ため，単独円と同心円の内円，および同心円の外円と単独円とは同じ大きさにもかかわらず異なって見える。ジャストロー図形では，同じ大きさの扇形でも内側のほうが外側のほうより大きく見え，また外側のほうが湾曲して見える。遠近法で描かれた絵の中の円筒（ポンゾ円筒）は手前に置かれて見える円筒よりも奥に置かれて見える円筒のほうが大きく見えるが，この絵を水平に近い方向から眺めて遠近法の効果を消すと，同じ大きさに見える。

（5）2種類以上に見える図形（多義図形）の一つの例としては〈シュレーダーの階段〉があり，階段に見えている図形がときおり斜上方から見たビル街に見えてくる。

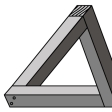
（6）矛盾図形の例としては〈ペンローズの三角形〉がある。図下のように上端が離れているときには立体に見えるが，その上端が密着して描かれている上の図は，現実にはそのような立体は存在しないにもかかわらず，ごくありふれた三角形の工作物と同じに見えてしまう。

（7）これらの生理的錯視は冷静な心理状態でも起こるが，特別の心理状態のとき起こる錯視がある。たとえば恐怖感の強いときに暗がりの中でススキの穂が揺れるのを幽霊と思うのは〈感動錯覚〉といわれ，冷静な心理状態になると消滅する。

病的な視覚性錯覚

視覚性錯覚のなかには病的状態のときに出現するものがある。たとえば振戦せん妄（しんせんせんもう）といわれる意識障害を伴うアルコール依存症などでは，床の上のごみや壁のしみが動く虫や襲いかかってくる怪獣に見えたり，赤い布切れが炎に見えるなど，活発な動きの感覚が加わって見える。特殊なものとしては，統合失調症などのさい出現するものがある。それには未知の人を知人と錯覚し，知人を未知の人と錯覚する一種の人物誤認があり，まただれを見ても敵がいろいろ変装しているのだと主張する〈フレゴリの錯覚〉，家人が本物ではなく替玉に見えてしまう〈ソジーの錯覚（替玉錯覚）〉といわれるものがある。
→錯覚
執筆者：中根 晃

図－錯視

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

錯視
さくし
visual illusion

視覚による錯覚のことで、明るさ、色、大きさ、長さ、形、方向、奥行、運動の錯視がある。錯覚の大部分は錯視である。錯視は、刺激を注意深く観察しても、またそれを熟知する人が観察しても明確に生じる。日常生活において、分量は小さくても、錯視と同様のずれや歪(ゆが)みを生じている場合が多いが、そのずれや歪みが顕著に生じる場合を錯視という。

　錯視はなんら特殊な異常な現象でなく、正常な知覚である。錯視の研究は、知覚全般を支配する一般原理を探るための有効な手段と考えられている。

　錯視を分類すると、幾何学的錯視、多義図形の錯視、逆理図形の錯視、月の錯視、対比錯視、運動の錯視、勾配(こうばい)の錯視、方向づけの錯視となる。

［今井省吾］

幾何学的錯視

大きさ（長さ・面積）、方向、角度、曲線などの平面図形の幾何学的関係が、物差しや定規によって測った客観的関係と食い違って見られる錯視現象である。多くの錯視図形には、発見者や考案者の名がつけられている。この錯視を便宜的に分類すると次のとおりである。

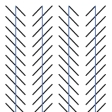
(1)角度方向錯視　ポッゲンドルフPoggendorff図形では、斜線がずれ、ツェルネルZöllner図形では、縦の平行線が互いに傾いて見られる。

(2)湾曲錯視　ブントWundt図形では、2本の平行線が湾曲して凹レンズ状に見える。

(3)大きさの錯視　ミュラー・リヤーMüller-Lyer図形では、矢線に挟まれた直線の長さは同じであるが、外側矢線条件のほうが内側矢線条件に比べ著しく過大視される。ヘルムホルツHelmholtzの正方形では、横縞(よこじま)で等分割された正方形は縦に長い長方形に見え、縦縞で等分割された正方形はやや横に長い長方形に見える。円環対比図形では、円環内の中央の円は左右同じ大きさであるが、左の円のほうが過大視される。ジャストローJastrow図形では、上下同じであるが、下のほうが過大視される。ポンゾPonzo円筒では、三つの円筒の大きさは同じであるが、遠方の円筒のほうが手前の円筒よりも過大視される。

　幾何学的錯視の規定条件や要因は多様であり、この錯視は予想以上に複雑な現象である。現在のところ、妥当な統一的説明理論は確立されていない。

［今井省吾］

多義図形による錯視

同一図形で2種以上の見え方が可能なもの。図と地の反転図形（ルビンRubinの杯と顔）や、遠近の反転図形（ネッカーNeckerの立方体）などがある。

［今井省吾］

逆理図形による錯視

矛盾図形、不可能図形。ペンローズPenroseの三角形のように、二次元的平面上に示される奥行の特徴を部分的に見れば解釈可能だが、まとめて知覚されると全体的形態は三次元的に不可能なように見られる図形である。

［今井省吾］

『W・メッツガー著、盛永四郎訳『視覚の法則』（1968・岩波書店）』▽『R・L・グレゴリー著、船原芳範訳『見るしくみ――目と脳の生理学』（1970・平凡社）』▽『R・L・グレゴリー著、金子隆芳訳『インテリジェント・アイ――見ることの科学』（1972・みすず書房）』▽『和田陽平・大山正・今井省吾編『感覚知覚心理学ハンドブック』（1969・誠信書房）』▽『今井省吾著『錯視図形――見え方の心理学』（1984・サイエンス社）』

[参照項目] | 運動知覚 | 錯覚

ポッゲンドルフ図形

ツェルネル図形

ブント図形

ミュラー・リヤー図形

ヘルムホルツの正方形

円環対比図形

ジャストロー図形

ポンゾ円筒

ルビンの杯と顔

ペンローズの三角形

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

錯視
さくし
optical illusion

物理的な計測手段ではかられた長さ，大きさ，角度，方向ないしはそれらの幾何学的な関係が，ある種の条件のもとで，それとは著しく食違って見える現象。視覚について現れる錯覚の一種であり，視覚的錯覚とも呼ばれる。その例としては，(1) 幾何学的錯視，(2) 月の錯視，(3) 反転錯視 (同一図形において2通りの見え方が交互に現れる現象をさし，ネッカーの立方体や反転図形の見え方がその例) ，(4) 運動の錯視，などがある。 (→運動知覚 ,　シャルパンティエの錯覚 )

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

錯視【さくし】

視覚における錯覚。平面図形の幾何学的関係，すなわち大きさ・方向・角度などに関する幾何学的錯視，同一図形において２種の知覚が交替的に現れる反転錯視，月や太陽が地平線近くで大きく見える月の錯視，白や黄色などの明色は暗色よりも大きく見える放散の錯視などがある。

出典　株式会社平凡社