日本大百科全書(ニッポニカ) 「重ね合せの原理」の意味・わかりやすい解説
重ね合せの原理
かさねあわせのげんり
ある物理量が時刻tにa(t)という値をとる現象があり、またb(t)という値をとる現象があるとき、それぞれに任意の係数λ、μを掛けて加えた和λa(t)+μb(t)を値とする現象も存在するなら、これらの現象に対して重ね合せの原理が成り立つという。線形な方程式の解は、この原理に従う。たとえば、光の波に対しては、この原理が成り立つ。それゆえ、光源Pからの光がスクリーン上の1点で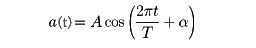
のように振動しているとき(tは時間、A、T、αは定数)、そこにPあるいは別のQから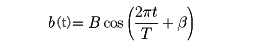
のように振動する光を当てると(Bとβも定数)、その点に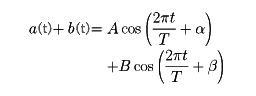
という光の振動がおこる。このとき、二つの波の位相がそろっていれば(すなわちα=βなら)二つの波の重ね合せは振幅A+Bをもつことになり、つまり、互いに強め合う。もしβ=α+180゜なら重ね合せは振幅|A-B|をもち、つまり弱め合う。このような強め合い、弱め合いをおこす重ね合せは干渉性があるという。これに対して非干渉性の重ね合せは、αとβが定数でなく時間とともに乱雑に変わる場合におこる。たとえば、αとβが0度になったり180度になったりすると、重ね合せの振幅はA+Bになったり|A-B|になったり乱雑に変動する。波の強さは振幅の2乗に比例するので
(A±B)2=A2+B2±2AB
の間を変動することになる。その平均値しか観測されないくらい変動が速ければ±2ABの項はみえず、重ね合わせた波の強さはaだけがあったときの強さA2とbだけのときの強さB2の単なる和にみえる。この場合、強め合いも弱め合いも全くおこらないため、非干渉性の波という。重ね合せの原理は空間座標の関数、あるいは広く時間と空間座標との関数に対しても同様に考えられる。波動に対しては、ほぼ一般に重ね合せの原理が成り立つ。たとえば、長い紐(ひも)をぴんと張って左端を振ると、そこから右端へと波が伝わっていく。その波が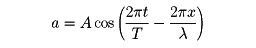
の形であったとする(xは紐に沿って左端から測った長さ、tは時間。波の周期がT、波長がλ)。同時に右端も振って、aの振幅が同じで反対向きに進む波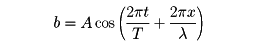
をおこすと、重ね合せの結果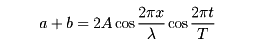
となる。これは紐の振動の形が、時間とともに変わらない波で、定常波とよばれている。重ね合せの原理が成り立たない波動は非線形波動とよばれる。
[江沢 洋]
『江沢洋著『力学』(2005・日本評論社)』
改訂新版 世界大百科事典 「重ね合せの原理」の意味・わかりやすい解説
重ね合せの原理 (かさねあわせのげんり)
superposition principle
principle of superposition
音波が伝わる空気中の密度の変化のように,場所(x,y,z)と時間tの関数として表される量f(x,y,z,t)が同次線形方程式となるときには,f1(x,y,z,t)という解とf2(x,y,z,t)という解があると,f1+f2も解になるという原理。重畳原理ともいう。光の波でも同様であり,2本の光束が交差する場所では両方の光による振動を重ね合わせたもの(光は電磁気力の波なのでベクトルとしての力の和)が各点の実際の振動になる。交わってからあとの各光束(例えばf2=0でf1≠0のところのf1)は,交わったことで何も影響を受けない。2本のホースから吹き出した水の噴流を交差させたような場合にはこのようなことはない。重ね合せは上の例のように主として波動で見られる現象で,波の干渉もその一つの例である。
執筆者:小出 昭一郎
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「重ね合せの原理」の意味・わかりやすい解説
重ね合せの原理
かさねあわせのげんり
principle of superposition
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の重ね合せの原理の言及
【地層累重の法則】より
…W.スミスによって始められた層位学の二つの基本法則の一つで,もし一連の岩石が他の岩石の上に重なっており,構造的に逆転などしていない場合には,上にのる岩石が新しいという意味である。相重なる二つの地層の空間的上下関係から時間的前後関係を読みとることができる。地層【加賀美 英雄】…
※「重ね合せの原理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
1 花の咲くのを知らせる風。初春から初夏にかけて吹く風をいう。2 ⇒二十四番花信風...

