数学的帰納法（読み）スウガクテキキノウホウ（英語表記）mathematical induction

デジタル大辞泉

すうがくてき‐きのうほう〔‐キナフハフ〕【数学的帰納法】

数学で、自然数nの命題が、n＝1のときに成り立ち、次にn＝kのときに成り立つと仮定して、n＝k＋1のときにも成り立つことを証明すれば、この命題は任意の自然数nについて成り立つという証明法。完全帰納法。

出典　小学館

精選版 日本国語大辞典

すうがくてき‐きのうほう ‥キナフハフ【数学的帰納法】

〘名〙 数学における証明法の一つ。自然数に関するある条件について、自然数１がその条件を満たす、自然数ｎがその条件を満たせば n+1 もその条件を満たす、という二つのことが成立するならば、いかなる自然数もその条件を満たすという原理に基づくもの。完全帰納法。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

数学的帰納法 (すうがくてききのうほう)
mathematical induction

個々の具体的事実から一般法則を導くことを論理学では帰納というが，数学的帰納法というのはそれとは多少異なり，次に示すような数学の証明法を意味する。

　例えば，1からnまでのn個の自然数の和S_nはn（n＋1）/2であるが，これを証明するのに次のようにしてもよい。

（1）n＝1のときは，S₁＝1，1×（1＋1）/2＝1ゆえ，S₁については正しい。

（2）n＝kのとき正しいとすると，S_k+1＝S_k＋（k＋1）＝k（k＋1）/2＋（k＋1）＝（k＋1）（k/2＋1）＝（k＋1）（k＋2）/2ゆえ，k＋1のときも正しい。

　このようにしてよい理由は，n＝kのときのS_k＝k（k＋1）/2という主張をP_kとしてみる。（1）はP₁は正しいことを示している。（2）はP_kが正しければP_k+1も正しいことを示している。（1）よりP₁が正しいのだから，（2）によりP₂も正しい。したがって（2）によりP₃も正しい，というようになり，すべての自然数nについてP_nが正しいことになるのである。

　一般に，命題の列P₁，P₂，……，P_n，……があって，自然数で番号づけられているとき，次の（1）（2）（3）いずれかができれば，すべてのP_iの証明ができることになり，これらの証明法を数学的帰納法というのである。

（1）（a）P₁は正しい，（b）P_kが正しければP_k+1も正しい，の2段階の証明。

（2）（a）P₁，……，P_rは全部正しい，（b）k＞rのとき，P_k-r，P_k-r+1，……，P_k-1が正しければ，P_kも正しい，の2段階の証明。

（3）kが自然数のとき，i＜kならばP_iはすべて正しいと仮定して，P_kの正しいことの証明。

　（1）は前出の例の場合である。（2）でもよいことは，同様の理由による。（3）は一段階節約したかのごとく見えるが，例えば，P₁を証明する場合，正しいと仮定されるものはないのだから，多くの場合P₁単独の証明が必要になるので，実際の証明としては，（1）の型が大部分であり，ときどき（2）の型になる場合がある。まれにP₁のためにとくに別のいいまわしをすることなく，ほんとうに（3）の一段階だけですむことがある。

　もっと一般な場合もある。すなわち，極小条件を満たす順序集合Mで番号づけられた命題P_m（m∈M）の集りがあって，上の（3）と同様に，各m∈Mについて，〈n∈M，n＜mならばP_nは正しい〉との仮定の下で，P_mの証明ができれば，すべてのP_mが正しいことになる。なぜなら，正しくないP_mがあったとして，A＝｛m∈M｜P_mは正しくない｝をとると，極小条件は，Aに極小元αがあることを意味する。n＜αならP_nは正しいのだから，P_αも正しいはずでα∈Aに反する。

　この証明法も数学的帰納法の一種とされるが，超限帰納法を特別な場合として含んでいる。
執筆者：永田 雅宜

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

数学的帰納法
すうがくてききのうほう
mathematical induction

自然数上の変数を含む命題に対し、自然数のある性質に着目して、その命題を証明、あるいは定義するための手法をいう。p(x)を自然数xについての述語とするとき、自然数の性質として、「p(1)が成り立ち、かつ、任意の自然数kについてp(k)ならばp(k＋1)である、が成立すれば、すべての自然数nについてp(n)である」が成り立つことが知られている。このことを用いた証明あるいは定義が、数学的帰納法による証明であり、数学的帰納法による定義（帰納的定義）である。

　たとえば、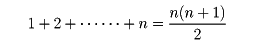

が成立することの証明には、「n＝1のときには、左辺、右辺とも1となって成立する」。さらに、「n＝kのとき成立すると仮定すると、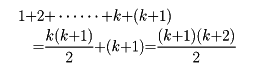

となって、n＝k＋1の場合も成立する」ことで十分である。

　次に、ある数列｛a_n｝を数学的帰納法によって定義してみよう。n＝1のとき、a_nを1、すなわち、a₁＝1と定義し、n＝kのときa_kが定義されていると仮定して、n＝k＋1のとき、a_k+1＝a_k・(k＋1)と定義する。このような帰納法による定義は、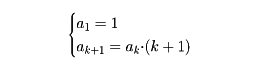

と書くのが普通である。この定義による数列は、
　　a₁＝1, a₂＝1・2＝2, a₃＝2・3＝6,
　　a₄＝6・4＝24, a₅＝24・5＝120, ……,
　　a_n＝1・2・3・4・……・(n－1)・n(＝n！),……
となる。この方法によって数列｛a_n｝が定義されていることは、「数列の第n項a_nが定義される」という命題p(n)を考えてみればよい。

　数学的帰納法には、「任意の自然数kについて、m≦kなるすべての自然数mに対しp(m)ならばp(k＋1)である、が成立すれば、すべての自然数nについてp(n)が成立する」など、いろいろな形式のものがある。なお、数学的帰納法は、その形式が「帰納」にきわめて似通っていることからきた名称で、内容は、対象のすべてを調べるのであるから、「演繹(えんえき)」の一種である。このため、完全帰納法ともよばれる。

［廣瀬　健］

[参照項目] | 自然数

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

数学的帰納法
すうがくてききのうほう
mathematical induction

自然数 n についてのある命題 A(n) において，A(1) は真である，ある任意の自然数 s について A(s) が真であると仮定すれば A(s＋1) もまた真である，という2つのことが証明されれば，A(n) はすべての自然数 n について真であるという推論が成り立つ。この推論を数学的帰納法あるいは完全帰納法といい，自然数全体の集合を定義したペアノの公理系の第5公理を基礎に導かれる論法である。そこでペアノの第5公理を数学的帰納法の公理と呼ぶ。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

数学的帰納法【すうがくてききのうほう】

完全帰納法とも。自然数nを含む命題P（n）について，1.P（１）は真である，2.P（k）が真であると仮定すればP（k＋１）も真である，の二つが証明されれば，P（１），P（２），P（３），…が真であることを順に証明でき，したがってP（n）がすべての自然数nについて真であることが証明される。このように1.と2.を証明することにより全自然数に対する一般的証明を得る方法を数学的帰納法という。→帰納／演繹

出典　株式会社平凡社