ハミルトン関数 (ハミルトンかんすう)
Hamiltonian function
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
ハミルトン関数
はみるとんかんすう
Hamilton's function
座標と運動量の関数で、ある物理系の力学的特性を表しその運動を規定する量。イギリスの数学者・物理学者のW・R・ハミルトンが導入(1828、32)。保存力のみ働き拘束条件が時間を含まない場合には、系の運動エネルギーとポテンシャルエネルギーの和、すなわち系の全エネルギーを表し、力学的エネルギー保存則はこの関数の値が時間的に変わらないことを意味する。ハミルトン関数に基づく運動方程式をハミルトンの正準方程式、それから出発する力学の形式をハミルトン形式とよぶ。その内容はニュートンの運動方程式と同等であるが、この形式では座標と運動量がともに独立変数で、両者を含む適当な座標変換に対して正準方程式の形が変わらないようにできる。そのような変換を正準変換という。
正準方程式は量子力学のハイゼンベルク方程式に対応するもので、古典力学から量子力学への移行に重要な役割を演じた。自由度fの力学系のハミルトン関数をH、一般化座標とそれに共役な運動量を(qi,pi)i=1,2,……,fとすると、正準方程式はラグランジュ方程式を変形することによって、次のような2f個の連立一階偏微分方程式として得られる。
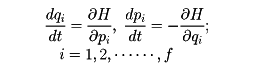
[永田 忍]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
ハミルトン関数
ハミルトンかんすう
Hamilton function
力学系の一般座標を qi(i=1,2,…,f) ,一般速度を 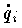 ,一般運動量を pi ,ラグランジュ関数を L とするとき,次の qi,pi,t の関数をハミルトン関数という。
,一般運動量を pi ,ラグランジュ関数を L とするとき,次の qi,pi,t の関数をハミルトン関数という。
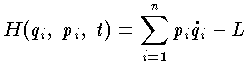 保存力場において,H が t を含まないときには,H は全エネルギーを表わし,H=T+V である。ここで T は運動エネルギー,V はポテンシャルエネルギーを表わす。 H を用いてハミルトンの正準方程式が導き出され,力学系の運動が決められるから,H は力学系を規定する基本的な量である。量子力学では,H はハミルトニアンと呼ばれることが多い。
保存力場において,H が t を含まないときには,H は全エネルギーを表わし,H=T+V である。ここで T は運動エネルギー,V はポテンシャルエネルギーを表わす。 H を用いてハミルトンの正準方程式が導き出され,力学系の運動が決められるから,H は力学系を規定する基本的な量である。量子力学では,H はハミルトニアンと呼ばれることが多い。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内のハミルトン関数の言及
【アイコナル】より
…この関数V(P0,P)をアイコナルと呼ぶ。実質的にはW.ハミルトンが初めて導入したものであるが,その業績がうずもれてしまい,のちにH.ブルンスがそれとは独立に再発見した(1895)。アイコナルは解析的に幾何光学的結像を論ずるので便利であり,これを記述する独立変数としては,位置座標P0(x0,y0,z0),P(x,y,z)の組のほかに,光線の方向余弦にそれぞれの空間の屈折率をかけた光学的方向余弦(p0,q0,r0)と(p,q,r)をとることもできる。…
【四元数】より
…複素数の一つの拡張として,W.R.ハミルトンによって考えだされた数である。四元数αは2乗して-1になる三つの数i,j,kによって, α=a+bi+cj+dk (a,b,c,dは実数) と表され,二つの四元数α,α′(=a′+b′i+c′j+d′k)の和は, α+α′=(a+a′)+(b+b′)i +(c+c′)j+(d+d′)kで定められる。…
【数学パズル】より
…図17‐aはアーレンスW.Ahrens著の《数学遊戯》第2巻(1918)にある問題で,かなり複雑そうに見えるけれども,A点とB点だけが奇数の点であることを確認すれば図17‐bのような解が簡単に得られる。一筆書きと似たトポロジーパズルにハミルトン閉路の問題がある。W.R.ハミルトンが考えたもので,その結果を1859年に報告している。…
【ハミルトンの原理】より
…このように運動方程式そのものが運動法則をもっとも直接に表すのであるが,19世紀になって,これを別な形に述べることによってより統一的な原理にまとめる試みが次々と現れ,それを軸としてニュートン力学は解析力学にまとめられるようになった。そのような試みとして[ダランベールの原理]や[最小作用の原理]の例があげられるが,そのうちもっとも一般的で完全なものが1834年W.R.ハミルトンによって与えられたハミルトンの原理であり,解析力学の基本原理となっているものである。ハミルトンの原理は以下のように述べられる。…
※「ハミルトン関数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
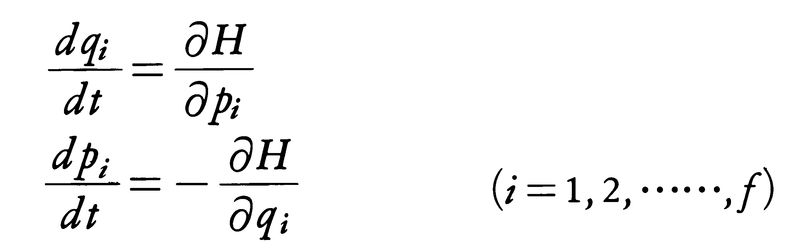
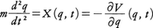 は,ハミルトン関数,
は,ハミルトン関数,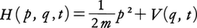 から正準方程式,
から正準方程式,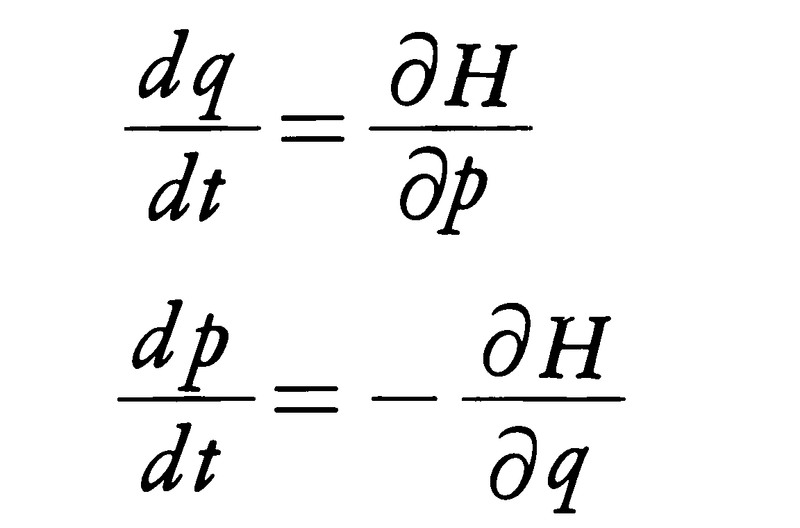
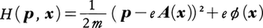 で与えられるが,これは荷電粒子の(電磁場との相互作用を含む)エネルギーを表し,これに電磁場固有のエネルギーを表すハミルトニアンを加えたものが全系のもつエネルギーのハミルトニアンを与えることとなる。
で与えられるが,これは荷電粒子の(電磁場との相互作用を含む)エネルギーを表し,これに電磁場固有のエネルギーを表すハミルトニアンを加えたものが全系のもつエネルギーのハミルトニアンを与えることとなる。

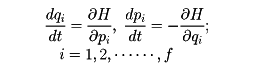
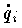 ,一般運動量を pi ,
,一般運動量を pi ,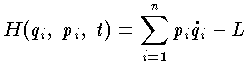 保存力場において,H が t を含まないときには,H は全エネルギーを表わし,H=T+V である。ここで T は運動エネルギー,V はポテンシャルエネルギーを表わす。 H を用いてハミルトンの
保存力場において,H が t を含まないときには,H は全エネルギーを表わし,H=T+V である。ここで T は運動エネルギー,V はポテンシャルエネルギーを表わす。 H を用いてハミルトンの