ラグランジュ関数（読み）ラグランジュかんすう（その他表記）Lagrangian function

改訂新版　世界大百科事典

ラグランジュ関数 (ラグランジュかんすう)
Lagrangian function

一般に物理的な体系が時間または空間的に変化する法則は変分原理によって表現されることが多いが，その場合対象となる系の物理量を含む汎関数でその積分が変分汎関数となるものをラグランジュ関数と呼び，一般にLで表す（ここで物理量の汎関数とは，物理量自体時空変数の関数として表されるので関数の関数という意味で用いられる用語である）。以下，質点の力学の場合について具体的に説明しよう。物理量x（t）（x₁（t），……，x_n（t））に関する時間tの2階常微分方程式，

　\(\frac{d^2x}{dt^2}\)＝f（x，t）　……（1）　

として運動法則が表される場合，適当な関数L（x，ẋ，t）が定められて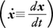，変分汎関数，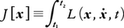

の停留条件（変分原理），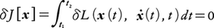


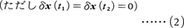
を満たすx（t）のみが上の運動法則に従うとなっているならば，先の運動法則（1）は変分原理（2）で置き換えられたことになる。その結果，運動法則を個々の場合に応じて（1）の形に述べる代りに変分原理（2）によって統一的に示すことができるという利点が生ずるわけである。変分原理（2）から運動法則（1）が導かれるような関数L（x，ẋ，t）が，運動方程式（1）のラグランジュ関数と呼ばれるものであり，変分法の一般論からその場合の運動方程式はオイラーの方程式，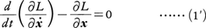

である。J.L.ラグランジュは最初いわゆる等周問題についてこの方程式を考察し，次いでニュートンの運動方程式に適用して解析力学の基礎を築いた。すなわちポテンシャルU（x）のもとで運動する質点（質量m）に対しては，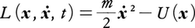

を用いることによりオイラーの方程式（1′）がニュートンの方程式，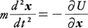

に一致することがわかる。一般にq₁，……，q_fの関数としてのポテンシャルU（q，t）のもとで運動する力学系では，速度q_iの正値二次形式として運動エネルギーTが与えられるならば，

　L（q，q，t）＝T（q，q）－U（q，t）

であって，この場合の変分原理（2）は力学法則を変分原理で表す先駆となった仮想変位の原理またはダランベールの原理と等価なものであることが知られる。ラグランジュ関数は座標qの一次までの微係数を含むスカラー関数であるから，変数の変換により座標系を変更して取り扱うのに便利である。実際オイラーの方程式（1′）は座標の選び方によらぬ形式である（これに対しLを用いない運動方程式を直接変数変換すると，多くの場合非常に複雑となる）。

　さて，解析力学に現れる上述のラグランジュ関数の場合，積分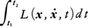は作用積分の名で呼ばれ，運動方程式の解である軌道に沿っての積分ならば，積分結果は作用S（x（t），t）の両端値の差S（x（t₂），t₂）－S（x（t₁），t₁）に等しい。20世紀に至って量子力学が誕生し，波動関数とこの作用積分との関係が永く論ぜられているが，1948年R.P.ファインマンは経路積分を導入して波動関数を古典力学の軌道群によって表現することを提案した。その経路積分には，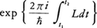

の形式で作用積分が登場する（ℏはプランク定数を2πで割ったもの，またi²＝－1である）。
執筆者：長谷川 洋

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ラグランジュ関数
らぐらんじゅかんすう
Lagrange's function

座標とその時間微分の関数で、ある物理系の力学的特性を表し、その運動を規定する量。フランスの物理学者・数学者ラグランジュが導入した。この関数に基づく運動方程式をラグランジュ方程式といい、その内容はニュートンの運動方程式と同等である。ラグランジュ関数をLとすると、系の運動エネルギーTとポテンシャルエネルギーUによりL=T-Uと定義される。Lと初期条件が与えられると系の全運動が記述されるので、これから出発する力学の形式をラグランジュ形式とよび、解析力学の基本的な体系となっている。

　ニュートン力学の場合のみならず、電磁場中での荷電粒子の運動や相対論の場合の運動方程式もラグランジュ形式に書くことができ、一般性の高い枠組みであると考えられる。自由度fの系の位置を一義的に定める一般化座標を(q₁,q₂,……,q_f)とすると、Lはこの座標とその時間微分

および、より一般的には時間tによって表される。力学系の運動を与えるハミルトンの原理はLの時間積分に対する変分原理で、一般化座標で変分を行うことにより次のラグランジュ方程式を得る。

これは一般化座標に対する運動方程式であり、その形は座標変換をしても変わらない。

［永田　忍］

[参照項目] | 解析力学 | ハミルトンの原理

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

ラグランジュ関数
ラグランジュかんすう
Lagrange function

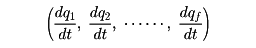
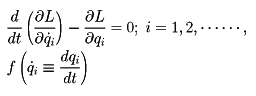
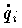ラグランジアンともいう。ニュートン力学において保存力が働くとき，運動エネルギー T とポテンシャルエネルギー V との差 L＝T－V で与えられる関数のこと。L は一般座標 q_i(i＝1，2，…，f) と一般速度 との関数であって，これからラグランジュの運動方程式が導き出され，系の運動が決まる。したがって，ラグランジュ関数は力学系を規定する基本的な量である。連続体の力学，電磁場や一般の場に対しても L に相当する量を考えることができ，この量はラグランジュ関数密度と呼ばれる。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

ラグランジュ関数【Lagrangean】

運動エネルギー T とポテンシャルエネルギー V の差を L で表し，これをラグランジュ関数（ラグランジュアン）という．自由度の数が有限な系を取り扱うには便利な関数である．

出典　朝倉書店