超越数（読み）チョウエツスウ

デジタル大辞泉

ちょうえつ‐すう〔テウヱツ‐〕【超越数】

代数的数でない数。自然対数の底ていe、円周率πパイなど。有理数を係数とする代数方程式の解として表すことができない。

出典　小学館

精選版 日本国語大辞典

ちょうえつ‐すうテウヱツ‥【超越数】

1. 〘 名詞 〙 有理数係数の代数方程式の根となることのできない複素数。自然対数の底(てい)、円周率など。
   1. [初出の実例]「代数的数でない数には超越数といふ名を与へてゐる」(出典：雫の発見（1939）〈吉田洋一〉直線を切る)

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

超越数
ちょうえつすう

代数方程式の解とはならない数を超越数という。一変数で整係数の方程式を（一変数）代数方程式ということにする。つまり
　a₀xⁿ+a₁x^n-1+……+a_n-1x+a_n=0
　(a₀,a₁,……,a_nは整数でa₀≠0)
の形の方程式が代数方程式である。nをその方程式の次数という。ある代数方程式の解となる複素数（実数の場合を含む。以下同様）を代数的数という。たとえば、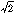,,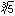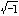はそれぞれ
　x²-2=0, x³-5=0, x²+1=0
の解だからいずれも代数的数である。またすべての有理数は代数的数である。しかるに、円周率π、自然対数の底e、また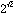はどんな代数方程式の解にもならないことが証明される。このような複素数が超越数である。

　一般に実数は有理数と無理数に分類されるが、無理数はさらに実の代数的数と実の超越数とに分類されることになる。代数的数の全体は可算無限個であるが、実数の全体は非可算だから、超越数の全体も非可算である。つまり超越数のほうが、代数的数より圧倒的に多い。近年、イギリスのベーカーAllan Baker（1939―　）によって、それまでに得られた定理の多くを包合する次のような著しい定理が得られた。α₁、……、α_nを1でも0でもない複素数とし、1、β₁、……、β_nを有理数体上一次独立な代数的数とすると、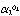……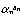は超越数である。これにより、前述のπ、e、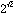のほか、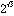,,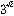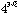などが超越数となることが、ただちに知られる。

［足立恒雄］

[参照項目] | 代数方程式

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

超越数 (ちょうえつすう)
transcendental number

有理数係数のどんな代数方程式についてもその根にならない数，すなわち代数的数ではない数を超越数という。有理数から代数的操作で得ることができないという意味でL.オイラーが超越数と名付けた。彼は1748年ころ自然対数の底e，円周率πなどは超越数であろうと予想したが，eが無理数であることしか証明できなかった。1844年，J.リウビルは，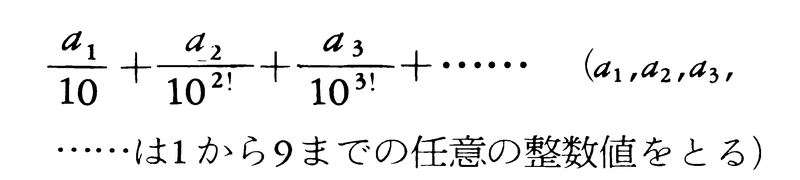

は超越数であることを示し，超越数が無限にあることを初めて証明した。その後，G.カントルは集合論を建設し，濃度の概念を用いて超越数は代数的数よりはるかに多いことを77年に示してセンセーションを巻き起こした。しかしながら，具体的に与えられた数が超越数であるかどうかを判定することは今日でもきわめて困難な問題である。1873年，C.エルミートはeが超越数であることを示し，82年，リンデマンLindemannはπが超越数であることを示した。これによって超越数への関心が高まり，1900年，D.ヒルベルトはパリの国際数学者会議で23の問題を提出したが，そのうちの7番目で次のような超越数の問題をあげている。〈α（≠0，1）が代数的数で，βが代数的数であってしかも無理数のときには，α^βは超越数であるか。例えば2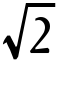，e^π＝i⁻²ⁱは超越数か〉。これは34年I.M.ゲルファントとシュナイダーSchneiderによって独立に解決され，今日の超越数の理論の基礎になっている。しかしながら，オイラーの定数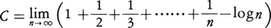，は超越数であることが予想されているが，無理数であるかどうかもわかっていない。超越数の理論はディオファントス近似（無理数を有理数で近似する問題）と密接に関連している。θを無理数とすると，任意の正の数k＞2に対して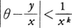を満足する整数x，yの個数は有限であることを54年にロスRothが証明した。この結果は超越数の理論で重要な役割をもつ。今日，ベーカーBakerをはじめとする多くの数学者により，ディオファントス近似の研究とその超越数の理論への応用が活発に行われている。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

超越数【ちょうえつすう】

有理数を係数とするいかなる代数方程式の根ともなり得ない数。たとえば（式１）は無理数であるがx²−２＝０の根だから超越数ではない。円周率πや自然対数の底eは超越数である。実数または複素数の中で，超越数でないもの（代数的数）は可算個しかなく，この意味で，実数，複素数の大部分は超越数である。
→関連項目エルミート｜カントル｜リウビル

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

超越数
ちょうえつすう
transcendental number

代数的無理数でない無理数，すなわち有理数を係数にもつ代数方程式の根とはなりえない無理数のことである。たとえば，円周率 π＝3.14159… ，自然対数の底 e＝2.71828… ，10の累乗を除く整数の常用対数，θ° ( θ は整数値) の角の三角関数の大部分などは超越数である。超越数の存在は，J.リュービルによって，1831年に初めて証明され，e が超越数であることは，73年に C.エルミートによって，π が超越数であることは，82年に F.リンデマンによって証明された。なお 74年に，G.カントルは超越数は代数的数より多く存在することを示した。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の超越数の言及

【数体】より

…代数的数全体も数体であるが，これは，いわゆる無限次拡大体であって，上のような形では得られない。複素数であって，代数的数でないものを超越数という。自然対数の底eや円周率πは超越数である。…

【無理数】より

…自然数aが他の自然数のn乗で表せないときⁿは無理数であり，この形の無理数を不尽根数という。また，無理数の中には自然対数の底eや円周率πなどのように超越数と呼ばれるものもある。無理数は小数で表すと，循環しない無限小数で表されるが，逆に循環しない無限小数は無理数である。…

※「超越数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」