ロッシュの限界（読み）ロッシュのげんかい（その他表記）Roche's limit

改訂新版　世界大百科事典

ロッシュの限界 (ロッシュのげんかい)
Roche's limit

惑星がその近くの衛星に及ぼす潮汐作用についての本来の意味（1）のほか，近接連星のロッシュ・ローブRoche's robeの意味（2）でも使われる。

（1）球型の惑星のまわりを円運動する衛星を考える。衛星は一様な密度の均質な流体からなるものとする。衛星の形はおもに自己重力によって決まるが，自転の遠心力とか惑星の潮汐力も影響する。さて，衛星の円軌道の半径がゆっくりと減少して衛星がしだいに惑星に接近したとすると，衛星の形は3軸不等の楕円体となり，その最長軸をつねに惑星に向けた状態が安定になる。さらに惑星に近づくと軸比が長軸：中軸：短軸＝1.59：0.82：0.77の形に近づく。しかしそれが限度であって，このときの惑星からの距離rは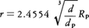，で与えられる。ここにd_Pは惑星の平均密度，dは衛星の密度，R_Pは惑星の半径である。衛星がこの距離よりさらに惑星に近づくと衛星は一定の形を保てなくなる。多分小さな流体塊に分裂するだろう。よって上記のrをロッシュの限界（距離）という。ロシェÉdovard Albert Roché（1820-83）が1850年に求めた関係だが，上式の係数2.4554はG.H.ダーウィンの再計算によるものでロシェは2.44とした。

　衛星が岩石からなる場合でもその形状が自己重力で保たれるくらい質量が大きければ流体の場合と同じに扱ってよい。その質量の目安は（重力ポテンシャル）≅（分子間引力のポテンシャル）で与えられる。改めて衛星を均質な球体としてCGS単位で質量，半径，密度をそれぞれM，R，dとすると，衛星の自己重力のポテンシャルは3/5GM²/Rで与えられるから，単位質量当りでは3/5GM/R（erg/g）となる。一方，きわめて単純に岩石をSiO₂分子（分子量60）が分子間引力で結合したものと考え，結合力のポテンシャルを1分子についてη（eV）（＝1.6×10⁻¹²ηerg）とすると，単位質量では1.6×10¹⁰η（erg/g）となる。ゆえに3/5GM/R≅1.6×10¹⁰ηと考え，M＝4/3πR³dを使って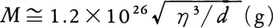，の関係が導かれる。ところで一般に化学反応で出入りするエネルギーは1～10eVとされる。このエネルギーは化学反応にあずかる分子を分解，合成するほどの量であり，今の場合，分子自身はそのままで分子の集合体と考えた岩石を分裂させる程度のエネルギーは1eVより少なくてよい。そこでηを0.01～0.1とおいてみると，d＝3として臨界質量はM^＊＝7×10²²～2×10²⁴gとなる（R^＊＝200～600kmに相当）。つまり衛星の質量が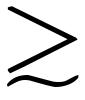M^＊ならロッシュの限界は固体衛星にも通用する。しかし衛星の質量が小さくて形状が自己重力よりも分子間引力（物性力）で保たれる場合にはロッシュの限界は意味を失う。実際あらゆる人工物体がそうであって，地球の表面あるいはその近傍の空間（ロッシュ限界内）に安全に存在している。

　なお，均質球状天体での関係，すなわちM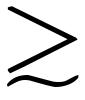M^＊ならば重力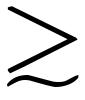物性力は，ロッシュの限界の問題を離れて小天体の形状の問題にも適用される。つまり形状が不規則な天体は自己重力がきいていないからその質量はM^＊より小さいものに限られる。

（2）一般に恒星の質量は中心部に集中している。そこで近接連星の主星と伴星の質量が極端な中心集中度をもつと考えると，それぞれの星の重力ポテンシャルは質点のそれと同じになる。ゆえに，共通重心のまわりに円運動をする近接連星の等ポテンシャル面は，制限三体問題の零速度曲面と一致する。このとき両星の中心を結ぶ線分上のラグランジュ点L₁を通る等ポテンシャル面をロッシュ・ローブ，あるいはロッシュ限界（面）という。ロッシュ・ローブは主星と伴星のそれぞれを囲む二つの卵形閉曲面がL₁で接した形をしていて，近接連星の進化を論ずるのに欠かせない概念である。
執筆者：堀 源一郎

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

ロッシュの限界
ロッシュのげんかい
Roche limit

ある程度以上の大きさをもった惑星ないし衛星が，一定の距離以上に主星に近づくと，潮汐力のために破壊されてしまう。この距離をロッシュの限界といい，衛星が流体状で，しかも主星と衛星の密度が同じ場合には，主星の中心からその半径の約 2.44倍にあたる。土星の環のいくつかは土星の半径の 2.3倍以内に収まっているので，衛星が破壊されてできたものである可能性が大きい。木星の環も，木星の半径の 1.8倍以内に収まっている。木星の第5衛星アマルテアは，この限界すれすれの外側を公転している。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のロッシュの限界の言及

【近接連星】より

…単独星ならどんどん膨張して巨星や超巨星になっていくが，近接連星では質量の大きいほうがまず進化的膨張により図1でW₂→W₁→W₀と大きくなっても，W₀面以上には膨張できない。W₀面は空中にできた目に見えない壁のようなもので，ロッシュの限界と呼ばれる。このロッシュ限界面では，両星のまわりの二つのポテンシャル面は中間のL点(ラグランジュ点)で接触してしまうという特徴をもつ。…

※「ロッシュの限界」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」