円運動（読み）エンウンドウ

デジタル大辞泉

えん‐うんどう〔ヱン‐〕【円運動】

円周に沿って動く物体の運動。

出典　小学館

精選版 日本国語大辞典

えん‐うんどうヱン‥【円運動】

1. 〘 名詞 〙 定まった円周に沿って回る運動。速さが一定のときは等速円運動という。〔物理学術語和英仏独対訳字書（1888）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

円運動
えんうんどう

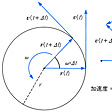
質点が平面上の一つの円周上を回る運動のこと。図のように円運動では、速度の方向が各瞬間で円の接線方向であり、中心からの位置ベクトルの方向といつも直交している。したがって円運動を行っている物体では、絶えずその速度の向きが変化していて、速度の時間変化すなわち加速度が存在する。ニュートンの法則によって、円運動をしている物体にはこの加速度を生じさせている力が外から作用しているはずである。一定の速さvで回る等速円運動の場合、加速度ベクトル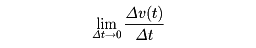

は、いつも中心に向かっているので、向心加速度とよばれ、それに比例する（質量mを比例係数として）外力もまた中心に向いている。その大きさは、ベクトル図を参考にして容易に求められ、角速度をωとすれば、mvωである。円軌道の半径をrとすると、v＝rωの関係を用いて、mv²/rで表される。これを向心力または求心力という。

　このように、物体に円運動を続けさせるためには、絶えず向心力を作用させなければならない。たとえば、「おもり」を「ひも」で結び、回転させると、「おもり」は絶えず中心から遠ざかろうとするが、これに抗して円運動を続けさせるためには、絶えず「ひも」を引っ張っていることが必要である。これは「ひも」を通じて向心力を作用させていることになる。なお、中心から遠ざかろうとする傾向は見かけの力、遠心力が働いていると考えることができる。もちろん向心力としては、かならずしも「ひも」を用いて引っ張る必要はない。ニュートンの万有引力や、プラスとマイナスの静電気をもつ粒子の間に働くクーロン力でもよい。これらの力のもとで物体は一般に放物線、双曲線または楕円(だえん)軌道上を運動する。円運動は楕円軌道の長軸と短軸とが等しい場合である。実際、万有引力の作用のもとで運動している太陽系の惑星は、太陽の周りの円に近い楕円軌道上を運動していることが知られている。また人工衛星は、月と同様、地球の引力の作用のもとでの円に近い楕円軌道上の運動をしている。

［阿部恭久］

円運動〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

円運動 (えんうんどう)
circular motion

一つの円周に沿ってまわる運動。速さが一定でも，円運動では速度の方向が絶えず変化するので加速度が存在する。円の半径をR，速さをVとすると，等速円運動の加速度はつねに円の中心に向かい，その大きさはV²/Rに等しい。この加速度を与え続けて，質量mの物体に上記の等速円運動をさせるためには，中心へ向かう，大きさmV²/Rの力が必要である。これを向心力または求心力という（遠心力）。

　アリストテレスは，運動の基本形は直線運動と円運動であり，永続可能なのは円運動であるから，円運動こそもっとも完全な運動であると論じた。その影響は中世を通じて根強く残り，惑星の運動を円運動の組合せで表そうというプトレマイオスの天動説が永く宇宙観を支配した。地動説を唱えたガリレイもなお円運動には拘泥していたといわれ，ケプラーにいたってようやく完全に円運動から脱却することができた。
執筆者：小出 昭一郎

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

円運動【えんうんどう】

質点が円周上を回る運動。角速度ωが一定な等速円運動（円の半径r）では，速度はrω（接線方向），加速度はrω²（中心に向かう）となる。→遠心力／向心力

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

円運動
えんうんどう
circular motion

物体が1つの円周上を回る運動。速さが一定な等速円運動では，中心のまわりの角速度が一定であり，また加速度も一定で円の中心に向い，したがって物体には円の中心に向う一定な大きさの向心力が作用する。質点の等速円運動を直線上に正射影すると，射影点は単振動をする。

出典　ブリタニカ国際大百科事典 小項目事典