カルダーノ（読み）かるだーの（その他表記）Girolamo Cardano

デジタル大辞泉

カルダーノ（Girolamo Cardano）

［1501～1576］イタリアの数学者・医者・哲学者。カルダーノの公式とよばれる三次方程式の根の解法を発表。

出典　小学館

精選版 日本国語大辞典

カルダーノ

1. ( Girolamo Cardano ジロラモ━ ) ( [ラテン語] Hieronymus Cardanus ) イタリア、ルネサンスの数学者、医師、哲学者。代数方程式の理論を開拓。（一五〇一‐七六）

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

カルダーノ
かるだーの
Girolamo Cardano
（1501―1576）

イタリア・ルネサンス期の医学者、自然主義的哲学者、数学者。ミラノ近くのパビアに私生児として生まれ、母親の不安定な愛情のため、悲しい少年期を送る。パビア、ミラノ、パドバで学び、パビア、ミラノ、ボローニャで医学を教える。いわゆる「カルダーノの公式」によって数学者として広くヨーロッパに知られた。70歳で投獄、異端審問にかけられるが、晩年はローマで過ごした。

　その特異な性格は、1542年に書かれ死後出版された『自伝』（1643）にうかがわれる。きわめて旺盛(おうせい)で広範な知識欲をもち、占星術、魔術などに関する著作のほか、とくに哲学的な主著としては、百科全書ともいうべき『不思議について』（1550）、『事物の雑多について』（1557）があり、そこにはルネサンスに固有な矛盾が典型的な形で現れている。アニミズム的立場から、一方では新プラトン主義的伝統に従って、魔術のもつ思弁的価値を認めながら、他方、物質自体のなかに生命の原理をみいだし、人間を頂点とする進化論的な考えをとる。そのためアリストテレスに反し、物質に活動的な特徴を認めることによって、内在論的・進化論的自然観へと向かう一方、自然の絶対的な一つとしてのまとまりを、霊という超自然的原理に求めざるをえないことから、超越論的自然の形而上(けいじじょう)学にもなっている。人間の霊魂についてアベロエス（イブン・ルシュド）的解釈をとる。

［大谷啓治］

　1545年に『すばらしい技術、すなわちアルゲブラの規則について』Artis magnae, sive de regulis algebraicisを出版、このなかに三次方程式における「カルダーノの公式」がある。この方法はタルターリア（フォンタナ）が樹立した公式で、彼がカルダーノに、他人に教えないことを条件として教えたのであるが、その約束を破って上記の著書に公表してしまい、発表者の名をつける習慣から「カルダーノの公式」と名づけられた。カルダーノの公式は、その当時には式はなく、ことばで示されているが、現代の式で示すと、三次方程式x³＋px＝qの根が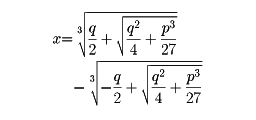

であることを示したものである。

［小堀　憲］

『カルダーノ著、青木靖三・榎本恵美子訳『わが人生の書――ルネサンス人間の数奇な生涯』（1980・社会思想社／1989・現代教養文庫）』▽『清瀬卓・澤井繁男訳『カルダーノ自伝』（1995・平凡社）』

[参照項目] | イブン・ルシュド | 三次方程式 | フォンタナ

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

カルダーノ
Girolamo（Geronimo） Cardano
生没年：1501-76

イタリアの医学者，自然哲学者，数学者。占星術や魔術にも造詣が深かった。法律家で，数学にもたしなみのあったF.カルダーノの庶出児としてパビアに生まれた。1526年にパドバ大学で医学博士となり，開業したが，初めの10年近くはほとんど患者もつかず，極貧の生活を送った。また青年時代には長らく性的に不能であった。しかしその後しだいに名医としての評判が高まり，ミラノ，パビア，パドバの各大学で医学教授を歴任するかたわら，有力な貴族たちから診察を求められた。イギリスまで出向いて，スコットランド大司教の喘息を治療したこともある。50年代には，自然哲学に関する大著《微細なる事物について》（1552）と《さまざまな事物について》（1556）を著し，思想家としてヨーロッパ全体で広く注目を沿びた。晩年には，その占星術的な観念に関して異端審問所の嫌疑を受けて一時入牢したが，釈放されるや，数奇に満ちた生涯を回想して，《自叙伝》の執筆にふけった。カルダーノの学問的業績として歴史的に見て最も高く評価されるのは，代数学の研究である。古代ギリシアから15世紀末まで3次方程式の解法は不可能であると信じられてきたが，16世紀になるとS.dalフェロScipione dal（del） Ferro，タルターリア等はその特殊な解法を発見した。しかし彼らはいずれもその秘密を公開することはなかった。これに対してカルダーノは，タルターリアから得たわずかな示唆を手掛りにして，今日〈カルダーノの公式〉と呼ばれる三次方程式の一般的解法を見いだし，それを幾何学的に証明するとともに，従来の代数学を体系的に再考察し，そのさまざまな基本的性質を導出した。これらの画期的な成果は，彼の弟子L.フェラリの得た4次方程式の解法とともに1545年に《大技法》として出版され，近代的な代数学形成のための大きな原動力となった。また，パスカルやフェルマーによって展開される確率論の先駆的業績を残したことも注目される。
執筆者：横山 雅彦

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

カルダーノ
Cardano， Geronimo

[生]1501.9.24. パビア
[没]1576.9.21. ローマ
イタリアの数学者，医者。 1526年にパドバ大学で医学の学位を取り，43年にはパビアで医学教授の地位を獲得。初めて発疹チフスの症状を医学的に記述するなど，医者としての名声も高かった。数学者としては，当時の第一人者であり，現在『アルス・マグナ』の名で知られる書物を著わし，N.タルタリアの発見した3次方程式の解法およびカルダーノの弟子の L.フェラリが発見した4次方程式の解法を公表した。また，初めてゲームにおける確率に関する体系的な著書を発表している。 60年に息子が殺人罪で処刑され，大きなショックを受けた。 70年には異端の罪で投獄され，数ヵ月後に釈放されたが，教授の地位と書物を公表する権利を失った。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

カルダーノ

イタリアの数学者，医師，自然哲学者。諸学に通じた万能人として名声を博したが，とりわけフェロ，タルターリアらと並ぶ三次方程式の解法の発見（1545年）で知られる。確率論の先駆的研究，個性的な《自伝》（死後刊行，1663年）でも有名。
→関連項目タルタリア

出典　株式会社平凡社

世界大百科事典（旧版）内のカルダーノの言及

【永久機関】より

…有名なのはコングリーブWilliam Congreve卿(1772‐1828)の考案で，海綿製のベルトと重量物でつくったベルトを重ねて斜めに二つの滑車に掛け，下半分を水中に置く方式であった。磁気を利用するものとしては，13世紀にP.deマリクール(ペトルス･ペレグリヌス)が永久に針が回転する装置を図に描いているほか，カルダーノが磁気を利用した永久機関の可能性を示唆したことをアントニウス･デ･ファンテスAntonius de Fantesが記しているが，これについてはW.ギルバートが実験ぬきの思いつきにすぎないと批判している。上述のウィルキンズも，斜面に穴をあけ磁石で鋼球を引き上げては落とす装置を考案している。…

【カメラ】より

…
【カメラの歴史】
　すでに述べたようにカメラ･オブスキュラはかなり古くからあり，その原理についてもイブン･アルハイサム(アルハーゼン)，R.ベーコンらは知っていたといわれ，レオナルド･ダ･ビンチもカメラ･オブスキュラの正確な記述を残している。イタリアのG.B.dellaポルタは，1589年の《自然魔術》という著書の中でカメラ･オブスキュラを一般に広く紹介したが，すでにこれより以前にG.カルダーノやバルバロDaniel Barbaro(1528‐70)が両凸レンズを用いて明るい映像を得る方法を述べており，またバルバロは68年の著書の中で鮮明な映像を得る方法として絞りの採用も提案している。当時，カメラ･オブスキュラはもっぱら絵をかくときのトレース用として利用され，その小型化も図られたが，実用的なポータブル化に成功したのはドイツの僧ツァーンJohann Zahn(1641‐1707)であり，1685年の彼の著書を見ると，彼のカメラ･オブスキュラには光路に斜めに反転可能な鏡があって，水平なピントグラス上に映像を結ぶ一眼レフ方式になっていることに驚かされる。…

【電気】より

…しかし，このころには，コハクがちりを引きつけるためには，コハクを摩擦することが必要であるということは十分認識されておらず，また磁石の引力とも明確に区別されていなかった。磁気現象と電気現象との区別を確立したのは，16世紀のイタリア人G.カルダーノである。彼は，磁石が鉄しか引かないのに反して，摩擦されたコハクは軽い物体ならなんでも引きつけること，磁石はいろいろの物を通しても力を及ぼすが，コハクの引力は間に物をおくとさえぎられることなどを観察した。…

【人相学】より

…西欧人相学にはこのように，古くから動物類推と占星術という二つの方法があった。　占星術を好んだ神聖ローマ皇帝フリードリヒ2世の寵を受けたM.スコットの《人相論》，三次方程式の解法で知られるG.カルダーノの《占星術的人相学》，教皇アレクサンデル6世に破門されて焚刑に処せられたG.サボナローラの伯父M.サボナローラが著した《人相学》など，いずれも占星術による人相学である。他方，11世紀のアラビア科学を代表するイブン･シーナーの《動物の諸本性》は，霊魂と動物の形態とを目的論的に説明して神の摂理を説き，これに触発されたアルベルトゥス･マグヌスは《動物について》の中で人相学を論じている。…

【ランプ】より

…　ルネサンス時代に入ると科学思想が発達して，オイル･ランプにも改良が加えられた。その第1段階が，イタリアの数学者にして医者のG.カルダーノの創案したカルダン(カルダーノ)灯であった。これは灯火を明るくして，長時間点火できるように，油壺を灯芯よりも高いところに設置した形式であった。…

※「カルダーノ」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」