視差（読み）シサ

デジタル大辞泉

し‐さ【視差】

１ 目と対象物との相対的位置の移動または差違による、網膜上の結像の位置の変化。対象物に対して、両眼の視線の挟む角度で表される、両眼視差によって対象物の遠近を知覚する。
２ 天文学で、天体の一点を2か所から見たときの方向の差。地球の中心と観測者の位置とを結ぶ線、すなわち半径を基線とする日周視差は太陽系内の天体の距離の測定に、また、地球の公転軌道半径を基線とする年周視差は恒星の距離測定に利用。
３ 写真測量で、ある地点を隣り合う2枚の写真で写したときの方向の違い。その地点までの距離を算出できる。
４ 写真で、ファインダーの視野と実際に写る範囲との違い。

出典　小学館

精選版 日本国語大辞典

し‐さ【視差】

1. 〘 名詞 〙
2. ① 同一の物体を二つの地点から観測した場合の方向の相違。両眼の視差や、移動することによって起こる視差から距離が判断される。
3. ② 天文学で、天体の一点を二つの地点から観測した場合の方向の差。天体までの距離測定に利用される。
   1. [初出の実例]「後測 太陽離地、暗厄里亜里一億二千万里、〈其過差する所、十一分第十二分一に及はずといへり、一億二千万里は我五千万里余なり、是はボイスに見たり、按ずるに、後測は太白視差を察して得たり〉」(出典：暦象新書（1798‐1802）上)
4. ③ カメラで、ファインダーで見た被写体とレンズで撮影した画像とのずれ。パララックス。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

視差
しさ

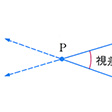
ある天体を2地点から見たときの方向の差。2点A、Bから1点Pを見るときに∠APBを視差という（図A）。視差は、距離APやBPを直接測定できないとき、これらを求めるのに重要な量（数値・計測値で、角の大きさは角度で表す）である。天体の距離を求めるのに、レーダーやレーザーなどで直接に測定できる場合は別にして、視差を測るのがもっとも基本的な方法である。視差は観測点A、Bのとり方などにより、いろいろ考えられる。

［大脇直明］

地心視差

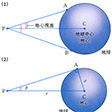
図Bの(1)において、A、Bを地球上の2点とすると、視差は∠APBとなる。このときBのかわりに地球中心Cから見たような視差を計算しておくと便利であり、こうして求めた視差∠APCを地心視差という。また、より便利なものとして、地表で天体を地平線に見たときの地心視差（地平視差）、さらに赤道上の観測者が見た地平視差（赤道地平視差）が用いられる。地心視差は太陽系天体の距離測定に用いられる。すなわち、図Bの(2)において、地心Cと天体Pとの距離をr、観測点Aと地心Cとの距離をaとすると、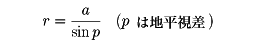

となる。

［大脇直明］

年周視差・三角視差

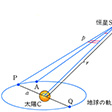
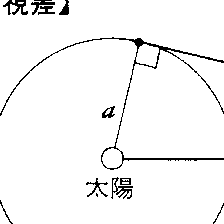
図Cにおいて、太陽Cから見た恒星Sの方向はCS、すなわち天球上の星の位置はC'であるが、公転軌道上の地球Aから見るとSは天球上のA'に位置して見える。このC'とA'のずれ、すなわち∠ASCが視差で、地球の公転運動に伴い1年周期で変化するので年周視差とよばれる。軌道面上でCSに垂直な位置P、Qでは年周視差が極大となる。この極大値を三角視差pという（しばしばこれを年周視差ということがある）。いま、地球・太陽間の平均距離をa、恒星までの距離をrとすると、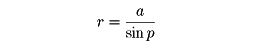

という関係から、pを測ればrが求められる。これが恒星までの距離を求めるもっとも基本的な方法である。しかし現実には恒星はきわめて遠方にあり、三角視差は非常に小さい。したがって、この方法は、近い恒星（三角視差が数十分の1秒角以上）にしか適用できない。なお、1秒は円周（360度）の129万6000分の1の角度で、三角視差が1秒角の距離を1パーセクといい、これは約20万天文単位、約31兆キロメートル、3.26光年に相当する。

［大脇直明］

永年視差

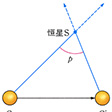
太陽は恒星の間をヘルクレス座の方向に秒速約19.5キロメートルの速度で運動している。したがって、太陽をC、恒星をSとすると（図D）、ある時点には星がCSの方向に見えるが、何年かたつとC'Sの方向に見える。このときの∠C'SCを永年視差という。実際はSも動いているので、これからただちにSの距離は求められないが、多数の星それぞれの特有の運動が平均的にみてゼロと仮定すると、統計的に方向のずれの大小で星の距離を推定することができる。

［大脇直明］

星流視差

星団などのなかには、太陽に対して同じ方向に運動していることが知られているものがある（例、ヒヤデス星団）。これらの星団に属する星Sは太陽Cに対して平行運動をしているので、天球上の1点Kに収束して動いているように見える（図E）。このとき∠SCK、Sの方向の年間変化（すなわちSの固有運動）およびSの太陽に対する視線速度を観測すると、Sまでの距離がわかる。このような距離の求め方を星流視差の方法という。

　なお、以上は幾何学的ないし運動学的方法によって視差（すなわち距離）を求めるもので、視差という本来のことばが用いられているのであるが、ほかの方法、たとえば恒星の明るさからも距離を推定することができる。このような方法で得られた距離に対しても視差ということばを用い、たとえば測光学的視差という場合もある。

［大脇直明］

『ロジャー・B・カルバー著、長谷川俊雄訳『実験天文学ワークブック』（1988・恒星社厚生閣）』▽『斉田博著『天文の計算教室』新装版（1998・地人書館）』▽『長沢工著『日の出・日の入りの計算――天体の出没時刻の求め方』（1999・地人書館）』

[参照項目] | 恒星 | 公転 | 固有運動 | 視位置 | 視線速度 | 太陽視差 | ヒヤデス | 分光視差

視差〔図A〕

地心視差〔図B〕

年周視差・三角視差〔図C〕

永年視差〔図D〕

星流視差〔図E〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

視差 (しさ)
parallax

同一点を異なった2点から眺めたときに見える方向の違い，すなわち，二つの方向の間の角度を視差という。恒星の場合，地球の公転軌道上の位置の違いで視差があらわれるので，年周視差という。また，地球軌道の半長軸を基線尺にして三角測量の方法で恒星までの距離が決定できるのでこれを三角視差ともいう。年周視差による星の動きは，黄経方向にのびた微小楕円で，その星の黄緯をb，視差をpとすると視差楕円の半長軸はp，半短軸はpsinbとなる。したがって黄道上の星は直線上を往復運動し，黄道の極では円運動になる。年周視差pは地球の公転軌道の半長軸a（＝1天文単位）を基線尺にするので，恒星までの距離rは視差の逆数であらわされ，r＝a/pとなる。視差1″の距離を1パーセク（pc）といい，3.26光年に当たる。視差0.″1ならば10パーセク，0.″01ならば100パーセクになる。

　年周視差の決定には長焦点望遠鏡により，同一星野を日をおいて何枚も撮影し，周辺の星に対する動きを決定するのであるが，この場合，年周の楕円運動である視差と，時間に比例して直線運動をする固有運動とを計算によって分離しなければならない。視差観測は現在アメリカ海軍天文台を中心にして行われているが，1988年に打上げ予定の測定衛星〈ヒッパルコス〉により0.″001の精度の観測が期待されている。

　視差の現象は地動説の検証としてG.ガリレイによって予言されたが，当時の観測精度ではこれを検出するには至らず，その後多くの人がこれに挑戦した。J.ブラッドリーはこれをめざして光行差を発見し，F.W.ハーシェルは近接した星対で視差を検出しようとして連星系を発見した。初めて視差の値が発見されたのは1838年ドイツのF.W.ベッセル（はくちょう座61星），南アフリカのケープ天文台のヘンダーソンT.Henderson（ケンタウルス座アルファ星），ロシアのF.G.W.ストルーベ（ベガ星）によるものである。現在知られている中で視差のもっとも大きい恒星はケンタウルス座プロキシマ星で，0.″750である。地上観測で視差決定の限界は0.″01までであり，これ（100パーセク）より遠い星の距離を決定するには，連星系の軌道周期からきめる力学視差，ケファイド変光星の変光周期からきめるケファイド視差，スペクトル型からきめる分光視差など間接的な方法による。太陽系内の天体の場合には地球の自転による視差，すなわち地心視差（日周視差ともいう。その最大値が地平視差である）がきいてくる。太陽までの距離では赤道上では8.″794148になる。これを太陽赤道地平視差という。
執筆者：石田 五郎

図－視差

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

視差【しさ】

同一対象を二つの観測位置から見たときの方向の差。角度で表す。対象までの距離と２観測位置の距離（基線）と視差の間には，三角法で計算できる一定の関係が成り立ち，三角測量・測距儀・距離計等に応用される。天文学では地球の半径を基線とする視差を日周視差または地心視差といい，特に対象天体が地平線にあるとき最大となり地平視差という。太陽系内の天体の距離測定に利用できる。恒星の距離測定には地球の公転軌道半径を基線とする年周視差を用いる。
→関連項目距離計｜ステレオグラム｜分光視差

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

視差
しさ
parallax

1つの天体を異なる2つの場所から見たときの方向の差をいう。相手の天体が恒星の場合は，地球と太陽から見た恒星の方向の差を用いる。これを年周視差といい，その角度 (秒) の逆数が恒星の距離を表わすのに用いられる。相手が太陽，月，惑星などの場合は，地球の中心と観測者から見たこれらの天体の方向の差を用いる。これを地心視差という。実際にその方向差を測定するには，背景のごく遠距離にある恒星の方向を基準とする場合が多い。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の視差の言及

【恒星】より

…このことは恒星が扁平な銀河円盤をなして空間分布している事実の現れである。
［年周視差と固有運動］
　星の位置の測定は明るさと色の測光，スペクトル分光とともにもっとも基本的な天文測定である。無限遠にあると考えてもよいほど遠い恒星を基準とすれば，観測される恒星位置の変動は年周視差と固有運動によるものとである。…

※「視差」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」