翻訳|survey
精選版 日本国語大辞典 「測量」の意味・読み・例文・類語
そく‐りょう‥リャウ【測量】
- 〘 名詞 〙
- ① あれこれと推測して考えること。
- [初出の実例]「仏法之恩。誰得二測量一」(出典:江都督納言願文集(平安後)六)
- 「無常有待之世因果雖レ難二測量一、猶不レ堪二悲哀一耳」(出典:実隆公記‐文明一六年(1484)正月一六日)
- [その他の文献]〔顔氏家訓‐省事〕
- ② 天体や建造物などの高さ、深さ、長さ、広さ、位置、方向、距離などを機器を用いてはかること。
- [初出の実例]「此度の月食は、東西両地共、初・甚・復測量出来、近来珍敷儀」(出典:間重富宛高橋至時書簡‐寛政一〇年(1798)一一月二日)
- ③ 地球表面上の形状を測定すること。種々の機械を使って、地表の高低、深浅、位置、方向、角度、距離などをはかり、図示すること。
- [初出の実例]「是月命二伊能忠敬一、測二量豆相常総及陸奥沿海一」(出典:日本財政経済史料‐二・経済・検地・全国測量・享和元年(1801)三月日)
- 「其沿海(かいがん)を測量(ソクリャウ)せんとて水師提督ロッシルスをして」(出典:新聞雑誌‐一号・明治四年(1871)五月)
- [その他の文献]〔国朝漢学師承記‐銭大昕〕
日本大百科全書(ニッポニカ) 「測量」の意味・わかりやすい解説
測量
そくりょう
survey
地球上にある自然または人工の各物体の相互の位置関係を測定して求め、これを数値や図面で表す技術の体系。数値とは多くの場合、ある決められた座標系での座標値であるし、図面とは各種の地図である。また宇宙探査技術の進歩により、測量の対象はかならずしも地球上の物体に限らず、たとえば月の表面など、他の天体での測定も行われるようになった。
[中村英夫]
測量の歴史
測量の歴史は人類が定住し農耕を営むようになったときに始まるといってよい。農業用水や排水を適切に流したり、耕地の境界を決めたりするには、土地を測るなんらかの技術が必要だからである。学問的興味が高まったギリシア時代には地球球体説が唱えられ、紀元前200年にはエラトステネスにより、エジプトのシエナとアレクサンドリアの間の位置関係を、今日でいう多角測量に近い方法により求め、これより地球の一象限の弧長を1万1560キロメートルであると計算した。中世ヨーロッパでは科学的なものの見方は消え去り、怪しげな地図が描かれるようになった。しかし、イスラム世界では11世紀に磁石により方位を測定する羅針盤が発明され、これを利用して航海するための海図がつくられ、これがのちに15世紀に入ってのスペイン等による大航海時代を生むこととなる。
近代的な測量技術が生まれるのはもちろんルネサンス以降である。16世紀末のメルカトルによる円筒図法の発明は、球体の地球を地図として平面上に描くことを可能にした。17世紀初頭(1617)には、オランダのW・スネル(ラテン語読みでスネリウス)により三角測量法が発明された。17世紀中期にフランスで発明される望遠鏡とバーニア目盛りのついた測角器を用いることにより、長い距離を巻尺で精度よく測るという困難な作業を減らし、かわりに多くの角を測定して、広い区域にわたって高い精度で位置の測量をすることが可能となった。
測量につきものの大量の計算は、当時の人々にとってはもっとも労多く困難な作業の一つであった。17世紀にはスコットランドのJ・ネーピアが対数を発明し、さらにブリッグズが対数表を作成した。これにより乗除算を加減算に置き換えることができるようになった。19世紀初頭には、ドイツのガウスにより誤差理論が確立され、測定に含まれる誤差を合理的に処理し、測定の信頼性を高めることを可能にした。
18世紀には、ルイ15世が測量家カッシーニにフランス全土の測量への着手を命じ、約100年後の1818年にカッシーニ図とよばれる縮尺8万6400分の1の地形図が完成した。
18世紀には日本にもオランダを通じてヨーロッパ流の測量法が導入され、これと日本古来の方法が結び付いて多くの測量がなされた。たとえば1727年(享保12)福田履軒(りけん)は富士山の高さを測定し、3885.96メートルという値を得ている。特記すべきは伊能忠敬(いのうただたか)による全国の海岸線の測量で、道線法とよばれた多角測量により、1800年(寛政12)から18年の歳月をかけて、今日の水準からみてもきわめて高い精度で日本の国土の形状を示す地図を作成した。
19世紀以降、欧米や日本をはじめとして近代的地図の作成が進展し、これを支える三角点や水準点などの基準点網が整編された。また鉄道、道路、ダムなど大土木工事のための精密な土木測量も発展した。
20世紀に入っての一つの大きな発展は写真測量の導入である。その能率の高さのため、これは第二次世界大戦後とくに普及し、今日では地図づくりの大半が空中写真測量によっている。電子計算機の普及は、測量計算の労を劇的に減らし、また厳密な計算を可能ならしめたことにより、その影響は計り知れないほど大きい。20世紀末から電波星の電波を使った超長基線電波干渉計(VLBI)、人工衛星を使ったSLR(Satellite Laser Ranging人工衛星レーザ測距)、全地球測位システム(GPS)などの宇宙測地技術による国際共同観測が活発に行われ、地球規模の高精度な国際地球基準座標系が構築されるようになった。21世紀になって、地理空間情報システムを支える基盤技術として測位衛星システムGlobal Navigation Satellite System(GNSS)の開発が世界的に進められ、アメリカのGPS以外にもロシアのグロナス、EUのガリレオ、中国のコンパスなどが登場した。これらにより、測量の効率化および土木における情報化施工などへの幅広い利用が期待されている。また電磁波による距離測定の発明は、測量方法を大きく変えた。人工衛星からのリモート・センシングは、地表の映像を広範囲にわたって即座に得ることを可能にし、小縮尺の地図づくりや資源調査などに広く利用されつつある。
[中村英夫]
測量の基準
地上の地物(自然または人工の物体)の位置を求め、これを表現する場合、まず問題となるのはその位置の基準を何にとるかである。たとえば地点の高さを表す場合、その高さとはどこからの高さをさすかである。高さを表すもっともわかりやすく実用的なのは、海面からの高さである。海面の高さと一概にいっても、これは波や潮汐(ちょうせき)などにより時々刻々変化しているので、実際はある位置で長い年月にわたって測定した海面の高さの平均値を求めて、高さの原点すなわち0メートルとしている。日本の大部分では、東京湾の霊岸島で測定された平均海面高を0メートルとして高さが決められている。これを標高とよんでいる。
球状、正しくは極の方向の直径が赤道の直径より約0.3%短い回転楕円(だえん)体である地球上での位置をもっとも無理なく表す方法は、緯度、経度と標高を用いて表現する方法である。日本では、地球重心を中心とするGRS80(Geodetic Reference System 1980)楕円体が測量の基準として用いられている。たとえば東京の三宅坂(みやけざか)にある水準原点は、北緯35度40分38秒、東経139度44分52秒、高さ24.3900メートルと表される。しかし、この緯度、経度のような球面座標で表すのはきわめて繁雑であるし、わかりにくく実用的ではない。そこで、地球の表面を多数の平面からなる多面体で近似し、一つの平面内では平面直角座標系で表現する方法が広く採用されている。一つの平面の大きさをどの範囲までとるかは、地球の表面をどの程度の精度で近似するかによって決まる。日本で用いられている平面直角座標系では、地球面上で測った弧長である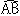 と、それに近似した平面上で測った長さ
と、それに近似した平面上で測った長さ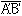 との差が1万分の1以内となるようにしている()。このような近似精度を保つようにすると、一つの座標系のカバーする範囲は約260キロメートル四方となり、日本は、に示されるように、19の座標系で覆われることになる。この座標系では北の方向にX軸が、東の方向にY軸がとられ、地点の平面位置はこのX、Yで表され、これと標高Zですべての地点の三次元的な位置は表されることになる。また、GNSS測量などでは、測量の基準として地心直交座標系が用いられている。この座標系は、地球の重心を座標原点とし、赤道面内でグリニジ子午線との交点方向にX軸、東経90度方向にY軸をとり、自転軸をZ軸とする直交座標系である。
との差が1万分の1以内となるようにしている()。このような近似精度を保つようにすると、一つの座標系のカバーする範囲は約260キロメートル四方となり、日本は、に示されるように、19の座標系で覆われることになる。この座標系では北の方向にX軸が、東の方向にY軸がとられ、地点の平面位置はこのX、Yで表され、これと標高Zですべての地点の三次元的な位置は表されることになる。また、GNSS測量などでは、測量の基準として地心直交座標系が用いられている。この座標系は、地球の重心を座標原点とし、赤道面内でグリニジ子午線との交点方向にX軸、東経90度方向にY軸をとり、自転軸をZ軸とする直交座標系である。
[中村英夫]
測量の分類
測量と一概にいっても、その段階や目的、測定方法によっていくつかのものに分けられる。
測量段階では、基準点測量と細部測量とに大別される。基準点測量は骨組測量ともよばれ、三角点、多角点、水準点などの基準点を設け、その地域全体に適当に分布させて座標を正確に測定する測量である。これらの点は、その周辺についての種々な測量を行うに際して基準となるものである。日本では国土地理院によりこれらの基準点が国土全域にわたり多数設けられており、多くの場合これらの既設の基準点の測量成果を利用できる。たとえば三角点は、一等三角点が1600平方キロメートルに1点、すなわち約45キロメートル間隔に設けられ、以下二等・三等・四等三角点(四等三角点は2平方キロメートルに1点、平均間隔で1.6キロメートルの割合)がより密に設けられている。また高さを示す水準点は、一等水準点が国道や主要地方道沿いに約2キロメートル間隔に、二等水準点が1キロメートル間隔に設けられている。国で設置されたこれらの基準点は、定期的に測量され、地殻変動などの測定などにも役だっている。
細部測量は比較的狭い区域をある目的のために詳細に測定する測量である。たとえば、与えられた基準点を用いてその周辺区域にある地物の位置を測定して平面図をつくったり、それにさらに地形の高さを測量し、等高線で地形を表現し地形図を作成したりするのがこれである。
測量は種々の目的のために行われるが、その目的により測量内容はさまざまである。これらを総称して応用測量とよぶこともある。もっとも広く行われる応用測量は地形図をつくる地形測量である。そのほか鉄道、道路などを設計し、これを建設するために行う路線測量、土地の所有境界を決定し、これを地籍図として描き、また土地面積を測る地籍測量、河川の断面形状や流量を測る河川測量、海の海底地形を測量する海洋測量など種々の応用測量がある。
[中村英夫]
測量における基本的測定
測量において通常用いられる基本的な測定は、対象となる地点間の距離、角、高低差の測定である。これらの測定を組み合わせて多角測量、水準測量など種々の測量方法が行われる。
距離測定は二つの地点間の水平距離を求めようとするものである。ガラス繊維や鋼などでできた巻尺や、高い精度の測定を行う場合にはインバール尺(鋼とニッケルの合金でできた、温度による伸縮の小さい巻尺)を用いる。1970年代には、電磁波測距儀とよばれる器械を用い、光波を2点間を往復させてその位相差により距離を瞬時に求める方法が使われるようになった。長い距離を10万分の1から100万分の1というような高精度で測定することは、地形の起伏などもあり、従来はたいへんむずかしいものであったが、電磁波による距離測定の普及により、距離の測定は非常に正確かつ効率的に行われるようになった。
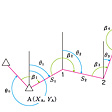
角測定は、ある地点Pから他の1点Aを見た方向PAと、もう一つの他の1点Bを見た方向PBのなす角を測定するものであるが、にみるように、水平方向の角α(水平角という)を測定する場合と、鉛直方向の角β(鉛直角という)を測定する場合がある。これらの角の測定には、角度目盛りがつけられた分度器のような目盛盤と、その目盛盤の中心に回転軸をもつ望遠鏡からなるトランシット(セオドライト)が用いられる。1990年代以降、電磁波測距機能と電子的角度測定機能を一体化したトータルステーションが普及している。内蔵のコンピュータにより水平距離、鉛直距離および座標値の計算、観測値の記録、自動視準、通信などの機能があり、測量の自動化と飛躍的な効率化に貢献している。
高低差の測定はレベルとよばれる光学器械を用いて行われる。これは、地球の重力方向すなわち鉛直方向に直角な面の上に望遠鏡の見通し線がくるように調整できる水準装置付きの望遠鏡である。このレベルにより、測定すべき2地点間に立てた標尺の値を読み、その読定値の差として高低差が求められる()。山の高さなど、高低差の大きい2点間を測る場合には、この標尺とレベルを次々と置き換えて測定する。また山の高さや樹高hなどを比較的低い精度で測るときは、セオドライトにより鉛直角θを測定し、それと測定すべき地点と器械の位置との間の距離lを測りh=ltanθとして求めることもある。
GNSS測量は地球を周回する複数の測位衛星の電波を受信して2点間の相対位置ベクトルを求める測量である。位置が精度よく与えられている測位衛星から送信される電波を地上の2点で受信し、その位相差を測定することにより、2点間の相対的な位置ベクトルが地心直交座標系に基づいて決定される。新点の地心直交座標は、計算により経緯度および楕円体高に変換することができる。楕円体高は、楕円体表面から測定した高さで、海面上の高さ(標高)とは異なる。日本ではジオイド高(楕円体高-標高)の分布が詳しく調べられているため、楕円体高を精度よく標高に変換することができる。
多くの測量、とくに基準点などの点の測量は、この距離、角、高低差という三つの基本的測定の組合せによって行われるが、写真測量はこの三つの測定とは非常に異なった測定方法を用いる。写真測量は、地上または空中の異なる2点から撮影された同一対象物または地区の写真を用いて平面位置(X、Y)と高さZを一挙に測定し、座標値を求めたり地図を描いたりするものである。写真は中心投影されたものであり、たとえば上空から撮影された写真では、高い塔や建物はのように写真上では横に倒れたような形に写るため、高さの情報が写真に含まれることになる。これを利用して2枚の写真を立体的に観測して各点の正確な高さを、平面位置とともに写真測量図化機とよばれる装置などを使って求め、また正射投影に変換して地図として描くものである。
[中村英夫]
測量の方法
測量をして点の位置を求めたり、それを地図として表すには、一般に次の方法が用いられる。すなわち、点の測量には、三角測量、多角測量、水準測量、あるいはこれらを組み合わせた測量法が、また細部の面の測量には平板測量が使われる。また写真測量は点および面を一挙に求める方法でもある。
三角測量の原理は、三角形の一辺と二つの角を測定し、これより三角法の正弦法則を用いて他の辺長を求め、これより三角形の頂点たる各点の座標を求めるものである。のように三角形を順次つないでゆくことにより、一つの辺長を測るだけで、あとは角のみを測定して、広い区域にわたり各点の座標を決めることができる。
多角測量は、トータルステーションを用いる手法とGNSSを用いる手法がある。トータルステーションを用いる場合には、のように各点を結ぶ折れ線について、その辺長を測定すると同時に夾角(きょうかく)を測定し、北からの角、いわゆる方向角を求め、これより各点の座標を計算して決めるものである。
GNSSを用いる場合には、各折れ線は位置ベクトルとして求められるので、各点の座標は、これらの位置ベクトルの和として計算される。
水準測量はの高低差測定を行って水準点の標高を求めるものである。
平板測量は、座標など位置の確定している点(図根点とよばれる)の直上に平板とよばれる紙を貼(は)った板を水平に置き、この上で、地図上に描くべき地物の位置とその方向線を紙の上に描き、同時にそこまでの距離を測って描き、地図を作成する方法である。
地形図をつくる測量のほとんどは航空機により撮影した写真による空中写真測量によっているが、狭い範囲の地形などを測量する場合には電子平板による測量が用いられる。上記の応用測量はこれらの測量方法を目的に応じ組み合わせて行われる。
[中村英夫]
『武田通治著『測量――古代から現代まで』(1979・古今書院)』▽『日本測量協会編・刊『現代測量学1~7』(1981~1988)』▽『檀原毅他編『測量叢書』全5巻(1987~1989・日本測量協会)』▽『吉澤孝和著『図解 測量学要論』(2005・日本測量協会)』▽『石井一郎編著『最新測量学』第2版(2005・森北出版)』▽『日本測量協会編・刊『測量学事典』(2007)』▽『測量用語辞典編集委員会編『測量用語辞典』(2011・東洋書店)』
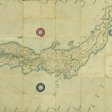
『日本図』

江戸時代の測量風景

日本水準原点標庫
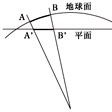
球面上と平面上の距離〔図A〕
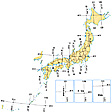
平面直角座標系〔図B〕
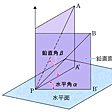
水平角と鉛直角〔図C〕
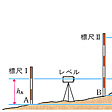
高低差の測定〔図D〕
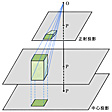
中心投影と正射投影〔図E〕
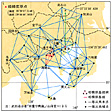
相模原基線網と一等三角網ならびに経緯度…
多角測量の一例〔図G〕
改訂新版 世界大百科事典 「測量」の意味・わかりやすい解説
測量 (そくりょう)
survey
測量とは,互いに位置の異なる点の間の相対的位置関係を求めるものであるが,さらにこれら各点の位置関係やその他の資料を基礎として地図等を作成したり,土地の面積や体積等を求めるものもいう。また天文観測により地球上の観測点の天文学的な緯度,経度を求めるもの,あるいは地磁気,重力等を対象とした地球物理的な測定,河川の流速,流量等の測定,設計図上の点を地上に設定することなども測量の範囲に含めることが多い。
測量の歴史
西洋
測量の起源はエジプト王朝時代にさかのぼって求められる。当時のエジプト人にとってナイル川は生活の糧の源泉であったが,毎年おきる洪水は耕地等の土地の境界を破壊するものであった。この結果を原形に復するための境界の設定が必要となり,このための技術として測量技術が発達したものと考えられている。エジプト時代の測量機器,方法については簡単な測量縄,測量幹の使用以外に詳細は不明であるが,ギーザのピラミッド(前2500ころ)の建築技術,その基礎の方向から,測量の精度はかなり良いものであったことがうかがわれる。
ギリシア時代には学問の進歩に伴い測量の分野でも発展がみられ,メトンMetōnによる方位の測定,エラトステネスによる地球外周長の測定があり,またヘロンによる経緯儀と水準器を組み合わせた測量器と考えられるディオプトラや歯車式の距離計についての記述,プトレマイオスによる天文観測用の象限儀(四分儀)についての記述が残っている。ローマ時代の測量手段はこれ以前のものと大きな差は見られないが,測量機器,方法の中部ヨーロッパへの普及が著しい。ローマ時代には道路網の整備や地籍調査が国家的に実施されているが,そのために重要な役割を果たしたのはグロマgromaとよばれる直角器の一種である。グロマは木の棒2本を互いに直交させ,その四つの腕の先からおもりをつけた紐をたらしたもので,その紐を使って照準を合わせることで角度を直角に合わせることができた。当時の土地の単位は矩形であったと考えられ,グロマと測量幹が当時の主測量器であった。中世時代の科学はおもにアラブ人により保持,向上させられていたが,測量部門では中世後期に至るまで若干の改良はあったにしても,一般にはこの時代以前のものが広く用いられていた。
ルネサンスとともに測量技術にも大きな進歩があった。レオナルド・ダ・ビンチは距離測定車のデザインを描いており,またJ.F.フェルネルは1525年に測距車により長距離の測定を行い,弧長測量を実施している。この時代には地理学的発展,航海術の進歩に伴い,地図や測量データへの要求が一段と強まった。1530年ころにはオランダで現在の巻尺の元となった測量鎖が初めて用いられ,1600年ころには水平角測定装置が開発され,このような装置に初めてセオドライトtheodoliteの名称が記されている。平板測量器具はヘンマ・フリシウスRegnier Gemma Frisius(1508-55)により発明されたといわれ,それがプレトリウスJohann Praetorius(1537-1616)により広められた。
17世紀に入ると多くの主要測量器が開発されている。すなわち,G.ガリレイやJ.ケプラーらによる望遠鏡の開発,テベノMelchisédech Thevenot(1620-92)による気泡管の発明などがある。また1617年にはオランダのスネルWillebrod van Roijen Snell(Snellius。1591-1626)により近代的な三角測量方式が実用化されるなど,測量方法にも進歩が見られる。18世紀になるとフランスでは土地測量による地籍の確定に関する法律が議会を通過し,これには三角測量法を用いると明記されるなど,測量の精度の向上が図られ信頼されるに至った。1795年にはC.F.ガウスが,ほとんど同時にA.M.ルジャンドルが,最小二乗法理論を発展させ測量データの精度を一層向上させた。この時代にはほぼすべての地上測量用器の基本は開発され,以後その改良が進められていたが,20世紀後半における電子工学の発展に伴い電磁波測距儀が開発され距離測量が広く用いられるようになったことと,写真技術の発達に伴う写真測量の発展に著しいものがある。さらに,人工衛星や電波星を利用した測量が開発されるに及び,測量手段は宇宙にまで発展している。
日本
日本における測量については,遺跡等から古墳時代にさかのぼるといわれている。大化改新(645)の際には土地制度として班田収授法が定められたが,土地の測量が重要な要素となっている。710年(和銅3)唐の長安にならって大和の北部に平城京が築かれた。平城京は南北約4.8km,東西約4.2kmの長方形で,市街は碁盤目状に道路で区切られており,中国大陸の文化とともにかなり進んだ測量技術が輸入されたものと考えられる。その後794年(延暦13)山背(やましろ)に平安京が築かれたが,これは平城京よりもさらに規模の大きなものであった。その後は江戸時代まで,奈良時代に作られた〈行基図(ぎようきず)〉が残されていたことから推測されるように,著しい測量技術,地図作成技術の進歩はなかった。
江戸時代に入ると西欧式の測量器具や方法が伝えられたが,初期には鎖国の影響もあり,特記すべきものもなかった。中期に入り蘭学の発達が理学,医学等に及んだが,測量の分野でも特記すべき進歩があった。それは伊能忠敬による日本全国の海岸線に沿った測量,地図作成である。忠敬は1800年(寛政12),56歳の老軀にもかかわらず蝦夷(えぞ)地の測量にまず着手して以後,実に18年の星霜を経て日本国土の実体を明らかにした。この測量の結果を日本全図としてまとめる途中,忠敬は1818年(文政1)に死亡したが,その仕事は幕府天文方の高橋景保により引きつがれ,1821年に《大日本沿海実測全図》(大図214枚,中図8枚,小図3枚)として完成した。これらを〈伊能図〉ともいう。忠敬の使用した主要な測量器具は折衷尺,間縄,方位盤,象限儀,羅鍼(らしん),量程車等であるが,測量結果の正確さは当時日本のみならずシーボルトら外国人にも高く評価された。幕府は1831年(天保2)全国の大名に国郡の境界,市邑,面積等を調査させ,自領の国図を作らせているが,これは38年に《天保国絵図》として完成した。〈伊能図〉は内陸各地の状況は必ずしも詳しくなかったので,この絵図はその地方版としての役割と考えられた。明治になり陸軍陸地測量部はこの2種の図を基礎として《輯製20万分1図》を作成し広く利用した。忠敬以後,武田簡吾は《輿地(よち)航海図》を作成し,また勝海舟が《大日本沿海略図》を,佐藤政養が《大日本精図》を編集している。
明治に入ると兵部省,工部省等がおのおのの目的で近代的測量を開始したが,1878年陸軍参謀本部が設置され,ここに測量課,地図課が編成され,これより全国土を対象とした近代的な全国測量が始まった。この結果は大正末期になり日本全土の5万分の1図として集成され,長期にわたり国民に利用された。なお,測量課,地図課は,1888年陸軍陸地測量部となり参謀本部から分離,第2次大戦後は地理調査所(1960年より国土地理院)に引きつがれている。
測量の基本量と測量機器
2点以上の間の相対位置を求めるには,一般にこれらの点が共通に含まれる座標系を設定し,点間の座標差を測定する。2点が平面上であれば最少二つの測定量が,空間にあれば少なくとも三つの測定量が一般に必要である。この測定量として,角度と長さの二つの基本量がある。
角度
角度の測定は比較的容易であることから,望遠鏡の発明以来,数学の発展とあいまって現在に至るまで広く用いられている。角度測定器として一般に用いられているものは経緯儀である。経緯儀は重力またはこれに垂直の方向を基準として整準し,この状態で付属望遠鏡を2点以上の目標に向け,その間の水平角を,また各点の鉛直角(高度角)を目盛盤上で読みとるものである。日本工業規格(JIS)では,目盛盤をバーニヤまたは指標で読みとるものをトランシットtransitといい,光学的な拡大装置を用いて読みとるものをセオドライトといって区別している。経緯儀の構造は,望遠鏡,水平軸,鉛直軸,鉛直目盛盤,気泡管等から構成される,鉛直軸に直角についている上板から上の上部機構と,鉛直軸,水平目盛盤,整準・求心装置等の下部機構から成り立っている。経緯儀には鉛直軸の構造により単軸型と複軸型がある。単軸型は,鉛直軸が直接に整準台に支持されているため鉛直軸の機械的な精度が高いが,目盛盤と鉛直軸を一体として回転できないので,任意目盛から測角を始めたり倍角法による測角を行うことができない。前者はおもに基準点測量などの精密測量用に,後者は土木測量のような比較的精度の低いものなどに用いられる。
トランシットの分類としては,水平目盛の最小読取値およびバーニヤの個数によりA,B,Cのクラスが,またセオドライトについては最小読取値によりA,B,C,Dのクラス分けがJISで決められている。国土地理院では国の行う基準点測量用として,性能別に特級,1級,2級の分類をしている。現在,角度の数秒までを電子的に読み取りディジタル表示をしたり,電気信号として他に利用できる電子トランシットが開発されている。
長さ
距離測定は三角測量などの角測定に長さを与えるものとして重要な量であり,角度測定よりも古い歴史をもつものであるが,経緯儀の改良などに伴い角測定の精度が高まるにつれ,一部の例外を除き精密測量には用いられなかった。すなわち,比較的精度の低い工事用測量,地籍測量などには鋼巻尺等の尺物が広く用いられていたが,国家基準点のように高い精度の位置が必要な場合には角測量による三角測量方式が採用されてきた。しかし,1940-50年代における電子工学の発達に伴う電磁波測距儀の開発は距離測量の分野に大変革をもたらし,その測定の容易さ,正確さから,三辺測量やトラバース測量が従来の三角測量にとってかわるようにもなった。
距離測量用として一般に普及しているものは繊維製ならびに鋼製巻尺である。繊維製には,細い針金を織り込んだ麻布製,麻と綿,またはガラス繊維と化学繊維を交織し目盛を施したものがある。これらは軽量,折れ曲がりがない,取扱いが容易であるという利点はあるが,湿度の影響を受けやすく伸び縮みがあり,精度の高い測量には適しない。鋼製巻尺は繊維製に比し精度も高く耐久性に富んでおり,建設工事用など比較的精度の高いものに用いられているが,温度や引張力に敏感に反応するため,使用の際に注意が必要である。巻尺の正確さを確保するため,繊維製巻尺については計量法で検定が義務づけられており,鋼巻尺については検量法で検定公差が,JISで種類,形状,寸法などが決められている。精密用巻尺としては線膨張係数の小さいインバール製巻尺がある。これは大規模な三角測量網に長さの単位を与えるための基線測量などに用いられる。
光学的に距離を求めるものとしてタキオメトリーtacheometryの方法がある。測量用としては経緯儀と物尺を一対として用いるものが多い。すなわち測定長の一端に経緯儀を,他端に物尺を設置し,経緯儀により物尺の2点を見た角とスケール長から距離を求めるものである。この方式は精度も低く測量用としてはあまり使われていない。
現在測量用として広く普及しているものはエレクトロニクスを利用した電磁波測距儀である。これには光を用いる光波測距儀と電波を用いる電波測距儀がある。光波測距儀は精度は高いが,長距離測定の場合には天候状況に左右されやすい。一方,電波測距儀は天候の影響は少ないが精度が低い。光波測距儀の原理は,光を強度変調して目標点に設置した反射鏡に向けて発射し,ふたたび測距儀に戻るまでの変調位相の遅れから距離を求めるものである。短距離型には発光ダイオードを,長距離型にはHe-Neガスレーザーが光源に用いられている。
比高または高さの精密な測量には,ふつう水準儀と正確な目盛を持った標尺が用いられる。この測量を水準測量という。
新しい方法では,人工衛星の発射する電波のドップラー効果を利用して観測位置を得るものや,電波星からの電波を2点で受信することにより2点間の距離,方向を求めるものがある。さらに新たに開発されているものに慣性測量方式がある。この原理は,移動物体の加速度を求め,2回積分することにより距離を求めるものである。実際には3軸直交したジャイロと3対の加速度計を用いることにより,三次元量を容易に求めるものである。
測量の分類
測量の分類には各種の方法がある。すなわち,測量範囲の大きさによるもの,測量方法によるもの,測量目的によるもの,測量機器によるもの,〈測量法〉(1949)によるものである。
地球は回転楕円体に近いものであるが,測量の範囲が狭い場合には地表を平面として取り扱うことができる。このような測量を平面測量plane surveyといい,地表を曲率を考えた面として取り扱うものを測地測量geodetic surveyという。前者を小地測量,後者を大地測量ということもある。
測量の方法による分類はかなり広く用いられる。そのおもなものは次のとおりである。
(1)三角測量triangulation 経緯儀による三角形の頂点の角を測量するもので,広域から細部に至る測量に用いられる。日本の骨格を決めるための1,2,3等三角点の位置は,明治以来昭和40年代に至るまでこの方式によっている。
(2)距離測量distance measurement 各種巻尺や電磁波測距儀を用いる直接距離測量と,光学的手段によるタキオメトリーの間接的距離測量がある。簡単な測量から地殻変動用精密測量に至るまで広い範囲で用いられている。特に,精度が良く軽量小型で操作の容易な光波測距儀が開発されて以来,従来からの三角測量方式に代わりトラバース方式が広く採用されるようになった。また1等三角点の位置を決定するような精密な測量には,三辺測量が三角測量に代わり採用されるようになった。
(3)三辺測量trilatelation 基準点により構成される三角形の辺長を直接測定するものであり,辺長が長いほど三角測量より精度の高い結果が得られる。
(4)基線測量base line measurement 三角測量に対して長さの単位を与えるものであり,精密距離測量である。古くはインバール製尺が用いられたが,現在ではこの測量はほとんど用いられない。
(5)トラバース測量traverse survey 角と距離を測定して位置を求める最も簡単な測量方法であり,細部測量に広く用いられる。電磁波測距儀の普及にしたがい広く用いられるようになった。
(6)水準測量leveling survey 水準儀と標尺を用いて高低差(比高)を測定する最も精度の高い方法である。高さの測定にはこのほかに,経緯儀を用いる三角水準測量trigonometric levelingや,気圧計を用いる気圧測高barometric levelingがある。
(7)平板測量plane table survey 平板,アリダードを主要器具として現地において地形図等を作成するものである。大縮尺の図を作成する細部の測量に広く用いられる。
(8)衛星測量satellite survey 人工衛星を用いて地上観測点の位置を求める方法で,星を背景として人工衛星の方向を求める写真観測法,人工衛星までの距離をレーザー光等で直接測定する方法,衛星の発射する電波のドップラー効果による方法がある。電波を用いる方法は現在各国で用いられており,特に密林地など互いに見通しのない地点の測量や,大洋上の船位の確定に利用されている(宇宙測地)。
(9)写真測量photogrammetry 空中写真や,地上写真の撮影,図化などをいう。地形図作成のみならず広い利用範囲をもっている。
測量をその目的に応じて分類するものとして次のようなものがある。
(1)基準点測量control survey 各種測量の基準となる点を設置する測量をいう。三角点や水準点の設置のための測量がその例である。
(2)土地測量land survey 土地面積や境界の測量・図化や,計画にしたがった土地の細分,統合などをいう。
(3)地籍測量cadastral survey 人にはおのおの戸籍が存在するように,土地にもおのおの地籍がある。さらに,土地には所有者,地目などが付随するものであり,土地の境界(面積),所有者,所在地番,地目を求める測量を地籍測量という。地籍の結果は課税の対象となるものであり,すでに前2300年ころのエジプトにその記録があったといわれ,ローマ時代にも国家事業として地籍測量が実施されている。イギリスにおいても1085年にウィリアム1世による土地所有者,範囲,価値を記したドゥームズデー土地台帳が作成されており,スウェーデンでは1692-1702年間にポメラニア地域の地籍測量が平板を用いて行われた。フランスでは1791年に土地測量による地籍の確定法が議会を通過し,土地の境界は三角測量方式に基づくことが明記された。日本における地籍調査はそれぞれの時代の政策や制度と関連して行われている。7世紀後半から形成された中央集権的律令国家では,班田制を施行するための田図を作成している。班田制が崩壊して荘園が発生した中世では荘園領主,守護等が検注と呼ばれる田畑の調査を行っている。この結果作成された台帳を〈検注帳〉という。鎌倉時代には公田の調査が国ごとに行われ,作成された台帳は〈大田文(おおたぶみ)〉といわれる。戦国時代には各戦国大名が検地を行っているが,豊臣秀吉による検地が有名である。これは1582年(天正10)から98年(慶長3)にかけて全国にわたって行われたもので,太閤検地として有名である。江戸時代にも全国の幕領について検地が行われており,検地帳には1筆ごとの地名,地目,面積,耕作者名などが記載されている。明治に入ると近代国家建設の基礎となる財政を確立するため地籍調査を実施し,1筆ごとの字,番号,地目,段別,所有者名を確認している。1931年には国土調査法が制定され,以後近代的な地籍調査が進められている。
(4)地形測量topographic survey 地形図を作成する測量を総称していう。地形図とは,地表面の起伏と地上の人工物,自然物をできるだけ完全に紙面上に縮尺表現したものであり,測量結果をそのまま表現したものといえる。したがってこのような内容の地形図は,各種の編集図や,土地利用図のような主題図などの基礎図として多目的に利用されている。地形測量の方法としては平板測量方式と写真測量方式がある。写真測量方式は広域を対象とし,縮尺が小さいほど有利であるが,使用機器は高価である。一方,平板測量方式は小域に適し,単価が安く,使用器具も安価である。
(5)路線測量route survey 道路,鉄道等の通路のほか,運河,用排水路,架空送電線等の線状構造物建設に必要な測量を総称していう。
(6)河川測量river survey 河川についての計画,維持管理などに必要な資料を得るための測量の総称で,地形測量,水位・水量観測,深浅測量,縦横断測量などから成り立っている。
以上のほか,各目的に応じてトンネル測量,港湾測量,水路測量,市街地測量など多くの測量がある。
さらに,法律による分類がある。これは〈測量法〉による分類で次の三つがある。(1)基本測量 すべての測量の基礎となる測量で,国土地理院が実施するものをいう。(2)公共測量 基本測量以外の測量のうちで,道路,建物のためなどの局地的測量または高度の精度を必要としない測量を除き,測量に要する費用の全部もしくは一部を国または公共団体が負担,または補助して実施するものをいう。(3)その他の測量 基本測量,公共測量以外の測量をいう。
測量の分類にはここにあげた以外に,使用する機器により分類されるものもあった。すなわちトランシット測量,コンパス測量などであるが,現在ではあまり用いられていない。
執筆者:須田 教明
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
普及版 字通 「測量」の読み・字形・画数・意味
【測量】そくりよう(りやう)
 〕京師に在りて、同年の長洲
〕京師に在りて、同年の長洲 寅亮、
寅亮、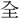 椒の
椒の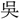
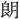 と九
と九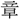 算學、
算學、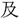 び歐羅巴(ヨーロッパ)の測量・
び歐羅巴(ヨーロッパ)の測量・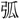 三角の
三角の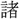 法を
法を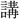
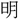 す。
す。字通「測」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
ブリタニカ国際大百科事典 小項目事典 「測量」の意味・わかりやすい解説
測量
そくりょう
surveying
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「測量」の意味・わかりやすい解説
測量【そくりょう】
→関連項目地図|トラバース測量
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の測量の言及
【測量法】より
…国・公共団体が費用の全部または一部を負担ないし補助して実施する土地の測量またはこれらの測量の結果を利用する土地の測量について,その実施の基準および実施に必要な権能を定めるとともに,測量業を営む者の登録の実施,業務の規制を行う法律(1949公布)。陸地測量標条例(1890公布)に代えて制定された。…
※「測量」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

