精選版 日本国語大辞典 「三角測量」の意味・読み・例文・類語
さんかく‐そくりょう‥ソクリャウ【三角測量】
改訂新版 世界大百科事典 「三角測量」の意味・わかりやすい解説
三角測量 (さんかくそくりょう)
triangulation
地上に配置された複数の三角点を線分で結んで形成される網(三角網)において,各線分間の角(水平角)を測定して三角点の水平位置(経度,緯度)を求める測量。地球上での三角点の位置は,旧来経度,緯度,高さの3量によりあらわされるのが普通である。高さが三角点の垂直方向の位置情報を与えるのに対して,経度と緯度は水平方向の位置を与える。三角測量はおもにこの水平位置を決定するための測量の一手法である。ある地区の三角点の位置を決める場合,まず,隣接する三角点を線分で結び三角網を形成する。この網の構成要素は単三角形である。三角点は,これらの三角形のおのおのが極力正三角形に近くなるよう配置される。三角測量では,各三角形の内角すべてが経緯儀(トランシット)と呼ばれる水平角測定機器により測定される。すべての三角形について内角が求められると,三角網の形が決定されたことになる。ただし,この段階では三角網の大きさ,三角網の向きおよび地球上での三角網の位置は知ることができない。すなわち三角網は地球上に固定されておらず,三角点の位置はわからない。このためまったく新しく三角網を設定する場合には,三角測量は単独で行われるわけではなく,三角網を固定するために必要な情報を求める測量も併せて行われる。最小限必要なものとしては,(1)適当な1辺の長さ,(2)三角点のうちの1点(測地原点)の経度と緯度,(3)測地原点から特定の三角点方向の方位角(真北から東まわりに測った角)の3種である。(1)は形だけしかわかっていない三角網にスケールを与えるものであり,これにより三角網の大きさが決定される。この辺は基線と呼ばれ,基線測量により求められる。(2)と(3)は,天文測量により与えられる。このうち(2)は,三角網が地球上のどの位置にあるかを指定する。この段階では三角網のうち測地原点のみが地表に固定されていて網自体の方向はわからない。いいかえれば,三角網は測地原点のまわりに回転することができる。この回転を止めるために(3)の方位角(原方位角)を指定するのである。
以上の手続きにより三角網は地球上に固定されたわけであるから,三角網に含まれるすべての三角点の経度,緯度を計算することができる。例えば,原方位角の目標となった測地原点の隣の点については,測地原点からの距離と方向がわかっているので,簡単に経度,緯度を求めることができる。さらにこの2点に隣接する点も同様にして位置を決定することができる。このようにして,測地原点から三角網の外縁に向かって次々と三角点の経度,緯度が求められてゆくのであるが,測地原点から遠く離れた三角点では,途中の水平角観測値の誤差が積み重なって,計算された経度,緯度は誤差の大きいものになる。このため,大きな三角網では,基線は1ヵ所だけではなく数ヵ所設置される。また方位角も測地原点以外でも観測されることもある。日本のように外国と海で隔てられているような地域に,新しく三角網を設置して三角測量で三角点の位置を求める場合は,以上の方法を採用するのが普通であるが,測量地域内に既に経緯度の決められた三角点(既知点)がある場合は,三角測量で水平角観測を行うだけで三角点の位置を決めることができる。例えば,既知点が2点あれば,(1)(2)(3)で与えられるべき情報のすべてが得られるのである。すでに三角測量の終わった地域の隣で新しく三角測量を行う場合や,目のあらい三角網の中にさらに密度高く三角点を設置して,その経度,緯度を求める場合にはこの方法が採用される。
日本における代表的な三角測量は,明治から大正にかけて行われた一等三角測量であろう。この測量は国土の地理的様相を把握し,日本全体の精密な地形図を作成するための基準を決定するために行われた。一国全体にわたるような大きな地域の三角測量を行う場合は,能率的に高精度を確保するために最初は目のあらい三角網について三角測量を行って三角点の経度,緯度を求めておき,この値に基づいて逐次目の細かい網を測量してゆく方式が採用される。日本の三角点には網の細かさに応じて,一等から四等までの三角点がある。一等三角測量は一等三角本点によって構成される最も目のあらい一等三角網の測量である。一等三角測量では三角網に含まれるすべての夾角が経緯儀によって測定された。測地原点は東京(東京都港区麻布台,旧東京天文台構内にある子午環の中心点),原方位は測地原点から千葉県内の一等三角点鹿野山に向かう方向で,方位角(真北から時計回りに測った角度)は156°25′28″.442と定められている。基線は全国14ヵ所に設置された。一等三角補点,二等,三等,四等の各三角点は,一等三角本点の値をもとにして三角測量が行われ,その経度,緯度が決められている。
執筆者:吉村 好光
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「三角測量」の意味・わかりやすい解説
三角測量
さんかくそくりょう
triangulation
地上の互いに見通せる3点を選んで三角形をつくり、その1辺の長さおよび2夾角(きょうかく)を測定して、三角法により他の2辺の長さや頂点の位置を求める古典的な測量法。三角形を多数接続させて広い範囲の測量を能率よく、かつ精度よく行える。このような三角形の集合を三角網というが、鎖状につないだ場合は三角鎖(さ)といい、広大な地域の骨組みとしての三角測量の場合に使われる。
三角網あるいは三角鎖の測量では少なくとも1辺の長さを実測しておかねばならない。これを基線といい、この長さの測定には25メートルのインバール(温度によって伸び縮みしにくい合金)製の尺が用いられたが、1970年代には精密な電磁波測距儀により三角形の辺長が直接測定できるようになった。また少なくとも1点の地球上の位置と1方向の方位とは与えておかなければならず、これは天文測量により決定される。
精密な三角測量では3内角を観測してその和を求め、観測誤差の点検調整を行うが、1辺が数十キロメートルに及ぶ地球上の三角形は球面三角となり、3内角の和は180度よりは多少大きくなる。これを球過量あるいは球面過剰といい、三角形の面積が100平方キロメートル(1辺の長さ約14キロメートル)の場合の球過量は約0.5秒、1辺の長さ約40キロメートルでは約8秒となる。
三角網には一等、二等、三等、四等などの等級があり、しだいに細かい網をつくって上級の網のすきまを埋めていく。これらの網の調整計算には膨大な計算量が必要なので、適当な大きさの三角網群にくぎってそれぞれ別個に計算を行っていたが、1970年代にはコンピュータの利用により、日本全国をいちどきに調整計算することができるようになり、再計算もされた。また三角網が大きくなると、観測誤差が累積して網にねじれが生じるので、所々の三角点で天文測量を実施して、このねじれを規制する。この点をラプラス点という。1970年代以降、精密な電磁波測距と電子計算機による全国の厳密調整計算による再測も行われたが、1990年代以降はGPS衛星を用いた測量により三角網の再測が行われている。
[尾崎幸男・辻 宏道 2016年11月18日]
百科事典マイペディア 「三角測量」の意味・わかりやすい解説
三角測量【さんかくそくりょう】
→関連項目三角関数|三角形|視差|測地衛星|測地原点|測距儀|地図|トラバース測量
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「三角測量」の意味・わかりやすい解説
三角測量
さんかくそくりょう
triangulation; triangulation survey
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
最新 地学事典 「三角測量」の解説
さんかくそくりょう
三角測量
triangulation
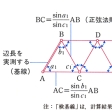
水平位置を求めるため最もふつうに行われる測地測量。地上に設置された三角点は三角形をつくり,一連の三角形は三角網を構成する。この三角網のなかの少なくとも一辺は実測されなくてはならない。三角形の内角を経緯儀で測定すれば,この三角網の形と大きさが決まる。三角網内の一点Bの経度・緯度がわかっており,また基線ABの方位角がわかっていれば,三角網の地球上の位置が決まる。そして三角網の計算を行い,点Cの位置が決まる。加えてACの長さや方位角も決まる。以上は未知の点Cの位置を求めるために最小限必要な手続きであるが,実際には,例えばCDという基線を設けたり,独立に天文測量によってCAの方位角を測定したりして,既知量から計算で求められたCDの長さやCAの方位角と比較することにより,三角測量の精度を点検する。そして,最終的には最小2乗法で最も誤差の少ない各点の位置を決定する。三角測量は,その目的によって,通常一等三角測量から四等まで区分される。日本の場合,三角形の一辺の大きさは,一等三角測量で45km,二等で8km,三等で4km,四等で2km程度。以上は測地網をつくるための三角測量であるが,三角測量を繰り返して実施すれば地殻の水平変動を調べうるので,三角測量はこの目的のためにも実施される。参考文献:斎藤暢夫(1951) 三角測量,オーム社
執筆者:藤井 陽一郎
出典 平凡社「最新 地学事典」最新 地学事典について 情報
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...