放物運動（読み）ホウブツウンドウ（英語表記）projectile motion

デジタル大辞泉

ほうぶつ‐うんどう〔ハウブツ‐〕【放物運動／^×抛物運動】

空中に斜めに投げ上げた物体が、空気の抵抗がないものとすれば、重力の作用で放物線を描く運動。

出典　小学館

精選版 日本国語大辞典

ほうぶつ‐うんどうハウブツ‥【放物運動・抛物運動】

1. 〘 名詞 〙 地球上で投げられた物体の運動。空気の抵抗を無視すれば、物体に働く力は重力だけとなり、その軌道は放物線となる。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

放物運動
ほうぶつうんどう
projectile motion

一様な重力のある空間に投げ出された物体の行う運動で、空気による抵抗を無視した場合その軌跡は放物線を描く。

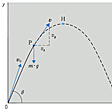
　質量mの物体（厳密には質点）が、水平とθの角をつくる方向に速さv₀で投げられた場合の運動を考察する（図）。軌道上の任意の点でのニュートンの運動方程式は、重力（＝m・gここでgは重力加速度）がつねに垂直方向にのみ作用していることから、水平（x軸）と垂直（y軸）の方向に分けられ、
　　m・dv_x/dt＝0,
　　m・dv_y/dt＝－m・g
である。ここで添字xおよびyは、速度ベクトルvの各成分を指定し、tは時間変数である。これらは簡単に積分できて
　　v_x＝c₁,
　　v_y＝－g・t＋c₂
で与えられる。定数c₁およびc₂は、時刻ゼロでの速度ベクトルv₀＝(v₀cosθ,v₀sinθ)を与えることによって決められ、
　　v_x＝v₀cosθ,
　　v_y＝－g・t＋v₀sinθ
となる。これらは、任意の時刻tにおける質点の速度を与える。そのときの質点の位置はさらに微分方程式
　　dx/dt＝v_x＝v₀cosθ,
　　dy/dt＝v_y＝－g・t＋v₀sinθ
を積分して、
　　x＝v₀cosθ・t＋d₁,
　　y＝－g・t²/2＋v₀sinθ・t＋d₂
で与えられる。ここで時刻ゼロで質点が原点、すなわちx＝y＝0であることを考慮すると、積分定数はd₁＝d₂＝0となる。以上のことから、空間に投げられた質点の任意の時刻における力学的運動状態、すなわち位置と速度がtの関数として一義的に決められることがわかる。このことは古典力学で一般的に成り立つことである。質点に働く力が与えられているならば、その質点の将来の力学的状態（位置と速度）は、ある時刻（たとえばt＝0）での値によって一義的に決まる。これを古典力学の因果律という。

　質点が描く軌道は、xとyの式からtを消去して、xとyの関係を求め
　　y＝x・tanθ－g・x²/2v₀²cos²θ
となり、いわゆる放物曲線となる。最大到達点Dまでの距離は、ふたたびy＝0となるxの値であるから、x＝v₀²sin2θ/gで与えられ、最高到達点Hの高さは、dy/dx＝0となる点のyの値であるから、y＝v₀²sin²θ/2gで与えられる。

［阿部恭久］

『飯島徹穂・佐々木隆幸・青山隆司著『アビリティ物理　物体の運動』（1999・共立出版）』

[参照項目] | 放物線

放物運動（最高到達点と最大到達点）〔図…

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

放物運動 (ほうぶつうんどう)
projectile motion

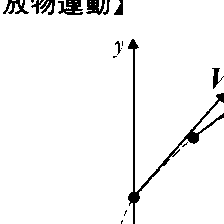
地上から空中に投げられた物体の運動。あまり広くない範囲を運動する場合には，物体が受ける重力は一定で，大きさは質量に比例し，鉛直下向きであるから，空気の抵抗など重力以外の力を無視してよければ，物体（の重心）は鉛直下向きに一定の加速度（重力加速度）をもった運動を行う。その速度の時間変化は図のようになり，毎秒g＝9.8m・s⁻¹の割合で下向きに変化する。初速度を含む鉛直面内で水平にx軸，鉛直上向きにy軸をとれば，速度の時間変化は，初速度のx方向およびy方向の成分をそれぞれV_0x，V_0yとして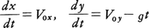，で与えられ，x方向は等速運動x＝V_0xtであることがわかるが，y方向は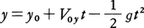，であるから（y₀はt＝0の高さ），t＝x/V_0xを代入すると，yとxの関係式として放物線を表す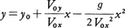，が得られる。これは物体の運動する軌道を表す。速度に依存する抵抗があると，速度の水平成分はしだいに0に，鉛直成分は下向きの一定値（重力と抵抗がつり合うような速さで終端速度という）に近づく。ボールや弾丸が回転していれば，速度に垂直な方向の力も作用し，運動はさらに複雑になる。放物運動は，弾道学として昔から詳しく研究されてきているが，人工衛星やミサイルの発達に伴って，地球の丸さを考えに入れるような大きなスケールで調べられるようになってきている。
執筆者：小出 昭一郎

図－放物運動

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の放物運動の言及

【運動】より

…質量
【重力場での運動】
　例えば(3)式から，質量mの物体に働く重力の大きさは，物体によらず一定である落下の加速度g(＝9.8m/s²)を用いてmgと表せる。逆に重力の作用の下での物体の運動は，自由落下，放物運動のどちらについても(3)式の右辺のFを鉛直下向きに向いた大きさmgのベクトルとしてこの運動方程式(位置座標に関して2階の常微分方程式)を解き，物体の位置r(t)を時間tの関数として求めることによって理解することができる。落下運動の場合にはその鉛直方向の位置座標z(t)は，t＝0における位置座標および鉛直方向の速度をそれぞれz₀,w₀として，z(t)＝z₀＋w₀t－1/2gt²で，また放物運動はこれと水平方向の運動x(t)＝u₀tの組合せとなる(u₀はt＝0における水平方向の速度)。…

※「放物運動」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」