標本分布（読み）ひょうほんぶんぷ（その他表記）sampling distribution

改訂新版　世界大百科事典

標本分布 (ひょうほんぶんぷ)
sampling distribution

数理統計学において，統計量の分布をいう。有限個の要素を含むある集合が与えられたとき，この集合から1個の要素を無作為に選び出し，その要素のある特性量ξの値を観測しそれを再びもとの集合にもどす。この実験では，どの要素が選ばれる可能性もすべて等しくなる（これを無作為という）ようにくふうされているものとする。与えられた集合のことを母集団といい，その要素のことを個体という。上の実験をn回繰り返すとき観測される1組の個体を母集団からの無作為標本という。

　個体そのものについては関心がなく，特性量ξのとるいろいろな値と，これらの値の分布だけに注目することが多い。このような場合には，個体そのものでなく，それに対応するξの値が母集団を構成していると考えると便利である。母集団の各個体にそのξの値を記入したカードを対応させると，母集団はそれらのカードの入った壺であるということができる。n個の観測値の列x₁，x₂，……，x_nはこのξ-値が記入されたカードの母集団からの無作為標本とみなせる。特性量ξは，ランダムに変化する量であり，確率変数である。カードは有限個であるから，確率変数ξは有限個の値しかとれない。ξが特定の値に等しい確率は，上に述べた実験方法の下では自然に定まっている。すなわち，確率変数ξの分布は，ある離散分布である。観測値の列x₁，x₂，……，x_nは，ξと同じ分布をもつ独立確率変数列の実現値であることが実験の条件から導びかれる。

　上に述べたように，ξの分布は現実には離散分布であるが，カードの数Nが非常に大きいときは，連続分布に近くなることが多い。カードを適当に入れかえるとかってな連続分布に近づけることができる。離散分布より連続分布のほうが理論的解析を展開しやすい場合が多いので次のような仮想的状況（モデル）を設定する。母集団がカードの集合であることは忘れよう。母集団は無限集合（無限母集団）であり“無作為”に選び出したξの値の分布は，連続分布または離散分布であるとしよう。n個の観測値の列x₁，x₂，……，x_nは，ξと同じ分布をもつ独立確率変数列の実現値であるとする。上に述べたことは，直ちにk次元確率変数（kは任意）の場合に拡張できる。この仮想的母集団におけるすべての個体は，k個の数値の組によって特徴づけられ，k次元確率変数の実現値（観測値）の列は，このような無限母集団からの無作為標本とみなされる。

　特性量ξが何らかの分布関数F（x）をもつと考えてよいことは，これまでの議論によって承認されよう。ところでξの分布は一般には未知であるが，これをいかにして求めたらよいだろうか。確率変数ξのn個の観測値x₁，x₂，……，x_nを考えよう。ここで，標本の分布関数F^＊（x），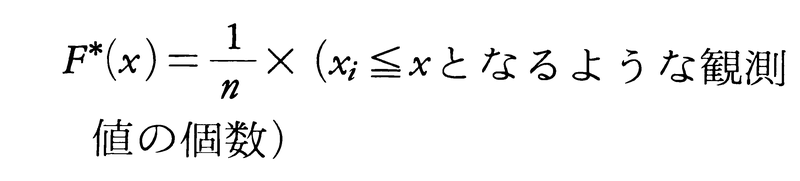

を考える。すなわち，F^＊（x）はn個の観測の列において，ξ≦xとなる事象の起こる相対度数をあらわしている。x₁，x₂，……，x_nをξと同じ分布をもつ独立確率変数列ξ₁，ξ₂，……，ξ_nの実現値とみなすと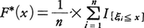，と書ける。ここで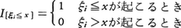，である。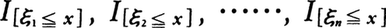は独立確率変数列で，その期待値はつねにF（x）であるから，大数の法則によってn→＋∞のとき確率1で，

　F^＊（x）→F（x）

となる。母集団の分布を，この事実に基づいて，経験的に推測することは可能である。一方で，母集団の分布が（仮説の指定する）特定の分布であるかどうか仮説検定をすることができる。これを適合度検定という。

　特性量ξの性格から，ξの分布は，正規分布，一様分布，指数分布，ポアソン分布などと自然に定まる場合もある。

　以上のようにして，特性量ξの分布がわかったとしよう。ξ₁，ξ₂，……，ξ_nをξと同じ分布に従う独立確率変数列とする。数理統計学では，一般に確率変数g（ξ₁，ξ₂，……，ξ_n）が議論の対象となる。この確率変数g（ξ₁，ξ₂，……，ξ_n）を統計量という。統計量の分布は，ξの分布関数F（x）から一意的に定まることは明らかである。このg（ξ₁，ξ₂，……，ξ_n）の分布を標本分布という。ところが，g（ξ₁，ξ₂，……，ξ_n）の分布が一般的に明らかになるのは，gがξ₁，ξ₂，……，ξ_nの一次式で書きあらわされている場合くらいである。gが一次式のときは，独立確率変数の和の分布を求めることになる。標本分布の精密な形について，一般的性格をもった結果はほとんど知られていない。例外的に，母集団の分布が（任意次元の）正規分布である場合，系統的な結果が得られている。χ²-分布，スチューデント分布，フィッシャーのz-分布などの研究は，この流れの中に位置づけられる。母集団の分布が一般の場合，特殊なgに対して，nが非常に大きければ，g（ξ₁，ξ₂，……，ξ_n）の分布が漸近的に正規分布となることが，中心極限定理により知られている。
執筆者：清水 昭信

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

標本分布
ひょうほんぶんぷ

統計的推測を行う場合、母集団から大きさnの任意標本をとり、たとえばその標本の相加平均など、標本のある関数を考え、これがどのような確率分布をもつかが問題となることが多い。すなわち、n個の確率変数X₁、X₂、……、X_nが独立で、各X_iは同一の確率分布をもつとし、F(x₁,……,x_n)を与えられたn変数の関数として、確率変数Y=F(X₁,……,X_n)の確率分布を決定することが問題となる。Yの分布のことを標本分布という。

　以下では、X₁、……、X_nは独立で、各X_iの分布は正規分布であると仮定する。

（1）X_iがすべて同一の正規分布N(m,σ²)をもてば

の分布は正規分布N(m,σ²/n)である。

（2）X_iがすべて同一の正規分布N(0,1)をもてば
　　Y=X₁²+X₂²+……+X_n²
の確率密度をk_n(x)とすると

である。ただしΓ(x)はガンマ関数を表す。このk_n(x)を確率密度とする確率分布を自由度nのχ²（カイ二乗）分布という。

（3）X_iがすべて同一の正規分布N(m,σ²)をもてば

の両者は独立で、(n/σ²)S²の分布は自由度(n-1)のχ²分布である。

（4）X、Y_nが独立で、Xが正規分布N(0,1)、Yが自由度nのχ²分布をもつならば

の確率密度は

である。このZ_nの分布を自由度nのt分布という。

（5）X_m、Y_nが独立で、それぞれ自由度m、nのχ²分布をもつならば

の確率密度f_mn(x)は

である。このZの確率分布を自由度m、nのF分布という。

［古屋　茂］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

標本分布
ひょうほんぶんぷ
sampling distribution

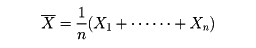
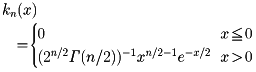
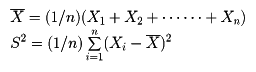
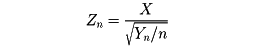
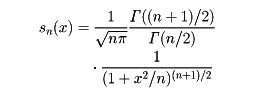
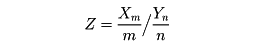
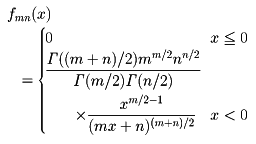
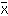無作為抽出を無限回にわたって繰返したときに，標本平均のような統計量が示す度数分布を，その統計量の標本分布という。社会調査に応用される標本調査法にとっては，特に次の2つの定理が重要である。(1) 平均の標本分布　母平均が m，母標準偏差が σ，大きさが M の有限正規母集団から，大きさ N の無作為標本を抽出するとすれば，標本平均 の標本分布は平均が m，標準偏差が 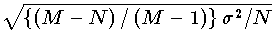の正規分布を示す。(2) 比率の標本分布　大きさ M の有限母集団において，ある標識をもっている比率が P のとき，この母集団から大きさ N の無作為標本を抽出するとすれば，標本比率 p の標本分布は平均 P，標準偏差 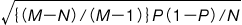の正規分布を示す。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の標本分布の言及

【フィッシャー】より

…第1は統計的推測とくに推定(統計的推定)の基礎理論の建設で，最尤（さいゆう）推定法の導入とその大標本のもとでの有効性の証明，推定量の効率の尺度としての情報量の定義，推測確率の概念の導入などがある。第2は統計量の標本分布に関連し，処女論文における相関係数の精密標本分布の導出をはじめ，偏相関係数，Z分布，分散共分散行列の固有根の分布などを求めた。第3は統計的実験計画法の創出で，ロザムステッドにおける経験にもとづき，実験誤差を含む条件のもとでの実験の計画およびデータの解析法を確立した。…

※「標本分布」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」