固有振動（読み）コユウシンドウ（その他表記）proper vibration

デジタル大辞泉

こゆう‐しんどう〔コイウ‐〕【固有振動】

振動体を自由に振動させたときの、その振動体が固有に示す一定数の振動。

出典　小学館

精選版 日本国語大辞典

こゆう‐しんどうコイウ‥【固有振動】

1. 〘 名詞 〙 振動体が自由に振動するときの長さ、質量、弾性などの物理的性質で定まる一定の振動数をもつ振動。弦楽器では、弦の太さや張力を変えて弦の固有振動数を調整する。
   1. [初出の実例]「鉄針と竹針とによる音色の相違は恐らく針自身の固有振動にも関係するだらうし」(出典：蓄音機（1922）〈寺田寅彦〉)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

固有振動 (こゆうしんどう)
proper vibration

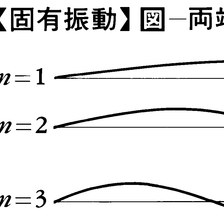
両端を固定した弦，管の中の空気，つなぎ合わせた振子など，物体またはその集りを振動させるときには，いくつかの特定の振動数の振動のみが発生する。これらを固有振動といい，その振動数を固有振動数という。固有振動は，振動する物体の形・構造，それを形づくっている物質の密度・弾性係数，物体の支えかたなどによって定まる。例えば長さl，単位長さ当りの質量ρの弦に張力Tを加え，両端を固定して振動させるときの固有振動数ν_nは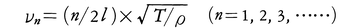，となる。これらの振動のようすを図に示す。図からわかるように弦の固有振動は，弦の上に生ずる定常波で両端が節になっているものにほかならない。またこのようにいくとおりもの固有振動がある場合には，その中で振動数がもっとも低いものを基本振動fundamental vibration，その他を倍振動という。実際に物体が振動する際には，一般に基本振動といくつかの倍振動が重なり合った振動が起こる。なお，物体に外から周期的な力が加わる場合，その振動数が物体の固有振動数に近いほど，物体の振動は激しくなる。この現象を共振という。
→振動
執筆者：有山 正孝

図－両端を固定した弦の固有振動

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

固有振動
こゆうしんどう
natural vibration

系が自由な状態で振動するときに現れる固有の振動形式。系は構造や内部条件で決るいくつかの固有振動数をもつ。弦や気柱の振動などのように固有振動数が倍数関係にある場合には，固有振動の組のなかで最小振動数のものを基本振動，それの整数倍の振動数のものを倍振動という (→基本振動 ) 。板の固有振動の様子を示すものにクラドニ図形がある。時計は振り子，ひげぜんまい，水晶棒または水晶板などの固有振動によって時を刻む。原子時計は原子または分子の特定のエネルギー準位間の遷移の固有振動を利用した非常に高精度な時計であって，セシウム原子時計は時間の単位である秒を定義するのに用いられる。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

固有振動【こゆうしんどう】

→振動

出典　株式会社平凡社

世界大百科事典（旧版）内の固有振動の言及

【音】より

…外から振動的な力が加えられているときの振動を強制振動といい，これに対して，外力をとり除いたあとでの振動が自由振動である。自由振動の状態は，物体の形状寸法と弾性的な性質によって決まる特定の振動数と振動の状態をもった固有振動によって規定される。固有振動の数は無限に多く，その組合せによって自由振動の状態が決まる。…

【振動】より

…弦の単位長さあたりの質量をσとすると，弦を伝わる波の速さvは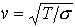で与えられることがわかっており，これと定常波の波長λ_n，振動数ν_nとの関係ν_n＝v/λ_nを用いると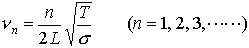，である。これらをこの弦の固有振動といい，とくにν₁を基本振動，ν₂以上を倍振動という。これらは先に述べた基準振動に対応するものである。…

【量子力学】より

…
［定常状態］
　シュレーディンガー方程式の解のなかには，波動が空間のあらゆる点でいっせいに足並みそろえて振動するようなものがある。これは，2点の間にピーンと張った弦の振動の場合なら固有振動に相当するもので，量子力学の波動の場合にもその振動数は特定の一連の値(固有振動数)ν₀，ν₁，……に限られる。こうしたψの固有振動は，それぞれ量子力学的粒子のエネルギー確定の運動を表し，それをしている粒子は定常状態にあるといわれる。…

※「固有振動」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」