精選版 日本国語大辞典 「大数の法則」の意味・読み・例文・類語
たいすう【大数】 の 法則(ほうそく)
日本大百科全書(ニッポニカ) 「大数の法則」の意味・わかりやすい解説
大数の法則
たいすうのほうそく
確率に関する法則。ベルヌーイの大数の法則と、大数の強法則とがある。さいころを多数回投げると、6の目が出るのは全体の回数のほぼ1/6であることが期待される。この事実を一般化して考える。ある試行において事象Eのおこる確率をpとし、この試行を独立にn回繰り返すとき事象Eのおこる回数をXnで表すと、nを十分大きくとれば、相対度数Xn/nは、例外的な場合を除けばほぼpに近い。これをベルヌーイの大数の法則という。この内容をさらに詳しくいうと次のようになる。上記のXnは確率変数で、その確率分布は二項分布B(n,p)であって、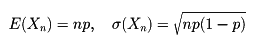
となる。確率変数Yn=Xn/nに対して、チェビシェフの定理を適用すると、σn=σ(Xn)として
P(|Yn-p|≧(cσn)/n)
≦1/c2
となる。ただしcは1より大きい任意の数である。ここでε=cσn/nと置けば
P(|Yn-p|≧ε)
≦p(1-p)/nε2
したがって任意に与えられた二つの正数ε、ηに対してnを十分大きくとれば(p(1-p)/ηε2<nのように)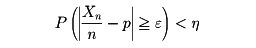
が成り立つ。これがベルヌーイの大数の法則である。
ベルヌーイの大数の法則について見方を逆にすると、多数回の実験による相対度数Xn/nによってp(その値が未知であるときにも)の値が推定されるという考えに導かれる。ド・モアブルもこの考えに到達していた。ベルヌーイの大数の法則は実質上は有限の場合の話である。nが無限に大きい場合はどうなるか。初めのさいころの例についていえば、n回のうちに6の目が出る回数をXnとすると、次の関係が成り立つ。
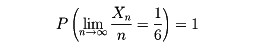
これはボレルが初めて証明した定理で、ベルヌーイの大数の法則より深い内容をもち、大数の強法則とよばれている。一般の形でいえば次のようになる。X1、X2、……、Xn、……は確率変数で、各Xiの分散は一定値以下であるとする。σ2(Xi)≦σ2<∞、またX1、X2、……、Xn、……は独立とする。このとき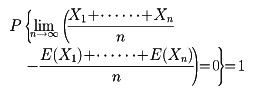
が成り立つ。
[古屋 茂]
改訂新版 世界大百科事典 「大数の法則」の意味・わかりやすい解説
大数の法則 (たいすうのほうそく)
law of large numbers
ベルヌーイ型の大数の弱法則とコルモゴロフの大数の強法則とがある。
X1,X2,……,Xnを独立で,平均値がmで標準偏差がσである同じ分布に従う確率変数とする。それらの相加平均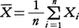 は,平均値はやはりmであるが,標準偏差はσ/\(\sqrt{n}\)の確率変数である。これにチェビシェフの不等式をあてはめると,かってな正数εに対して,
は,平均値はやはりmであるが,標準偏差はσ/\(\sqrt{n}\)の確率変数である。これにチェビシェフの不等式をあてはめると,かってな正数εに対して,
P(|-m|>ε)≦σ2/(nε2)
である。nを大きくすれば右辺は0に近づく。よってがmとε以上違う確率はnが大きければ十分小さい。これがベルヌーイによる大数の弱法則である。
例えば,毎回成功する確率がp,失敗する確率がqである試行を独立にn回繰り返した場合を考えよう。各Xiがi回目の試行に対応するとし,成功には1を,失敗には0をあてはめると,P(Xi=1)=p,P(Xi=0)=qである。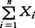 は,平均値がnp,標準偏差が
は,平均値がnp,標準偏差が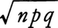 の二項分布に従う。このとき大数の弱法則は,がその平均値pとε以上違う確率はnが大きければ非常に小さいことを示す。なお,この法則は
の二項分布に従う。このとき大数の弱法則は,がその平均値pとε以上違う確率はnが大きければ非常に小さいことを示す。なお,この法則は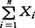 がnpに近いことを示すものではない。また,>pであるからといって,以後の試行でこれを補正しようとして成功する場合の回数が減少することを保証するものでもない。
がnpに近いことを示すものではない。また,>pであるからといって,以後の試行でこれを補正しようとして成功する場合の回数が減少することを保証するものでもない。
大数の強法則は,A.N.コルモゴロフによって示されたものであるが,上記の弱法則よりも強い主張として次の結果がある。Xiは最初のように一般的な確率変数として,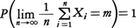 大数の法則を統計的観察に適用すれば,大量を観測するほど,その相加平均が真の値に近づくことを意味する。
大数の法則を統計的観察に適用すれば,大量を観測するほど,その相加平均が真の値に近づくことを意味する。
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「大数の法則」の意味・わかりやすい解説
大数の法則
だいすうのほうそく
law of large numbers
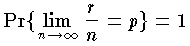 という強法則もある。
という強法則もある。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「大数の法則」の意味・わかりやすい解説
大数の法則【たいすうのほうそく】
→関連項目保険
出典 株式会社平凡社百科事典マイペディアについて 情報
損害保険用語集 「大数の法則」の解説
大数の法則
出典 自動車保険・医療保険のソニー損保損害保険用語集について 情報
法則の辞典 「大数の法則」の解説
大数の法則【law of great numbers】
保険基礎用語集 「大数の法則」の解説
大数の法則
出典 みんなの生命保険アドバイザー保険基礎用語集について 情報
ブランド用語集 「大数の法則」の解説
大数の法則
出典 (株)トライベック・ブランド戦略研究所ブランド用語集について 情報
世界大百科事典(旧版)内の大数の法則の言及
【生命保険】より
… 保険契約者から徴収される保険料は,保険者(保険会社の場合が多い)が算定し,集め,管理する。ところで,この保険料は,大数の法則による年齢ごとの死亡確率をはじめ,次のような原理にもとづいて計算される。 (1)大数の法則 独立な試行を多数回反復した場合に得られる標本平均は母集団平均に近い値をとるという法則である。…
【保険】より
…リスクにさらされた人が,保険団体を形成して,自己の所定のリスクを,大数の法則を応用して計算された保険料の形に変え,これに移転しプールすることによって,偶然な事故発生の場合に損害・損失が保険団体から補償される経済制度である。リスクとは事故により損害・損失を受ける可能性(あるいは不確実性)がある状態をいう。…
※「大数の法則」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

