ウィーンの変位則（読み）ウィーンノヘンイソク（その他表記）Wien's displacement law

デジタル大辞泉

ウィーン‐の‐へんいそく〔‐ヘンヰソク〕【ウィーンの変位則】

1893年にドイツの物理学者ウィーンが発見した、黒体からの熱放射（黒体放射）に関する法則。黒体の絶対温度をTケルビン、放射のエネルギー密度が最大になる波長をλラムダメートルとすると、λT＝0.002898という関係式で表され、λはTに反比例することを示した。ウィーンの公式。

出典　小学館

改訂新版　世界大百科事典

ウィーンの変位則 (ウィーンのへんいそく)
Wien's displacement law

物体の温度をあげていくと（暗いところで見れば600℃くらいから）鈍い赤色に光り始め，やがて青白色を呈し，ついには白熱化する。これは，物体の放射する光の波長が温度の上昇につれて短いほうに変位していくためである。とくに黒体からの放射ないしは空洞放射では簡明な法則性があり，絶対温度Tの熱平衡状態では，（放射の単位体積につき）各波長λに対して単位波長幅当りの放射エネルギー（スペクトル密度）u_t（λ）が最大となる波長λ_mはTに反比例し，λ_mT＝一定となる。これがウィーンの変位則である。右辺の定数は，光速c，プランク定数h，ボルツマン定数kという三つの基本定数で表され，（ch/k）/4.9651＝2.8978×10⁻³m・Kである。この法則はS.P.ラングリーやH.F.ウェーバーらにより1880年代の半ばから実験的に推測されていたが，93年にW.ウィーンが理論的に証明した。彼は，空洞放射の満ちた筒にピストンを押し込む思考実験を考えて，動くピストン面で放射が反射されるときのドップラー効果による波長変化λ→λ′を求め，他方で放射圧に抗してピストンを押し込むときする仕事とシュテファン=ボルツマンの法則とから温度変化T→T′を求めて，一般的にλ′T′＝λTが成り立つことを示したのである。これは2変数の関数u_t（λ）を（規格化因子N_tは別として）1変数λTの関数fできまる形u_t（λ）＝N_tf（λT）にまで追いつめたことである。N_tはシュテファン=ボルツマンの法則

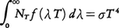からN_t＝σT⁵

と定まる（σはシュテファン=ボルツマンの定数）。したがって，定数σをfに含めればu_t（λ）＝T⁵f（λT）と表せる。これはスケーリング則の一つであり，これをウィーンの変位則と呼ぶこともある。この結果は20世紀初頭の作用量子発見に導いた空洞放射の研究過程で大きな力になった。空洞放射のスペクトル密度u_t（λ）は空洞の形にも壁の材料にもよらないから，関数fは普遍的なもので基本的重要性をもつとみなされたのである。
執筆者：江沢 洋

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ウィーンの変位則
うぃーんのへんいそく
Wien's displacement law

絶対温度Tの黒体から放射される、エネルギー密度が最大になる波長（λ_max）が、Tに反比例するという法則。1893年にウィーンが熱力学をもとに導いた。絶対温度をT（K）、放射エネルギー密度が最大になる波長をλ_max（センチメートル）とすると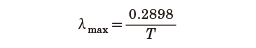

と表される。0.2898は比例定数である。

　このことから、放射されるエネルギー密度が最大になる波長を測定することにより、その物体の温度が判明する。直接に温度を測定することができない場合、たとえば、溶鉱炉などの高温の物体の温度を正確に測定する際に重要な方法である。温度が高くなるほど放射される波長は短くなり、太陽表面温度（約5780K）では500ナノメートルになる。

［山本将史　2021年7月16日］

[参照項目] | ウィーン | 黒体 | 絶対温度 | 熱力学

出典　小学館　日本大百科全書(ニッポニカ)

最新 地学事典

ウィーンのへんいそく
ウィーンの変位則

Wien’s law of radiation

黒体放射エネルギースペクトルのピーク波長と温度の関係式。1896年にヴィルヘルム・ウィーン（Wilhelm Wien）によって提唱された。ピーク波長は黒体表面の絶対温度に反比例する。太陽の表面温度5,780Kの場合のピーク波長は約500nm（可視光域），地球の表面温度300Kの場合のピーク波長は約10µm（赤外域）となる。前者を短波放射あるいは日射，後者を長波放射あるいは地球放射という。プランクの法則を波長で微分することで導出できる。参考文献：田中博（2017） 地球大気の科学，共立出版

執筆者：梶野 瑞王

参照項目：黒体放射
参照項目：地球放射
参照項目：プランクの法則

出典　平凡社「最新 地学事典」

百科事典マイペディア

ウィーンの変位則【ウィーンのへんいそく】

いろいろな温度の黒体が放出する放射エネルギーのスペクトル分布をとってみると，その極大値に相当する波長λ(/m)は黒体の絶対温度Tに反比例し，λ(/m)T＝一定（0.287cm・K）になるという法則。W.ウィーンの発見。高温測定に利用。長波長側では成り立たなかったが，のちにM.プランクが改良する。
→関連項目空洞放射｜黒体放射｜シュテファン=ボルツマンの法則

出典　株式会社平凡社