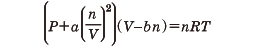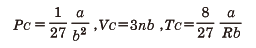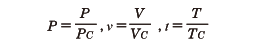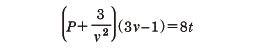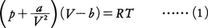ファン・デル・ワールスの状態方程式
ふぁんでるわーるすのじょうたいほうていしき
van der Waals' equation of state
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
ファン・デル・ワールスの状態方程式 (ファンデルワールスのじょうたいほうていしき)
van der Waals' equation of state
オランダの物理学者ファン・デル・ワールスが1873年に提唱した状態方程式で,1molの物質に対して,
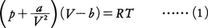
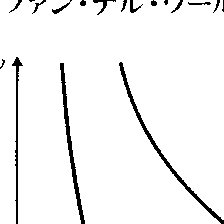
と表される(pは圧力,Vは体積,Rは気体定数,Tは絶対温度)。この方程式は,理想気体からのずれを,(1)定数bで気体分子の大きさの影響を表し,(2)定数aで分子間引力の効果を取り入れるという考え方に立脚して導かれた。この状態方程式の特徴は,Tc=8a/27bRで与えられる臨界温度Tcの存在である(臨界点では(1)式のほか,(∂p/∂V)t=0,(∂2p/∂V2)t=0が成立することから求められる)。T>Tcでは図のように等温線はVの単調減少な関数を表し,理想気体と似たふるまいを示す。これに反して,T<Tcだと等温線に極小点A,極大点Bが出現する。図のように,斜線部の面積が等しくなるように水平線CDをひき(マクスウェルの規則),点Dより右側の等温線は気体,点Cより左側の等温線は液体の状態を表すと解釈されている。また,点Cと点Dとの間は気体と液体とが共存する状態を示す。このように,ファン・デル・ワールスの状態方程式を用いると,臨界温度の存在,気体から液体への凝縮現象など,現実の物質で観測される事実が理解できる。
執筆者:阿部 龍蔵
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
ファン・デル・ワールスの状態方程式
ファン・デル・ワールスのじょうたいほうていしき
van der Waals' equation of state
1873年 J.ファン・デル・ワールスによって示された実在気体に関する状態方程式。気体の圧力を p ,1mol の体積を V ,絶対温度を T とすると,次のように表わされる半実験式である。
(p+a/V2)(V-b)=RT
a ,b は気体の分子間力によって決る定数,R は気体定数である。この状態方程式は実在気体の理想気体からの偏差をある程度まで説明でき,気相 - 液相間の転移や臨界状態の研究に用いられた。図は種々の温度に対する等温曲線で,点線の内側は気体と液体が共存する領域である。曲線tについてみると,まず気体領域で体積を減じると圧力が徐々に増し,A 点に達する。実際の変化は直線 ABC の方向に進み,この間は気体の液化が進んで気体と液体とが共存している。全部が液化してしまう点が C である。液体は体積を少し縮小するのにも大きな力が必要であるから,圧力が急激に増大する。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
ファン・デル・ワールスの状態方程式【ファンデルワールスのじょうたいほうていしき】
ファン・デル・ワールスが1873年に提唱した気体の状態方程式の一つ。気体分子間の引力,気体分子自身の大きさを考慮に入れたもので,気体の圧力をp,その1モルの体積をv,絶対温度をTとすると (p+a/v2)(v−b)=RTで表される(Rは気体定数,aおよびbは気体の種類によって決まる定数)。
→関連項目気体|ファン・デル・ワールス力
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
世界大百科事典(旧版)内のファン・デル・ワールスの状態方程式の言及
【状態方程式】より
…ただし,a,bは気体の種類によって決まる定数で,とくにa=b=0とおけば(2)は(1)に帰着する。(2)を[ファン・デル・ワールスの状態方程式]という。この方程式は,(1)と異なり,臨界点の存在とか,液体の状態方程式を定性的に与える。…
※「ファン・デル・ワールスの状態方程式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by