相転移（読み）ソウテンイ

デジタル大辞泉

そう‐てんい〔サウ‐〕【相転移】

物質がある相から別の相に移ること。融解・蒸発、凝縮・凝固など。相変化。→相4

出典　小学館

日本大百科全書(ニッポニカ)

相転移
そうてんい

物質の相転移

相変化ともいう。同一の物質でも、温度や圧力の変化により物理的な性質が明確に異なる状態に変化する。異なったそれぞれの状態を相という。ある相から別の相へ転移する現象を相転移とよぶ。たとえば、1気圧で、氷（固相）を暖めると、0℃で融解して水（液相）になり、100℃で水蒸気（気相）になる。これは化学組成はH₂Oで変わらないが、物理的な性質が異なる状態であり、固相・液相・気相間の相転移である。固体でも、結晶構造が異なると異なった性質をもつので、別の相である。氷の場合八つの固相が知られている。

　他の相転移の例としては常磁性相と強磁性相（永久磁石）、常誘電相と強誘電相、合金の無秩序相と秩序相、金属の常伝導相と超伝導相、液体へリウムの常流動相と超流動相、液晶の等方相、ネマチック相、スメクチック相などがある。以上は平衡相転移とよばれ、熱平衡状態での相が温度や圧力や外場を変えたとき、別の相に変化する現象である。

　一方、非平衡相転移といわれる熱平衡でない相の転移現象もある。流体の流速が小さいときは層流であるが、大きくなると渦が生じ、さらに大きくなると乱流が生じる。流体の上層と下層との温度差が閾値(しきいち)に達すると、初めて対流が生じる。さらに温度差が大きくなると、乱流へと移行する。このような転移では、各相は熱平衡でなく、つねに外部からエネルギーを供給されている環境で生じるので、非平衡相転移という。

［小野昱郎］

気相、液相、固相の相図

圧力と温度を定めたとき、物質の気相、液相、固相のなかでどの相が安定に存在するかを示すものを相図という。図Aに水の相図が示されている。液相と気相の境界線を蒸気圧曲線、固相と液相の境界線を融解曲線、固相と気相の境界線を昇華曲線という。いずれの境界線上でも両側の相が共存しうる。これら3本の境界線が交わる点は三重点といい、3相が共存する。水ではその温度はT_t＝0.01℃、また圧力はp_t＝0.0053atmである。

　図Aで、蒸気圧曲線は右上がりになっているが、これは圧力が上昇すると水の沸騰温度が上昇し、圧力が減少すると沸騰温度が降下することを表している。家庭用の圧力釜でも沸騰温度は120℃以上になる。このとき釜内の圧力は2atm以上になっている。また、富士山山頂付近でご飯がうまく炊けないのは、気圧は0.63atmとなり、水の沸騰温度は約87℃になるためである。

　蒸気圧曲線は臨界点で終わる。水の臨界温度はT_c＝374℃、また臨界圧力はp_c＝218atmである。臨界点では水から水蒸気に移るときの気化熱は0で、また体積や密度の不連続もない。ただし、臨界点では密度のゆらぎが異常に大きくなるので、透明だった気体が白く光る。これを臨界タンパク光とよぶ。臨界温度または臨界圧力以上になると、転移に伴う異常はみられず、密度が滑らかに変化していくので、液体と気体の区別を明確につけることはできない。

　一方、融解曲線は左上がりになっており、圧力が上がると融解温度は下がる。氷にスケートの刃のような強い圧力がかかると、0℃以下でも氷が融けるのは、この理由からである。また蒸気圧曲線のような臨界点はみつかっていないので、固相と液相の区別はつねに明確である。液相と固相（結晶）の間では分子の配列の対称性が異なるので、臨界点はないと信じられている。一般の物質では融解曲線は右上がりになっており、水の場合が特別であることが知られている。

　昇華曲線は固相と気相の共存線である。ドライアイスは固体であるが、三重点の圧力は5.1atmであり、1atmでは直接炭酸ガスに転移する。氷の場合も三重点以下の圧力では、直接水蒸気に転移する。これを昇華という。

［小野昱郎］

気相、液相間の相転移

温度を一定に保ったまま、圧縮する過程での相転移を図Bで見てみよう。温度が臨界温度より低い場合、A点（気相）から出発して、圧縮していくと、B点で気相の一部が液相に転移し、気相と液相が共存する。さらに圧縮を続けると、液相はしだいに増加し、C点で全部液相に変わる。B点からC点まで、圧力は一定のままである。以後、CD間はすべて液相になるので、圧縮により急速に圧力は増加する。温度が臨界温度より高い場合、圧縮とともに滑らかに圧力が増加していくが、とくに2相に分かれることはない。

［小野昱郎］

転移の次数

相転移が生じるとき、物質の相を特徴づける熱力学状態変数の転移点付近での異常の程度により分類され、転移の次数が決められる。熱力学状態変数（以下、状態変数と略す）が転移点で不連続となるとき、一次相転移という。状態変数とは、物質の熱力学状態を指定する量で、たとえば、温度、圧力、体積、密度、内部エネルギー、自由エネルギー、エントロピーなどである。熱量、仕事量は状態変数ではない。固相、液相、気相の相変化の場合、独立な状態変数は二つであり、ほかの状態変数はこの二つによって決まる。一定量の物質では、たとえば温度と圧力を指定することにより体積、内部エネルギーなどがすべて決まった値をとる。水から水蒸気、氷から水の転移のとき、体積（密度）が不連続に変化するので、一次相転移である。このとき、蒸発熱や融解熱が必要となるので、低温相から高温相に移るとき、これらの潜熱をΔQとすれば、エントロピーの増加はΔS＝ΔQ/Tであるから、状態変数のエントロピーも不連続になる。

　転移点で状態変数は不連続ではないが、それを温度や圧力で微分した一次導関数が不連続のとき、二次相転移とよぶ。水と水蒸気の臨界点では密度は連続に変化するが、圧力の微分を含んだ圧縮率は不連続（発散）がみられるので、二次相転移である。

　磁性体では磁化も状態変数である。永久磁石となる鉄の場合、約770℃以上では、磁化が失われる。この転移温度をキュリー温度とよんでいる。永久磁石である相を強磁性相といい、磁化が失われた相を常磁性相という。図Cに示されるように、転移温度以下では状態変数の自発磁化Mは有限であり、これ以上では自発磁化は0である。磁化は転移点では0で連続であるが、折れ曲がっている。磁化の温度微分が不連続となるので、二次相転移である。また磁化率χも発散する。超伝導相と常伝導相の転移、超流動相と常流動相の転移も二次相転移である。状態変数のさらなる高次の導関数に、不連続が初めて現われるときに、高次の相転移という。

［小野昱郎］

相転移の熱統計力学理論

磁性の相転移を例にとって述べる。固体内で格子状に配列した強磁性体の原子またはイオンはそれぞれ固有の角運動量（スピン）をもち、それに付随した磁気モーメントをもっている。もともと近接したイオン間には相互作用（強磁性交換相互作用）があり、磁気モーメントが平行にそろったほうが、反平行より、エネルギー的には有利である。絶対零度ではすべての磁気モーメントが完全に平行にそろい、全体としての磁化が発生する。これが強磁性相である。温度が上がると、熱運動のため平行に並んだ磁気モーメントの向きに乱れが生じ、全体の磁化が減少する。さらにこの乱れのために、平行にとどめておくために有効な相互作用も減少し、さらに乱れが誘発される。そのためある温度まで上昇すると、急速に秩序が壊れ、磁気モーメントはランダムな向きになって、磁化は急速に0になってしまう。

　熱力学の立場で理解するには、強磁性体では磁化Mは重要な状態変数であり、これを変数としたヘルムホルツの自由エネルギーF＝U－TSを用いることが有益である。ここで、Uは内部エネルギー、Sはエントロピーである。与えられた温度TでFが最小となるような磁化が熱平衡値である。磁気モーメントの相互作用エネルギーが内部エネルギーUにとって重要である。この値は隣り合った磁気モーメントが平行になればなるほど、つまり、全体の磁化が大きいほど、Uは低くなり、逆に、モーメントの向きがランダムで、磁化が小さいほど大きくなる。分子場近似で、Uは－M²に比例する。一方、エントロピーSは磁気モーメントの向きがランダムであればあるほど大きくなる。磁化が0のとき、Sは最大となる。逆に、磁気モーメントがすべてそろっているとき、つまり磁化が最大のとき、Sは最小になる。エントロピーSは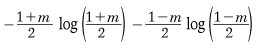

に比例する。ここでmは無次元の磁化、飽和磁化をM₀とすれば、m＝M/M₀で与えられる0≦|m|≦1の範囲である。図Dにこの近似で求めた内部エネルギーとエントロピーの磁化依存性を示した。自由エネルギーFの第2項の－TSは温度が低いときは小さいので、相互作用エネルギーUの低い状態、つまり磁化の大きい状態が有利になる。これが強磁性相が出現する理由である。温度の高いときは、第2項が重要になり、エントロピーが大きい状態、つまり磁化の小さい状態のほうが、たとえUが大きくとも、Fを大きく減少させるので有利になる。これが、磁化0の常磁性相である。その分岐点がキュリー温度である。分子場近似で、自由エネルギーを磁化の関数として図Eに示した。この方法で転移温度、磁化の温度変化、比熱の温度変化等が計算され、この転移は二次相転移であることが示された。

［小野昱郎］

イジング模型

強磁性体のもっとも簡単な理論的模型がイジング模型である。この模型では、磁気モーメントは上向きと下向きの二つの状態しかもたない。相互作用は隣接する格子間に限定され、そのエネルギーは隣接する磁気モーメントが平行のときは－J（＞0）、反平行のときは＋Jである。このような簡単な模型は統計力学に基づいて、格子が一次元で、磁気モーメントが鎖状に並んでいるとき、自由エネルギーFが求められ、絶対零度以外は磁化が現れないことが示された。二次元正方格子上では、1944年オンサーガーは厳密解を得た。それによれば、有限温度で相転移が生じ、その転移は連続相転移であること、比熱は転移点で対数発散することを示した。三次元立方格子上では、現在でも厳密解は得られていないが、相転移はあるということは確実であり、種々の近似で、転移点や熱力学的性質が求められている。

［小野昱郎］

臨界指数

強磁性の二次相転移点と液相・気相の臨界点と熱力学的性質が似ている。強磁性では、転移温度で磁化は0であるが、磁化のゆらぎは大きく、そのため磁化率は発散する。またエネルギーのゆらぎも大きく、比熱も発散することが知られている。一方、臨界点では気相と液相の密度差はなくなるが、密度のゆらぎは増大し、そのため等温圧縮率は発散する。またエネルギーのゆらぎの増大により、定圧比熱が発散する。

　温度が臨界温度（転移温度）に近づくと、熱力学量が臨界温度からの温度差のべき乗則にしたがっていることがみいだされた。磁性体ではこの温度をT_cと置くと、強磁性体の比熱は|T－T_c|^-α、磁化率は|T－T_c|^-γとなり、さらに温度が臨界点に下から近づくとき、磁化の0への近づき方が|T－T_c|^βとなるとき、この三つのべき指数を臨界指数とよび、その間には
　　α＋2β＋γ＝2
の関係があることが示唆された。このように臨界指数の間に関係式が存在し、独立な臨界指数は二つであるといわれている。平均場（分子場）近似ではα＝0、β＝1/2、γ＝1となり前記の関係式が満たされている。二次元イジング模型の厳密解はα＝0、β＝0.125、γ＝1.75となり、前記の関係式が成り立つ。三次元イジング模型の数値解析では、α＝0.12、β＝0.33、γ＝1.25となり、ほぼこの関係を満たす。臨界点での個々の臨界指数は違っていても、指数の間に成り立つ普遍的な関係式であることが示唆される。さらに相関関数に関係した他の臨界指数の導入とその関係式も提案された。これらの関係式は系の自由エネルギーが臨界点付近でスケーリングされる（一般化同次関数である）ことを仮定すれば導かれることから、臨界指数の関係式をスケーリング関係式とよんでいる。臨界指数の個々の値は相転移の特徴を表すので、これを基準に、相転移を分類することができる。もし、臨界指数が同じなら、別の相転移現象でも、同じタイプの臨界現象と分類できることにある。

［小野昱郎］

非平衡相転移

熱平衡での相転移でなく、外界から定常的にエネルギーや粒子の供給がある体系の相の変化についての例をあげる。まず、流体の流速の増加による流れの様相の変化について述べ、次に熱対流について述べる。

　一定の流速で流れている流体の中に円柱が置かれている。流速が小さいうちは流れは円柱に沿って滑らかに流れ、層状の定常流を形成している。これを層流とよぶ。流れがある程度速くなると、円柱の後方に一対の渦が発生し、流線は円柱からはがれる。この渦は流れによって運ばれていく。これをカルマン渦という。このような転移はレイノルズ数によって決まる。流速v、円柱の直径∅、動粘性係数νを用いて、レイノルズ数はRe＝v∅/νで与えられる。Reが10程度以上でカルマン渦が発生する。このような渦は一般的にみられる現象である。たとえば、強風が当たった電線が鳴る音は「アイオリスの音」（エオルス音）といい、この渦による振動である。風速が大きくなると、振動数も高くなる。さらに流速が大きくなると（Re～70）流れは不安定になり、複雑な流れとなり、ついに乱流になることが知られている（図F）。

　次にベナード対流（ベルナール対流）について述べる。流体を浅い容器に入れ、水平に置く。上面より下面の温度がわずかに高くなるように温度を制御する。流体は熱膨張により、下面の密度が上面より小さくなり、重力による対流が発生してもいいはずであるが、温度差が小さいときは対流はおこらず、熱伝導によって熱のみが流れる。これは流体の粘性によって対流の発生が抑えられているからである。上下の温度差がある程度以上になると、対流が発生する。1900年に初めて対流の発生を観測したベナードと、1916年にこれを説明したレイリーの名をとって、レイリー‐ベナード対流とよんでいる。対流は横から見て右回りと左回りの渦が対になって、等間隔に発生する。縦方向は長いロール状になる。対流の発生の閾値はレイリー数Raで決められる。

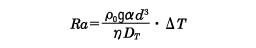
ここで、ρ₀は平均密度、gは重力加速度、αは熱膨張率、dは流体の厚さ、ηは動粘性係数、D_Tは熱拡散係数、ΔTは上下の温度差である。さらに温度差が増大すると、このパターンが複雑化し、ついにパターンが完全に壊れ、ちぎれたロールが不規則に動き回る複雑なパターンとなる。それらの動きは予測することが困難になり、流体は乱流になってしまう。これは自由度無限大のカオスとよばれている。流体が上下の温度差の増大によって、静止相から対流相へ、さらに乱流相へ転移するが、各相は熱平衡相ではなく、熱流や対流のある非平衡相である。

　大気の循環でも同様な現象が発生する。地表が強い日射で温度が上昇すると、地表付近の空気が暖められ、上層の空気より密度が小さくなる。これを逆転層という。しかし、すぐに上昇気流が発生するわけではない。温度差がさらに上がるか、何かのきっかけで、初めて上昇気流が発生することが知られている（図G）。

［小野昱郎］

地質学における相転移

鉱物間の相転移では、温度や圧力などの外的条件の変化によって結晶構造が変化することをいう。地殻を構成する鉱物では、低温低圧下で安定な紅柱(こうちゅう)石が高圧下で藍晶(らんしょう)石になり、また高温下で珪線(けいせん)石になることが知られ、変成岩の研究に重要な貢献をした。また地球深部の深さ400キロメートルから700キロメートルにかけて、主要マントル構成鉱物である橄欖(かんらん)石が圧力の増加に伴い、β(ベータ)-スピネル→γ(ガンマ)-スピネル→ペロフスカイトMgSiO₃＋マグネシオウスタイト(Mg,Fe)Oに変化する。鉱物の相転移がおこると、エントロピー、密度、弾性波速度、電気伝導度などが不連続的に変化する。地球深部の地震波速度や密度の不連続面は、マントル構成鉱物の相転移面に対応していると考えられる。

［水谷　仁］

『小口武彦著『物理学選書12　磁性体の統計理論』（1970・裳華房）』▽『H・E・スタンリー著、松野孝一郎訳『相転移と臨界現象』新装版（1987・東京図書）』▽『ヴォルフガング・ゲプハルト、ウヴェ・クライ著、好村滋洋訳『物理学叢書62　相転移と臨界現象』（1992・吉岡書店）』▽『西森秀稔著『新物理学シリーズ35　相転移・臨海現象の統計物理学』（2005・培風館）』

水の相図〔図A〕

気相・液相間のp‐V図での等温線〔図B…

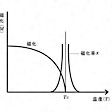
強磁性体の磁化の温度変化および磁化率〔…

内部エネルギーとエントロピーの磁化依存…

近似解法〔図E〕

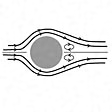
カルマン渦〔図F〕

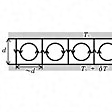
ベナード対流の断面図〔図G〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

相転移 (そうてんい)
phase transition
phase change

物質が化学的，物理的に一様であるとき，その均質な部分を相と呼ぶが，一般に物質は，例えば水（液相）が氷（固相）になったり水蒸気（気相）になったりするように，温度や圧力などによって異なる相をとる。このように，物質がある相から異なる相に移ることを相転移，または相変化という。単に転移ということもある。また相転移の起こる温度，圧力などを転移点と呼ぶ。身近な相転移として，上述の例のように気相-液相間の転移，液相-固相間の転移があるが，このほかにも強磁性体や反強磁性体が転移温度（前者の場合キュリー温度，後者ではネール温度と呼ばれる）で常磁性を示すようになる磁気転移，超伝導体が超伝導状態から常伝導状態に移る超伝導転移，液体ヘリウム（⁴Heの液体）の超流動相（液体ヘリウムⅡ）が常流動相（液体ヘリウムⅠ）に転移する超流動転移などが典型的な例である。

　過熱状態や過冷却状態のように転移点を越えても相転移が起こらないことがある。このような状態は準安定状態と呼ばれるが，相転移のうち，準安定状態を伴う相転移を第1種相転移，伴わない相転移を第2種相転移という。またこれとは別に，P.エーレンフェストは，自由エネルギーの温度や圧力に関する1階微分が転移点で有限のとびをもつとき，その相転移を一次相転移と呼び，2階微分がとびをもつとき二次相転移と呼んだ。

一次相転移

一次相転移は第1種相転移と一致する。一般に内部エネルギー，エントロピーは転移点で不連続に変わり，それに応じて気化熱，融解熱などの潜熱が伴う。気相-液相転移，液相-固相転移などがその典型的な例である。熱平衡状態として2相が存在する条件は，温度，圧力および化学ポテンシャルが両相で等しくなることであり，このことから，一次相転移では次のクラウジウス=クラペイロンの式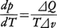，が2相の共存線（p-T図）の上で成立する。ただし，Tは絶対温度，pは圧力，⊿Qは単位質量当りの潜熱，⊿vは両相の比体積（単位質量当りの体積）の差である。例えば水と氷の間の相転移の場合，比体積をそれぞれv_w，v_iとすると，氷のほうが軽いので，⊿v＝v_w－v_i＜0であるから，dp/dT＜0となり，圧力pが大きくなるほど融解点の温度が下がる。これに対し，通常の物質では液体になると固体より密度が小さく（比体積が大きく）なり，⊿v＞0であるから，dp/dT＞0である。水と水蒸気の場合は⊿v＞0であり，圧力が下がると（例えば高い山の頂上では）沸点が下がる。一次相転移の起こる機構は，原子，分子およびスピンなどの間の相互作用によって種々さまざまであるが，熱力学的には，それぞれの相に対応する自由エネルギーを互いに比較してその低いほうの相に転移する。
→臨界状態

二次相転移

エーレンフェストによる二次相転移の定義では，液体ヘリウムの超流動転移のように，比熱が転移点で有限のとびでなく発散する第2種相転移が含まれなくなり，実情に合わない。このため現在では，さらに拡張して自由エネルギーの2階微分が転移点で有限のとびを示すか発散する場合，一般にその相転移を二次相転移という。二次相転移の例としては，超流動転移のほか，超伝導転移，磁気転移などがある。超流動転移と大部分の磁気転移では，転移点で比熱が発散し，絶対温度と比熱の関係をグラフに書くと，図1のようにギリシア文字のλに似ていることからλ転移と呼ばれる（狭義には超流動転移のみをλ転移という）。三次以上の相転移は現実には見つかっていないので，第2種相転移の大部分は二次相転移である。二次相転移は，秩序パラメーターと呼ばれる熱力学的変数（何が秩序パラメーターになるかは相転移の種類によって異なるが，例えば強磁性体の磁気転移においては磁化である）が転移点で連続的に変化するので，連続転移と呼ばれることもある。

　二次相転移は対称性の自発的破れとしてとらえることもできる。すなわち，図2に示したように，エントロピーの力と系の力学的な協力的力との競合により，転移点T_cより上側では前者が勝って無秩序状態となり，対称性の高い状態が実現する。逆に転移点より下側では後者が勝って秩序状態となり，対称性の低い状態が実現する。二次相転移を扱う一般論としては，L.D.ランダウの現象論がある。それは，自由エネルギーFを秩序パラメーターηの関数と考え，Fがηに関して，図3のようにふるまうとして相転移のようすを説明する。すなわち，T＜T_cでは，Fを極小にするηの値は二つ現れ，これが自発的な秩序パラメーターとなる。T＞T_cではFを極小にするηは0となり，無秩序状態になると解釈される。この転移点近傍では，いろいろな物理量に異常性が現れ，それらは臨界現象として，くりこみ群などを用いて詳しく研究されている。
→臨界現象
執筆者：鈴木 増雄

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

相転移【そうてんい】

物質がある一つの相から他の相へ変化すること。単に転移ともいう。融解，凝固，気化（蒸発），昇華，凝縮などは一般によく知られた例であるが，ほかに結晶状態の変化（単斜硫黄と斜方硫黄との間の転移など），鉄などでみられる強磁性体から常磁性への転移，液体ヘリウムIからIIへの転移など各種のものがある。
→関連項目ウィルソン｜キュリー温度｜潜熱｜転移点｜リー｜リチャードソン

出典　株式会社平凡社

化学辞典 第2版

相転移
ソウテンイ
phase transition

相変化ともいう．温度，圧力，組成比などの変化で，ある一つの相からほかの相へ変化することをいう．相転移には一次相転移(first order transition)と二次相転移(second order transition)とがある．気相と液相間(気化，液化)，液相と固相間(結晶化，融解)の相変化においては，体積，エントロピーなど(相の化学ポテンシャルの一次導関数)が不連続的に変化し，転移熱(潜熱)を伴い，一次の相転移とよばれている．二次相転移では，体積，エントロピーなどが連続に変化し，転移熱を伴わず，比熱，熱膨張係数，磁化率など(相の化学ポテンシャルの二次導関数)が不連続に変化する．このような二次相転移を示すものとして，合金結晶中の原子配列の規則化，強磁性体から常磁性体への転移，常伝導状態から超電導状態への転移，液体ヘリウムの超流動状態への転移などがある．

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

相転移
そうてんい
phase transition

相変化ともいう。1つの相から他の相へ移る協力現象。相転移には，エントロピーや体積などの値が両相で有限の差をもつような一次相転移と，定圧比熱や等温圧縮率の値に有限の差をもつような二次相転移とがある。一次相転移の例としては水蒸気から水，水から氷への転移などがあり，二次相転移の例としては磁性体における常磁性-強磁性転移，合金の秩序無秩序転移，液体ヘリウムの λ 点における正常流体から超流動流体への転移などがある。

出典　ブリタニカ国際大百科事典 小項目事典

知恵蔵

相転移

固体、液体、気体のような物質の状態(相)が、温度や圧力などの変化でがらりと変わること。微視の粒子世界の変容が巨視的、劇的に見える。境目の温度などを転移点という。典型例は、水が氷になったり(凝固)、氷が水になったり(融解)する現象。広く、物質の秩序が崩れて一気に無秩序になったり、無秩序から秩序が急に現れたりすることも指す。強磁性体の強磁性状態と常磁性状態、超伝導体の超伝導状態と常伝導状態の変化などがこれに当たる。宇宙がビッグバン後に冷えて1つの力が4種に分かれてきた変化も、こう呼ぶ。

(尾関章 朝日新聞記者 ／ 2007年)

出典　(株)朝日新聞出版発行「知恵蔵」

岩石学辞典

相転移

温度，圧力，外部磁場，成分比などの変数の変化によって物質が異なる相に移る現象［長倉ほか : 1998］．

出典　朝倉書店

栄養・生化学辞典

相転移

　転相ともいう．気体，液体，固体の間の変化．

出典　朝倉書店

世界大百科事典（旧版）内の相転移の言及

【超高圧】より

…　超高圧領域で圧力の絶対値を決定する際には，特別の手法が採用される。圧力定点法はその代表であり，種々の元素や化合物の圧力誘起の相転移を利用した圧力定点(表)が提唱されている。圧力定点の絶対値を決定するにあたって，もっとも信頼性の高い手法は標準物質(NaClなど)の状態方程式に準拠する超高圧X線回折法である。…

【臨界現象】より

…一般に二次相転移点近傍でゆらぎが非常に大きくなり，物理量に異常性が現れる現象をいう。例えば気相‐液相の臨界点では，密度が不安定になって密度の大きなゆらぎが現れ，その結果，光の散乱が異常に大きくなる。…

※「相転移」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」