ドモアブル（読み）どもあぶる（英語表記）Abraham de Moivre

精選版 日本国語大辞典

ド‐モアブル

1. ( Abraham de Moivre アブラアム━ ) フランスの数学者。一八歳のときロンドンに移住。王立協会会員。複素数に関する「ド‐モアブルの定理」を発見。（一六六七‐一七五四）

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

ド・モアブル
どもあぶる
Abraham de Moivre
（1667―1754）

イギリスの数学者。フランスのシャンパーニュ地方のビトリで生まれる。1685年「ナントの勅令」の廃止により、カトリック教徒以外は弾圧されることになり、ド・モアブルの両親は逃亡を決意しロンドンへ移住した。彼の18歳のときであった。ロンドン移住以前にどのような教育を受けていたかは明らかでないが、移住後は当初から数学を教えて家計を助けた。

　ニュートンやハリーの紹介で、王立協会で論文を発表できるようになり、1697年にはこの協会の会員に選ばれた。晩年は、眠る時間がしだいに長くなるという奇病に取りつかれ、最後には24時間を眠り続けたまま生涯を閉じた。

　確率に関する論文「偶然の原理」（1716）は、確率論における重要なものであるが、彼を語るとき、1730年に公刊された「級数と求積とに関する解析学の諸問題」と題する論文は見逃してはならない。この第1章に「半径1の円の弧AとBの余弦が、それぞれl、xであり、A＝nBという関係があると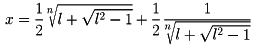

が成り立つ」という定理がある。現代の記号で表すとl＝cosAであるから、l²－1＝－sin²Aである。ゆえに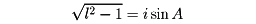

となるので、上の式は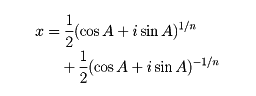

となるので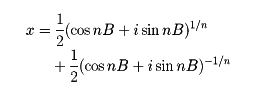

を得る。また、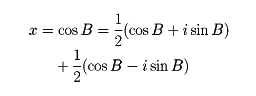

であるから
　(cosB＋isinB)ⁿ＝cosnB＋isinnB
　(cosB＋isinB)^－n＝cosnB－isinnB
を得る。これが「ド・モアブルの定理」といわれているものであり、数学の歴史において輝かしい光を放っている。

［小堀　憲］

[参照項目] | ド・モアブルの定理 | ニュートン | ハリー

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

ド・モアブル
Abraham de Moivre
生没年：1667-1754

フランスの数学者。はじめはおもに古典文学の教育をうけたが，まもなく数学の才能を発揮し，C.ホイヘンスの偶然ゲームの理論に影響されて，数学，とくに確率論への道を歩むこととなった。ソルボンヌで数学，物理学を学んだ後，宗教上の理由で1688年ロンドンに移住した。しばらくは不遇であったが，97年にはローヤル・ソサエティのフェローとなった。この間I.ニュートンとの親交は，数学者として大成するのに大いに役だった。彼は，今日スターリングの公式と呼ばれるnが大きいときn！の近似値を与える公式を，定数を除いて確定し，さらに，ベルヌーイ試行，すなわち二項分布が現れる場合の中心極限定理を導いた。これは今日ド・モアブル=ラプラスの定理と呼ばれている。ド・モアブルの定理（公式）と呼ばれる式は，複素数と三角関数を結ぶ基本公式として有名である。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

ド・モアブル
De Moivre， Abraham

[生]1667.5.26. シャンパーニュ，ビトリ
[没]1754.11.27. ロンドン
イギリスの数学者。元来はフランス人であるが，1685年のナントの勅令の廃止により，両親とともにイギリスに逃れ，ロンドンに住む。ニュートンと親交を結び，97年にロイヤル・ソサエティ会員になる。ニュートンとライプニッツの間の微積分学の優先権争いを裁くための委員会の委員に指命される。論文の大部分はロイヤル・ソサエティの機関誌"Philosophical Transactions"に載った。彼がこの雑誌に発表した最初の論文は，賭けの分け前に関するもので (1711) ，確率についての研究は『偶然論』 (18) にまとめられている。もう1つの重要な著作は『解析概論』 (30) である。この本の第1章には有名なド・モアブルの公式が書かれている。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

ド・モアブル

フランスの数学者。ユグノーであるため圧迫を受け1688年から英国に移住。ニュートン，ハリーと親交あり，1697年王立協会会員。三角法でド・モアブルの定理を，確率で正規分布曲線を発見。

出典　株式会社平凡社