フェルマーの原理（読み）ふぇるまーのげんり（英語表記）Fermat's principle

日本大百科全書(ニッポニカ)

フェルマーの原理
ふぇるまーのげんり
Fermat's principle

幾何光学の基礎になる原理。「2点間を進む光の径路は、幾何学的に可能な径路のなかで所要時間が極値をとるもの」と表現される。これに基づき、媒質境界での光線の反射・屈折や、光の波長の程度ではほとんど屈折率が変わらないような不均一媒質での光の径路を決めることができる。1661年にフランスの数学者フェルマーが定式化し、屈折の法則を導出した。均一媒質中での光の直進は、特別な場合として得られる（以下で光速という場合、波長と振動数の積を意味する）。

　いま光速v_A、v_Bで光が進む媒質A、Bが平面で接するとき、光がP→R→Qと進む所要時間tは、図の(1)より

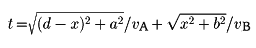
である。tがxの変化に対して極値をとる条件から、v_A/v_B＝sinθ/sin∅が得られ、屈折の法則になる。この式は、それぞれの媒質の絶対屈折率n_A＝c/v_A、n_B＝c/v_B（cは真空中での光速）を用いた形n_B/n_A＝sinθ/sin∅（スネルの関係、スネルの法則）にも表される。反射の法則については図の(2)から、実際の径路P→R→Qが最短時間になることがわかる。2媒質が平面で接するときtの極値は最小値になるが、一般の曲面の場合に極大値になることも、また極大にも極小にもならないこともある（図の(3)）。しかしながら、原理の表現を、「固定された2点間P、Qを光が進む所要時間は、途中の径路の任意の微小変化に対し不変、すなわち所要時間の径路に関する変分が0である」として、その内容を変分原理

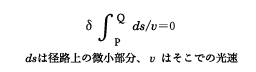
として表せば、曲面での屈折・反射や不均一媒質中での光の径路を含め幾何光学の内容を与える基本式となる（1/vのかわりに径路上の絶対屈折率n＝c/vを用いてもよい）。物質粒子のもつ波動性を用いて、エネルギー一定の質点の運動を決める力学での最小作用の原理を書き直すと、この変分原理に対応した関係が得られる。

［藤井寛治］

[参照項目] | フェルマー

フェルマーの原理〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

フェルマーの原理 (フェルマーのげんり)
Fermat's principle

光が，その波長より広い空間でどのように伝わるかを述べたもの。P.deフェルマーによってまとめられたもので，光が点P₁からP₂へ進むときの実際の経路は，他の仮想的な経路に比べて，通過に要する時間が最短となる経路であると表現される。光の波長が0の極限で正確であり，波長が有限の場合も，レンズの焦点のように光が集まるところおよび影との境のように光の振幅が急激に変わるところを除いて正しい結果を与える。フェルマーの原理を基に光の直進，反射および屈折の法則が導出される。光の経路sに沿った屈折率nの積分を光路程，または光学距離optical distanceというが，これは，光がその経路を通過するのに要する時間と真空中の光速度との積に等しい。したがって，フェルマーの原理は，光は光路程が最小であるような経路を通る，すなわち，

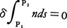
といい換えることができる。フェルマーの原理は，実際の経路を仮想的な経路と比較して，ある物理量が最小となることを主張する変分原理の一つであり，力学における最小作用の原理に相当するものである。
→最小作用の原理
執筆者：三須 明

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

フェルマーの原理【フェルマーのげんり】

一点から出た光線が何回か反射，屈折をしたのち他の一点に達するとき，光線のいろいろな通り道を考え，それぞれについて経路の各部分の長さにその場所の屈折率を掛けて加え合わせたもの（光学距離）を計算してみると，実際に光線が通る道に対してはそれが極小になるという原理。これは〈光線は極小の時間で到達できるような経路をとる〉ともいいかえられる。フェルマーが1662年に発表。
→関連項目光線｜フェルマーの定理｜変分学

出典　株式会社平凡社

法則の辞典

フェルマーの原理【Fermat principle】

光線などの電磁波が2点を伝播するとき，所要時間が最短になる経路を辿る，という原理．最小時間の原理＊ともいう．

出典　朝倉書店

世界大百科事典（旧版）内のフェルマーの原理の言及

【最小作用の原理】より

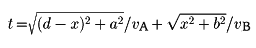
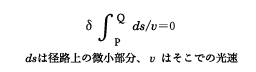
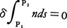
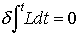…そしてTが正値であることから，作用積分の停留値，はこの場合実際に最小値であることがわかる(一般のハミルトン原理では，作用積分の停留条件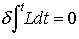は最小値を与えるとは限らない)。モーペルテュイは，彼の最小作用の原理を幾何光学における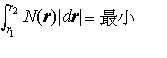フェルマーの原理との類推で考えついたものである。すなわち，波動性が無視される光線としての光の進行路は，屈折率N(r)の媒質中で(rは位置ベクトル)，すなわちr₁，r₂を結ぶあらゆる経路のうちこの積分を最小にするものによって定められる。…

※「フェルマーの原理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」