最小作用の原理（読み）サイショウサヨウノゲンリ（英語表記）principle of least action

デジタル大辞泉

さいしょうさよう‐の‐げんり〔サイセウサヨウ‐〕【最小作用の原理】

物理学における基本原理の一つ。ある系における物体の運動は、作用量という物理量を最小とする経路に沿うというもの。ラグランジュが考案した変分法を適用することによって、物体の運動を記述する運動方程式が得られる。最小作用の法則。

出典　小学館

改訂新版　世界大百科事典

最小作用の原理 (さいしょうさようのげんり)
principle of least action

質点はその作用積分が各時刻において最小となるような軌道を描くという力学原理。解析力学の枠組みにおけるもっとも一般的な形に述べられる運動法則，すなわちハミルトンの原理が現れる以前，直観的に運動法則を述べる試みとして，1744年P.L.M.deモーペルテュイによって最初に提出された。ここで作用積分とは，質点の運動量p（t）をその描く軌道q（t）に沿って積分する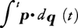，のことを意味していた（tは時間）。のちのハミルトンの原理からみてモーペルテュイの主張が正しいのは，質点のもつハミルトン関数Hがp（t），q（t）以外に直接tに依存しない形式の場合，すなわちHが一定値E（運動エネルギーTと位置エネルギーUの和），言い換えれば軌道がすべてこのような等エネルギー面上にある場合である。実際，このとき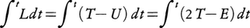となり（L＝T－U，H＝T＋Uはそれぞれラグランジュ関数とハミルトン関数），したがって運動を決める変分原理は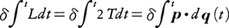，のように，モーペルテュイの形式とハミルトンの形式とが一致する。そしてTが正値であることから，作用積分の停留値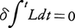，はこの場合実際に最小値であることがわかる（一般のハミルトン原理では，作用積分の停留条件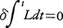は最小値を与えるとは限らない）。モーペルテュイは，彼の最小作用の原理を幾何光学におけるフェルマーの原理との類推で考えついたものである。すなわち，波動性が無視される光線としての光の進行路は，屈折率N（r）の媒質中で（rは位置ベクトル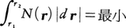），すなわちr₁，r₂を結ぶあらゆる経路のうちこの積分を最小にするものによって定められる。これに対比してモーペルテュイの原理は，質点の質量をm，速度をv（r）として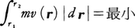，という形式に書かれることから，光線の進行路を決める法則と質点の軌道を決める法則との対応は明らかであろう。しかし，ここで注意すべきことは，媒質中の光の速さV（p）は真空中の光速cによりV（r）＝c/N（r）で表されるので，両原理の対応関係はよりくわしく，

ということになる。すなわち前者では速度因子が分母に現れる点が異なっているが，ド・ブロイは光線を描く粒子，すなわち光子に対して，運動量を，エネルギーE＝hν（hはプランク定数，νは振動数）からhν/V（r）で定義するならば，光子に対するフェルマーの原理がモーペルテュイの原理とまったく一致することに気づいて，ド・ブロイの関係式の名で呼ばれるE＝hν，p＝hν/cに基づく波動力学の考えに到達した。すなわち，幾何光学は波動論に従う光波の波長0の極限とみられることから，古典力学に従う質点に対しても同様な位置を占める波動理論が成立すると考えるわけで，すべての物質構成粒子に対し波，すなわち物質波が伴うと予想した。このことは歴史的に，最小作用の原理が古典力学から量子力学への橋渡し，とくに電子波の実証という重要な事実の動機となったことを意味している。
→ハミルトンの原理
執筆者：長谷川 洋

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

最小作用の原理
さいしょうさようのげんり
principle of least action

物体の運動は作用（または作用積分）という量が最小になるように軌道（時間的移動経路）が決まるという原理。物理学の基礎原理の一つである。1744年にモーペルチュイにより提案されたことから、モーペルチュイの最小作用の原理ともよぶ。束縛条件が時間によらず、位置エネルギーUが速度や時間に依存しない場合、Tを運動エネルギーとすると、2Tを時刻t₁からt₂まで積分したものを作用積分とよび、この変分が0になるように運動の軌道が決まるという原理である。式で表すと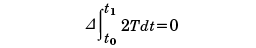

となる。のちにオイラー、ハミルトンにより洗練され、L＝T－Uというラグランジアンの変分が0になるように運動が決まるという、ハミルトンの原理（ハミルトンの最小作用の原理）に進化した。この原理は解析力学のみならず、マクスウェルの電磁気学、アインシュタインの相対性理論、量子力学などの研究において、指導指針となっている。この原理の光学版がフェルマーの原理である。

［山本将史　2022年2月18日］

[参照項目] | 位置エネルギー | 運動エネルギー | オイラー | ハミルトン | ハミルトンの原理 | フェルマーの原理 | マクスウェル | モーペルチュイ

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

最小作用の原理
さいしょうさようのげんり
principle of least action

力学における変分原理の1種で，時刻 t₁ と t₂ の間の実際の運動経路は，同じ両端点を通り，同じ全エネルギーをもつ経路のなかで作用量が最小となるものであるという原理。1個の質点の運動に対して 1747年 P.L.M.モーペルチュイが提唱した原理を一般化したもので，さらに一般化したものにハミルトンの原理がある。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

最小作用の原理【principle of least action】

「最小作用の法則」のページをご覧ください。

出典　朝倉書店