ベッセル関数（読み）ベッセルカンスウ（その他表記）Bessel function

デジタル大辞泉

ベッセル‐かんすう〔‐クワンスウ〕【ベッセル関数】

ベッセルの微分方程式の解となる関数。円柱座標または極座標で惑星軌道の時間変化を解く際などに現れる二階の微分方程式の解を指し、軸対称性の運動や波の記述に用いられる。第一種円柱関数。

出典　小学館

改訂新版　世界大百科事典

ベッセル関数 (ベッセルかんすう)
Bessel function

νを任意の複素数とするとき，2階の線形常微分方程式，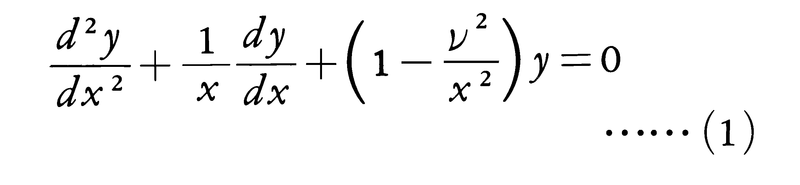

をベッセルの微分方程式という。νが整数（0，±1，±2，……）でないときは，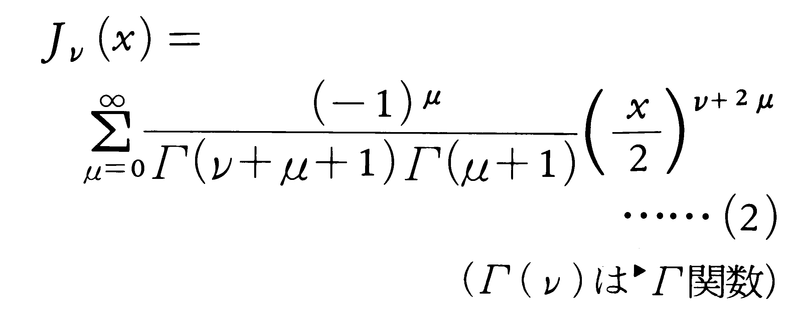

は0＜｜x｜＜∞で収束し，（1）の解となる。

これを第1種ベッセル関数または円柱関数という。ここでJ_ν（x）とJ_-ν（x）とは一次独立である。νが0または正の整数nのときも（2）は（1）の解であり，（2）の右辺の級数は｜x｜＜∞で収束する。この場合，（2）のνを－νでおきかえてから形式的にν→nとして，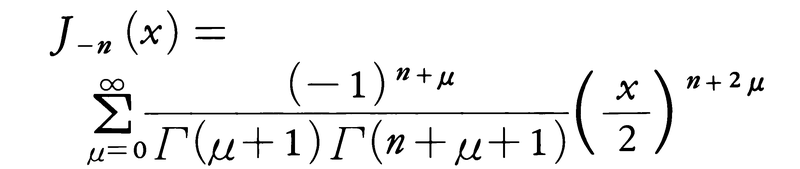

と定義するが，J_n（x）＝（－1）ⁿJ_-n（x）なる関係があるから，J_n（x）とJ_-n（x）とは一次独立でない。νを再び任意の複素数として，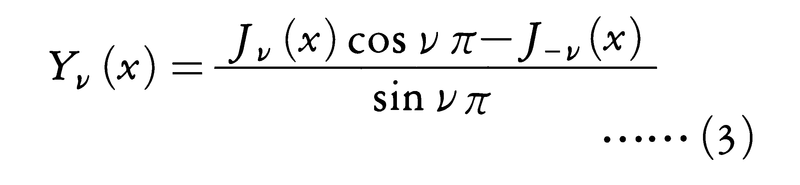

と定義する。ただし，νが整数nのときはこれは不定形（0/0の形）になるので，形式的にν→nとしたときの極限値で定義すると，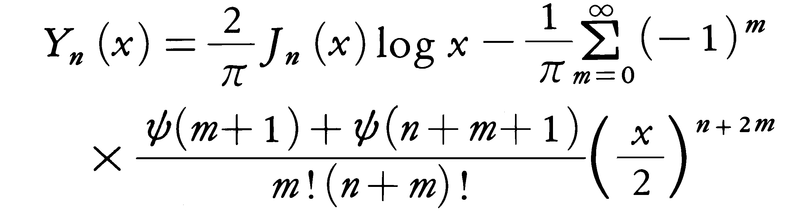



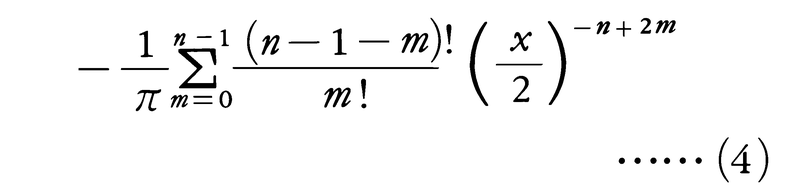
が得られる。ただし，ψ（λ）＝Γ′（λ）/Γ（λ）である。（4）をハンケルH.Hankelの公式という。任意の複素数ν（整数でもよい）に対してJ_ν（x）とY_ν（x）とは（1）の一次独立な解であって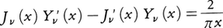，という関係式を満たす。これをロンメルLommelの公式という。Y_ν（x）はN_ν（x）とも書き，第2種ベッセル関数またはノイマンC.G.Neumann関数と呼ばれる。また，

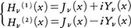を第3種ベッセル関数またはハンケル関数という。ベッセル関数は歴史的には惑星の運動に関するケプラーの方程式を解くために考えられ，さらにF.W.ベッセルによって組織的に研究されたが，その後いろいろの問題に現れ，応用上重要な地位をしめるに至った。例えば，ヘルムホルツの方程式と呼ばれる数理物理学で重要な方程式Δu＋k²u＝0（Δ＝∂²/∂x²＋∂²/∂y²）において独立変数を直交座標（x，y）から極座標（r，θ）に変換すると，この方程式はベッセル関数J_n（r）を使ってJ_n（kr）cosnθ，J_n（kr）sinnθ（n＝0，1，2，……）と表される解をもつ。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

ベッセル関数
ベッセルかんすう
Bessel function

F.ベッセルの微分方程式 z²y''＋zy'＋(z²－p²)y＝0 の解として現れる
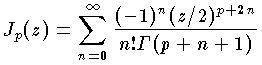で定義される関数。ラプラス作用素の軸方向を表わすので，応用数学において非常に重要な役割を演じる関数である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

ベッセル関数【ベッセルかんすう】

広義には，ベッセルの微分方程式（式１）の解をいい，狭義にはその一つ（式２）で定義される関数J(/n)（x）をいう。ここでΓ（n＋r＋１）はガンマ関数で，（式３）n＋rが整数ならΓ（n＋r＋１）＝（n＋r）！。ベッセルの微分方程式は物理学，工学で応用が広いため，ベッセル関数も詳しく数値計算され数表に作られている。

出典　株式会社平凡社