精選版 日本国語大辞典 「ベルヌーイの定理」の意味・読み・例文・類語
ベルヌーイ の 定理(ていり)
最新 地学事典 「ベルヌーイの定理」の解説
ベルヌーイのていり
ベルヌーイの定理
Bernoulli’s theorem
スイスの物理学者Daniel Bernoulli(1700.2.8~82.3.17)による定理。完全流体の定常流の状態において,流線に沿ったエネルギー保存則を表すもので,流速をv, 圧力をp, 高さをz, 流体密度をρ,重力加速度を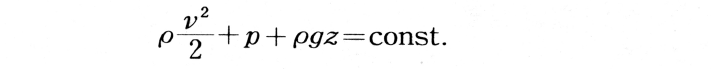
これをベルヌーイの式(Bernoulli’s equation)という。左辺の第1項は単位質量のもつ速度のエネルギー,第2項は圧力のエネルギー,第3項は位置のエネルギーで,これら3種のエネルギーの和は一つの流線に沿って一定であることを示している。
執筆者:村越 直美
出典 平凡社「最新 地学事典」最新 地学事典について 情報
日本大百科全書(ニッポニカ) 「ベルヌーイの定理」の意味・わかりやすい解説
ベルヌーイの定理
べるぬーいのていり
Bernoulli's theorem
粘性が無視できる完全流体で、その密度が流れに沿って変化せず(水はこの典型である)、かつ定常的に流れている場合、流線に沿って関係式
H=p+(1/2)ρv2+ρΩ
が成り立つという定理。スイスのD・ベルヌーイが1738年に発表した。ここに、pは静圧、ρは流体の密度、vは流速である。Ωは、流体に働く力Fのポテンシャルである。地球上の重力の場合、ΩはΩ=gzと表される。gは重力加速度、zはある基準点から測った流体の高さを示す。ベルヌーイの定理は運動方程式を積分して得られるもので、流線上で流体のエネルギーHが保存されることを示している。Hの右辺第1項は圧力によって蓄えられる内部エネルギー、第2項は運動エネルギー、第3項は位置エネルギーを表している。ベルヌーイの定理は、いろいろな流体現象の説明や、流量や流速の測定器に応用されている。
ベルヌーイの定理は、より一般的な流体について拡張される。流体の密度ρが圧力pの関数で表される場合は、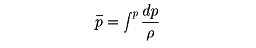
を用いてH=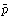 +(1/2)v2+Ωが一定となる(バロトロピー流という)。また、流れが定常的ではないが渦なしの場合、流れの速度vは速度ポテンシャルΦで表される。この場合、
+(1/2)v2+Ωが一定となる(バロトロピー流という)。また、流れが定常的ではないが渦なしの場合、流れの速度vは速度ポテンシャルΦで表される。この場合、
は渦なしの流れ全領域にわたって保存される。これを圧力方程式または一般化したベルヌーイの定理という。
[池内 了]
改訂新版 世界大百科事典 「ベルヌーイの定理」の意味・わかりやすい解説
ベルヌーイの定理 (ベルヌーイのていり)
Bernoulli's theorem
定常で粘性を無視できる流れの中での圧力,流速(運動エネルギー),位置エネルギーの間の関係を表す定理。その原型はD.ベルヌーイによって1738年に提出された。流体の流速をq=|v|,密度をρ,圧力をp,重力の加速度をg,ある任意の水平面からの高さをzとすれば,密度ρが一定という条件の下に,一つの流線に沿って,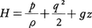 が一定というものである。この定理はρがpの1価関数(バロトロピック流体)で,外力がポテンシャルΩをもつ保存力であるときにも一般化され,
が一定というものである。この定理はρがpの1価関数(バロトロピック流体)で,外力がポテンシャルΩをもつ保存力であるときにも一般化され,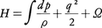 が流線に沿って,また渦分布があるときには渦線に沿っても一定となる。ここで,
が流線に沿って,また渦分布があるときには渦線に沿っても一定となる。ここで,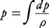 は圧力関数と呼ばれ,密度一定の流れではp/ρ,等エントロピーの流れではエンタルピーとなる。また流線と渦線で作られ,そのうえでHが一定である面はベルヌーイ面と呼ばれる。Hの値は一般には流線ごとに異なるが,渦のない定常流ではいたるところでHが一定であり,また,非定常流でも渦なしで速度ポテンシャルΦ(こう配gradΦが速度vを与える)が存在すれば,圧力方程式(一般化されたベルヌーイの定理ともいう)
は圧力関数と呼ばれ,密度一定の流れではp/ρ,等エントロピーの流れではエンタルピーとなる。また流線と渦線で作られ,そのうえでHが一定である面はベルヌーイ面と呼ばれる。Hの値は一般には流線ごとに異なるが,渦のない定常流ではいたるところでHが一定であり,また,非定常流でも渦なしで速度ポテンシャルΦ(こう配gradΦが速度vを与える)が存在すれば,圧力方程式(一般化されたベルヌーイの定理ともいう)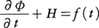 が流れのいたるところで成立する(f(t)は時間tの任意関数)。
が流れのいたるところで成立する(f(t)は時間tの任意関数)。
ベルヌーイの定理は,いわば圧力のなす仕事をとり入れた,単位質量の流体のエネルギー保存則であり,粘性のない完全流体に対してのみ成立するものである。粘性の影響の小さい流れでは近似的に成立するが,一般には粘性散逸によって流線に沿ってHの損失があることや,側壁からの加熱などの影響をとり入れて実用に供することができる。
執筆者:橋本 英典
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
法則の辞典 「ベルヌーイの定理」の解説
ベルヌーイの定理【Bernoulli principle】
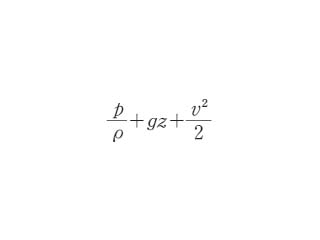
は一定となる.ここで p は流体の圧力,ρ は流体の密度,v は流体の速度,z は鉛直高さ,&scriptg; は重力加速度である.これは言葉で表すと「定常的に流れている流体の任意の点において,圧力水頭,速度水頭および高さの和は一定である」ということになる.ベルヌーイの法則*とも呼ばれている.
実際にダムから傾斜水路で水を流すとき,基準面に対する高さ(位置水頭 H1)z,その点の流速 v,水の密度を γ として,圧力水頭 H2=p/γ=p/&scriptg;γ [m],速度水頭H3=v2/2&scriptg; [m]としたとき,
H1+H2+H3=H0
(一定,ダムの水面の高さ)
書き換えると
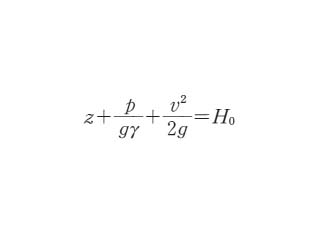
となる.
ブリタニカ国際大百科事典 小項目事典 「ベルヌーイの定理」の意味・わかりやすい解説
ベルヌーイの定理
ベルヌーイのていり
Bernoulli's theorem
ベルヌーイの定理
ベルヌーイのていり
Bernoulli's theorem
 である。 J.ベルヌーイ (1世) が定式化した。
である。 J.ベルヌーイ (1世) が定式化した。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「ベルヌーイの定理」の意味・わかりやすい解説
ベルヌーイの定理【ベルヌーイのていり】
→関連項目ピトー管|ベンチュリ管|流量計
出典 株式会社平凡社百科事典マイペディアについて 情報
化学辞典 第2版 「ベルヌーイの定理」の解説
ベルヌーイの定理
ベルヌーイノテイリ
Bernoulli theorem
非圧縮性で粘性のない理想流体に対して,一つの流管の任意の2断面における,エネルギー保存則を示した関係式をいう.一般に,流管中の任意断面での流速u,重力換算係数 gc,重力加速度g,基準面からの高さz,圧力p,流体密度ρとすると,
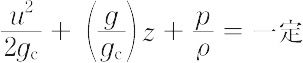
となる.これがベルヌーイの定理で,第1項を速度ヘッド,第2項を位置ヘッド,第3項を圧力ヘッドという.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
パラグライダー用語辞典 「ベルヌーイの定理」の解説
ベルヌーイの定理
出典 パラグライダー用語辞典について 情報
冬に 4日間暖かい日が続くと 3日間寒い日が続き,また暖かい日が訪れるというように,7日の周期で寒暖が繰り返されることをいう。朝鮮半島や中国北東部の冬に典型的な気象現象で,日本でもみられる。冬のシベリ...

