翻訳|entropy
精選版 日本国語大辞典 「エントロピー」の意味・読み・例文・類語
エントロピー
- 〘 名詞 〙 ( [英語] entropy ) 熱量と温度に関しての物質系の状態を表わす熱力学的量の一つ。考察する系内で、温度がどの程度に区分されているか、区分のない一様な無秩序に近いかを測る尺度。無秩序性の尺度としても拡張されて、情報理論でも利用される。→ねつりきがく(熱力学)の法則。〔物理学術語和英仏独対訳字書(1888)〕
日本大百科全書(ニッポニカ) 「エントロピー」の意味・わかりやすい解説
エントロピー
えんとろぴー
entropy
熱現象に特有な不可逆性(非可逆性ともいう)を数量的に表現するために導入された量。エントロピーという名はクラウジウスが1865年に与えた。絶対温度Tの物体が熱量Qを受けたとき、物体のエントロピーはQ/Tだけ増し、熱量Q'を放出するときエントロピーはQ'/Tだけ減少すると定める。物体が熱平衡状態にあるということは、温度や圧力や体積が指定できるということであるが、一つの熱平衡状態Aから別の熱平衡状態Bへ変わったときの物体のエントロピー変化は、AからBへきわめてゆっくり変化させていく過程を考えて、その途中で出入する熱量をそのときどきの温度で割ったものの代数和として計算する。変化が「ゆっくり」でないと、場所によって不均一を生じ物体の温度が定められないからである。
[小出昭一郎]
熱伝導によるエントロピーの増加
不可逆変化の代表的なものは熱伝導で、高温物体と低温物体を接触させれば熱はひとりでに前者から後者に流れ、温度が一様になると変化がやんで熱平衡になるが、逆はおこらない。いま、2物体が隔離されて異なる温度にある状態をA、接触後に到達する熱平衡状態をBとする。変化A→Bを「ゆっくり」行うため、両物体を隔離したまま少しずつ熱を高温物体から低温物体へ移す。しだいになくなるにしても、とにかく温度差は存在するから、途中でqだけの熱を移すときに高温物体の失うエントロピーq/T1よりも低温物体のもらうエントロピーq/T2のほうが大きい。したがってこの操作を繰り返してA→Bにしたとき、両物体のもつエントロピーの合計は増加していることになる。
[小出昭一郎]
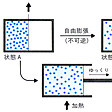
気体の自由膨張によるエントロピー増加
器を二つに仕切って、その一方に気体を入れ、他方を真空にしておく(状態A)。仕切り板を急に引き抜くと気体は器全体に広がる(状態B)。このとき気体の体積は2倍になるが、外部と仕事のやりとりはないので気体のもつエネルギーは不変で、温度もほとんど変化しない。これを自由膨張という。ところで、この変化に際してのエントロピー変化を計算するために、変化A→Bを「ゆっくり」行う必要がある。仕切り板を徐々に後退させればよいが、そうすると気体は仕切り板を押して仕事をするのでエネルギーを失い温度が下がる。そこで自由膨張と同じ結果Bにするには、仕切り板を後退させながら絶えず少しずつ加熱しなければならない。加熱をすればエントロピーが増すから、B状態の気体はA状態よりもよけいにエントロピーをもつことになる。これが自由膨張におけるエントロピー変化を示すことになる()。
[小出昭一郎]
不可逆変化とエントロピーの増大
これらの例が示すエントロピーの増加は、どんな不可逆変化の場合でも一般的におこると考えられるのでエントロピー増大の原理といわれる。熱平衡状態は、ある系の内部のエントロピーがもっとも大きくなった状態をさす(エントロピー極大の原理)。いまみた例を一般化すれば、熱エネルギーや気体分子が一方に局在した状態Aから、拡散して全体に一様に広がった状態Bへ向かうのが、不可逆変化の向きである。固体や液体の気化(蒸発)の場合も同様で、気体になることで分子の運動範囲は著しく広がる。このとき増すエントロピーは気化熱によって与えられる。固体が液体になるときには、融解熱を融解点の絶対温度で割った量だけエントロピーは増大するが、これは、固体の結晶をつくっているときには、つり合いの位置に束縛されていた分子が、もっと広い範囲にさまよい出て不規則に動き回るようになることと関連している。
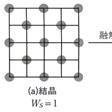
この融解という現象を簡単化したモデルで調べるために、のような碁盤状のものを考え、石を(a)のように規則正しく並べた状態が固体の結晶を表すとし、(b)のように25の升目のどこにでもかってに置いてよい不規則な状態が液体を表すとしよう。順列・組合せの考え方を適用すれば、固体の状態では並べ方は1通りしかないが、液体のときには25から13を選ぶ組合せの数だけの並べ方が存在する。つまり、固体という規則的な秩序のある状態から液体という無秩序状態に変わると、「場合の数」が急増する。きちんと整頓(せいとん)した状態というのは、可能な多くの場合のうちのごく限られた特殊の場合にすぎないからである。
[小出昭一郎]
エントロピーのミクロな定義
このようなことから、エントロピーのミクロな意味が推察できる。巨視的にみて静止している液体も、微視的にみれば異なるいろいろな状態の一つからほかへとめまぐるしく移り変わっている運動状態にある。つまり、マクロにみて一つの状態も、その裏にミクロの莫大(ばくだい)な数(Wとする)の異なる状態が隠れている。このWの数え方はむずかしく、は極度に簡単化した場合である。正しくは、分子の速度を考えに入れ、量子力学を適用する必要がある。とにかくこうしてWを決めた場合に、これをそのマクロな状態の熱力学的重率という。このWの自然対数をとり、それにボルツマン定数kを掛けたものklogeWが、そのマクロの状態におけるエントロピーに等しいことが証明されている。そうすると、エントロピーが増えるということは、Wが小さい状態から大きい状態へ変わるということである。で変化A→Bによって気体の体積が2倍になるとき、分子の速度分布は変わらないので、位置に関する可能性だけが増す。1個の分子ごとにそれは2倍になるから、分子がN個あれば全体で2N倍になる。つまりA→Bという変化でWは2N倍になるのである。したがって、エントロピーはkloge2N=Nkloge2だけ増すことになる。なお、エントロピーの概念のミクロな意味を明確化するのに多大の貢献をしたボルツマンの墓はオーストリアのウィーンにあるが、そこには、エントロピーSをミクロに定義する式S=klogWが刻んである。
[小出昭一郎]
混合のエントロピー
水とアルコールを混ぜたとすると、水の分子もアルコールの分子も混合前よりは広い範囲を動き回ることになるので、エントロピーは増加する。このとき増加するエントロピーを混合のエントロピーという。
[小出昭一郎]
熱機関の効率とエントロピー
熱を仕事や電力に変える熱機関や発電機では、作業物質として使う気体などに熱を加えて高温高圧で膨張させ、大きな仕事を取り出す。そのあと作業物質を元に戻すために圧力を下げるので冷却が必要になる。この過程で、高温の熱源(たとえば原子炉を考え、その温度をT1とする)が作業物質に与える熱量をQとすると、エネルギー保存則により、これから外部にする仕事W'を引いた残りQ-W'(これをQ'とする)が廃熱として冷却水など(温度をT2とする)に放出される。このとき、熱源や冷却水まで含めた全系のエントロピーは、増えることはあっても減ることはないから、冷却水の得たエントロピーQ'/T2のほうが、熱源の失ったエントロピーQ/T1より大きいはずである。その差は、熱の移動や蒸気の膨張などのときに増えたエントロピーであり、これをまったくなくすることは実際上不可能である。そうすると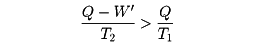
から容易に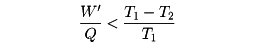
という関係が得られる。W'/Qは、加えた熱のうち、仕事や電力として使えるものの割合で効率とよばれる。この式から、熱を仕事に変えるときの効率には、熱源と冷却系の温度で決まる上限が存在することがわかる。T2をなるべく小さくすればよさそうにみえるが、低温をつくるためには別のエネルギー源、たとえば電力などが必要であり、T1を高くすることも耐熱材料などの関係で限界がある。
[小出昭一郎]
熱の利用とエントロピー
仕事を熱に変えるのは容易だが、逆は容易ではない。熱を仕事に変えるには効率に限界があるし、廃熱が不可避である。効率の式が示すように、熱は温度差がないと仕事に転換できない。温度差をつくりだすには仕事が必要である。したがって、温度差を利用せず、熱が拡散していくのを放置することは、省エネルギーの観点からは非常にもったいないことといえる。物質もエネルギーも不生不滅である(無から有を生じることはない)から、生産活動といっても、つくっているのはエントロピーだけといえる。煤煙(ばいえん)を吐き出したり汚物を川へ流せば、拡散や混合でエントロピーが増える。その意味でエントロピーはごみのように好ましくない。公害や環境問題はエントロピー増加と深く関連している。なるべくエントロピーを増やさないよう、エネルギーをむだな廃熱にしないように気をつけることが必要となる。地球は太陽から平均して1平方メートル当り222ワットのエネルギーをエントロピーとともに受け取っている。また、赤外線放射の形でほぼ同量のエネルギーを、受け取ったときより多量のエントロピーといっしょに、宇宙空間へ放出している。太陽光を集めて高温をつくりだせば、エントロピーを低く抑えられ、温度差を利用して仕事が取り出せる。これが太陽エネルギーの利用である。生命体をその系のなかだけでみるならば、生物は、エントロピー増大の原理に逆らっているようにみえる。つまり、食物を摂取して体内に秩序を取り入れることによって、体内のエントロピーを減少させている。しかし、生物は活動でできる余分のエントロピーを排泄物(はいせつぶつ)に含ませて外界に捨てることで、その微妙な秩序(生命)を保ち続けていると考えることができる。地球でも生体でも、外部から遮断された閉じた系ならエントロピーが増す一方であるが、いま述べたような開いた系としてエントロピーを捨てることで秩序を保っていると考えられる。
[小出昭一郎]
情報とエントロピー
文字や記号を一定の秩序で配列すれば情報が伝わるが、無秩序な配列では情報が失われる。エントロピーは秩序の度合いに関連した量なので、情報理論でも使われる。ただし単位の桁(けた)がまったく違うし、熱のやりとりとも直接の関係はない。
[小出昭一郎]
『小出昭一郎著『物理学One Point 1 エントロピー』(1979・共立出版)』▽『小出昭一郎・安孫子誠也著『エントロピーとは何だろうか』(1985・岩波書店)』▽『堀淳一著『エントロピーとは何か』(1986・講談社・ブルーバックス)』▽『小野周著『エントロピーのすべて』(1987・丸善)』▽『小島和夫著『エネルギーとエントロピーの法則――化学工学の立場から』(1997・培風館)』▽『石鍋孝夫著『熱学から熱力学へ――エントロピーを中心に』(1997・サイエンティスト社)』▽『渡辺啓著『エントロピーから化学ポテンシャルまで』(1997・裳華房)』▽『鈴木英雄・伊藤悦朗著『生体情報とエントロピー――生体情報伝達機構の論理の解明をめざして』(2000・培風館)』▽『パリティ編集委員会編、杉本大一郎著『いまさらエントロピー?』(2002・丸善)』▽『マーティン・ゴールドスタイン他著、米沢富美子・森弘之訳『冷蔵庫と宇宙――エントロピーから見た科学の地平』(2003・東京電機大学出版局)』▽『青木統夫著『非線形解析3 測度・エントロピー・フラクタル』(2004・共立出版)』▽『西野友年著『ゼロから学ぶエントロピー』(2004・講談社)』▽『朝永振一郎著『物理学とは何だろうか 下巻』(岩波新書)』
改訂新版 世界大百科事典 「エントロピー」の意味・わかりやすい解説
エントロピー
entropy
エントロピーとは,そもそも複雑さの度合を表すための熱力学的概念であり,複雑さまたはでたらめさが増すほどエントロピーは大きくなる。
複雑さの表現としてのエントロピー
理想気体が,温度一定の下で,非常にゆっくりと(すなわち準静的に)膨張してその体積がもとの体積の2倍になった状態を考えてみよう。どちらも同じ温度で平衡状態になっているが,これら二つの状態は,明らかに熱力学的に違った状態である。2倍の体積の状態のほうが熱的により乱れた状態であるといえる。なぜなら,体積が2倍となった容器の中央に仮想的な仕切りをつけたとすると,中の粒子は,もとの半分の体積の場合と比較して,仮想的な仕切りを乗り越えて両方に入り乱れることができるからである。もっと直観的にいってしまえば,ある体積の容器の中にハエを入れたときと,その2倍の体積の容器に入れたときとで,どちらのほうがハエの飛び方が複雑になるかを考えれば類推できるであろう。この乱れぐあいを定量的に表現する物理量がエントロピーなのである。理想気体が一定の絶対温度Tの下で準静的に,いいかえれば可逆的に膨張し,その際熱源から熱量Qを吸収したとすると,QとTとの比Q/Tは,初めの状態と終りの状態を固定すれば,途中のどのような経路を通って変化が進んでも一定である。もっと定量的には次のようにして説明できる。体積V1の理想気体nモル(mol)を温度一定の下で,準静的に体積V2(V2>V1)まで可逆変化させ膨張させたとき,熱源から吸収する熱量Qは外部へ対してなした仕事と等しいはずであるから,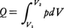 と表せる。n(mol)の理想気体に対してはその圧p,体積V,絶対温度Tの間に,pV=nRTの状態方程式が成立するから(Rは気体定数),この関係を用いて上記の式を書き換えると,
と表せる。n(mol)の理想気体に対してはその圧p,体積V,絶対温度Tの間に,pV=nRTの状態方程式が成立するから(Rは気体定数),この関係を用いて上記の式を書き換えると,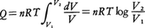 となる。すなわち,Q/T=nR log(V2/V1)となり,これは初めと終りの状態(今の場合は体積であるが)にのみ依存する状態量となる(ただし,適当に基準を決めることは必要である)。しかも,体積が増加して状態が乱れるほど,その対数に比例してQ/Tは大きくなる。このように,Q/Tが状態の乱れの度合を表していることは明らかで,このQ/TをエントロピーSと定義する。
となる。すなわち,Q/T=nR log(V2/V1)となり,これは初めと終りの状態(今の場合は体積であるが)にのみ依存する状態量となる(ただし,適当に基準を決めることは必要である)。しかも,体積が増加して状態が乱れるほど,その対数に比例してQ/Tは大きくなる。このように,Q/Tが状態の乱れの度合を表していることは明らかで,このQ/TをエントロピーSと定義する。
エントロピーという概念は,熱力学的な状態の変化を特徴づけるものとしてR.J.E.クラウジウスが導入したものであり,その名はギリシア語のentropē(反転する働きの意)に由来し,変化容量の意味で命名されたものである。
エントロピーのミクロな意味
エントロピーにミクロな意味づけを与えたのはL.ボルツマンである。彼はミクロな状態の数をWとするとき,そのエントロピーSは,S=k logWで与えられると提案した。ここで,kはボルツマン定数である。ミクロに定義されたエントロピーが,熱力学的に定義されたエントロピーと一致することを示すことは,統計力学のもっとも基本的事項である。直観的には理想気体に対するエントロピーの表式S=Q/T=nR log(V2/V1)で,とくにV2=2V1となる場合を考えるとわかりやすい。1 mol中の気体分子の数,すなわちアボガドロ数N0を用いると,R=N0kであるから,上式は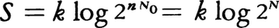 と書き直すことができる(N=nN0)。N個の粒子が仮想的な仕切りのどちら側に入るかというミクロな状態数WがW=2nで表されることを考えれば,ミクロに定義されたエントロピーと熱力学的に定義されたエントロピーの同一性が理解されよう。さらに,二つの系の熱力学的に定義されたエントロピーの和がSA+SBとなるとき,両者を併せた系のミクロな状態の数はWA・WBとなり,ミクロに定義されたエントロピーはk(log WA+log WB)で表せること(logWの加法性),またWの増大と不可逆性の関係などからも両者が一致することが理解される。
と書き直すことができる(N=nN0)。N個の粒子が仮想的な仕切りのどちら側に入るかというミクロな状態数WがW=2nで表されることを考えれば,ミクロに定義されたエントロピーと熱力学的に定義されたエントロピーの同一性が理解されよう。さらに,二つの系の熱力学的に定義されたエントロピーの和がSA+SBとなるとき,両者を併せた系のミクロな状態の数はWA・WBとなり,ミクロに定義されたエントロピーはk(log WA+log WB)で表せること(logWの加法性),またWの増大と不可逆性の関係などからも両者が一致することが理解される。
増加するエントロピー
通常,非常に小さい無限小の可逆過程に対して,微少量の熱の吸収を⊿Qとすると,系の絶対温度をTとして,この無限小可逆過程に対するエントロピーの変化dSは,dS=⊿Q/Tと表される。Sという状態量の微少な変化量であるから,数学的には⊿Q/Tが完全微分になっていることを意味している。温度Tは,示強性,すなわち体系の大きさによらない物理量であり,一方,熱量Qはエネルギーの一種で,体系の大きさに比例して加法的に多くなる示量性の物理量であるから,エントロピーは示量性の物理量である。一般の無限小過程に対しては,⊿Q≦TdSという不等式が経験的に導かれている。これが熱力学の第2法則である。もし,これが破れていると,一つの熱源から熱をとってそれを全部仕事に変える第2種永久機関が作れることになる。等号は可逆過程に対して成立し,不等号が成り立つ過程を不可逆過程という。すなわち,同じエントロピーの変化dSに対して,熱量の変化がTdSより小さい過程は不可逆であり,逆にいえば,同じ熱量⊿Qの変化に対して,エントロピーが⊿Q/Tより大きな変化をする過程が不可逆過程であるということができる。とくに外部から完全に孤立した系では,熱の出入りは0,すなわち⊿Q=0であるから,熱力学の第2法則はdS≧0と表される。すなわち一つの孤立系においては,その系のエントロピーの総和は,その系内に可逆過程が生じても不変に保たれ,不可逆過程が生じた場合には増加し,どんな場合でも減少することはないということを示しているのである。これが孤立系に対するエントロピー増大の原理である。自然界に起こる過程は,摩擦,熱伝導など不可逆過程が多く,したがって自然界(宇宙)を孤立系とみなせばエントロピーの総和はその極大値に向かって増加していることになる。
→可逆変化 →不可逆変化
エントロピーと熱機関の効率
エントロピーの概念を用いると,理想的な熱機関の効率ηを計算することができる。最大効率をもつ理想的な熱機関の効率ηは,エネルギー保存則と熱力学の第2法則より,エントロピーの変化をなるべく少なくして,外にとり出す仕事を最大にする過程,すなわち可逆過程に対する効率として求められる。絶対温度T1の高温熱源から熱量⊿Q1=T1dSをとり出し,その一部を仕事⊿Wに変換し,高温熱源からとり出したエントロピーdSをそっくり絶対温度T2の低温熱源に可逆的に返すことによって理想的な熱機関が設定される。すなわち,低温熱源に熱量⊿Q2=T2dSだけ渡すことになるから,効率ηは,η=⊿W/⊿Q1=(⊿Q1-⊿Q2)/⊿Q1=(T1-T2)/T1によって与えられる。したがって,低温熱源の温度T2が小さいほど効率ηは大きくなり,T2=0でη=1となる。それは,温度が低いほど熱量の変化は少なく,エントロピーの受容がますます大きくなるからである。これを裏返しにいうと,低温になるほど,その状態を作り出すのにますます多くのエントロピーを外にとり出さなければならなくなり,絶対0度に到達するのは実現不可能なことを意味している。
なお,このエントロピーの概念は,情報量を表すのにも使われているが,これについては〈情報理論〉の項目を参照されたい。
執筆者:鈴木 増雄
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「エントロピー」の意味・わかりやすい解説
エントロピー(熱)【エントロピー】
→関連項目永久機関|ゴム状弾性|時間(物理)|自由エネルギー|熱力学|不可逆変化|ボルツマン
エントロピー(情報)【エントロピー】
→関連項目熱力学の法則
出典 株式会社平凡社百科事典マイペディアについて 情報
化学辞典 第2版 「エントロピー」の解説
エントロピー
エントロピー
entropy
系が絶対温度Tのもとに外界からの準静的過程によって熱量Qを得たとき,関数
S = Q/T
を導入してこれをエントロピーという.微小熱量dQ′に対して,エントロピーの微小変化dSは全微分となり,Sは状態量の一つになる(dQ′のダッシュは全微分でないことを示す).エントロピーという用語はR.J.E. Clausius(クラウジウス)がはじめて用いたことばで,ギリシア語の“変化”という意味からきている.熱力学第二法則は孤立系ではエントロピーが決して減少しないこと,非可逆変化によってつねに増大することを示す.統計力学によると,系のエントロピーは系全体のエネルギーE,粒子数N,体積Vが指定されたとき,その系に可能な状態の数の全体をWとして,
S = k ln W
という関係で与えられる(kはボルツマン定数).この関係式は近似的に,1粒子のエネルギー固有値を ε1,ε2,…,その各固有値にある粒子数を n1,n2,…としたとき,ある特定の一組 n10,n20,…に対して系の状態の数W{nj}は極大となり,その値 W0{nj0}を用いて
S = k ln W0
と表される.この近似は極大値を与える組{nj0}が圧倒的確率でもって実現可能であることを示す.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
ブリタニカ国際大百科事典 小項目事典 「エントロピー」の意味・わかりやすい解説
エントロピー
entropy
エントロピー[情報量]
エントロピー[じょうほうりょう]
entropy
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
図書館情報学用語辞典 第5版 「エントロピー」の解説
エントロピー
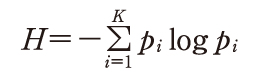 と定義した.熱力学のエントロピーと同じ形をしているので情報源のエントロピーといい,熱力学では乱雑さを表現しているのに対し,情報では不確実さを表している.情報理論では,原則として対数の底に2をとるので,その単位はビットになる.
と定義した.熱力学のエントロピーと同じ形をしているので情報源のエントロピーといい,熱力学では乱雑さを表現しているのに対し,情報では不確実さを表している.情報理論では,原則として対数の底に2をとるので,その単位はビットになる.出典 図書館情報学用語辞典 第4版図書館情報学用語辞典 第5版について 情報
最新 地学事典 「エントロピー」の解説
エントロピー
entropy
エネルギーのでたらめな広がりの目安を与える状態量。熱力学の第二法則は,エントロピーの概念を用いて次のように表現できる。孤立系のエントロピーは,不可逆変化の過程で常に増加する。熱力学的状態量としてのエントロピーSは温度Tにおいて,可逆的に,物質あるいは系に与えられた熱量Qrを用いて,次のように定義される。dS=dQr/T, したがって,0Kの単体のエントロピーは0で,そのほかはすべて正の値をもつ。語源はギリシア語のtrope(変化)に由来する。
執筆者:吉田 尚弘
出典 平凡社「最新 地学事典」最新 地学事典について 情報
栄養・生化学辞典 「エントロピー」の解説
エントロピー
世界大百科事典(旧版)内のエントロピーの言及
【温度】より
…理想的な熱機関とは可逆的に働く熱機関で,カルノーサイクルに代表される。上で絶対温度の比を定義した関係はQ1/T1=Q2/T2と書きなおされ,可逆過程でエントロピーS=Q/Tが保存されることを表している。絶対温度はエントロピーという重要な量の導入を可能にしたのである。…
【可逆変化】より
…一般に,摩擦による熱の発生など仕事が熱に変わる過程は典型的な不可逆過程であり,一方,熱の発生を伴わない電磁気現象は可逆過程である。 絶対温度Tの物質系の可逆変化で,熱の吸収を⊿Qとすれば,この系のエントロピーの増大⊿Sは⊿S=⊿Q/Tで与えられる。不可逆変化では⊿S>⊿Q/Tの不等式を満たす。…
【情報】より
…これだと,確率が小さいほど情報量が大きいという心理的事実と合うのである。この定義によれば-符号あたりの平均情報量Hは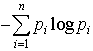 となり,熱力学でいうエントロピーと同じ形をしているので〈エントロピー〉と呼ばれる。ただし熱力学の場合と異なり負号がついているので〈負エントロピー(ネゲントロピーnegentropy)〉ということもある。…
となり,熱力学でいうエントロピーと同じ形をしているので〈エントロピー〉と呼ばれる。ただし熱力学の場合と異なり負号がついているので〈負エントロピー(ネゲントロピーnegentropy)〉ということもある。…
【情報量】より
…そこで,log2Mを,M個の文字からなるアルファベットをもつ情報源のハートリーHartley情報量と呼んでいる。
[エントロピー]
もし,1からMまでの文字が出現する確率p1,p2,……,pMが知られており(すなわち,どの文字がどの程度によく出やすいかなどの情報をもっている場合),各文字を(先ほどのように8ビットと制限せず)長さの異なるビット列に対応させても構わないとすれば,各文字に対応したビット列(符号語)の長さの平均値を,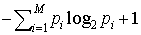 以下にできることが示される。これは,もちろん,多くの文字を対応した符号語の連なりとして仕立てた長いビット列が与えられたとき,符号語と符号語の切れ目を識別できるような(分節可能な)対応関係が保証されているという条件のもとでの話である。…
以下にできることが示される。これは,もちろん,多くの文字を対応した符号語の連なりとして仕立てた長いビット列が与えられたとき,符号語と符号語の切れ目を識別できるような(分節可能な)対応関係が保証されているという条件のもとでの話である。…
【数理統計学】より
…しかし,彼の理論では分布の関数形はわかっていて,パラメーターのみが未知とする立場をとっている。ところが尤度関数の意味を問いなおせば,情報量,あるいはエントロピーの概念が重要な役割を果たしていることに思いあたる。これから1973年に赤池弘次(1927‐ )によって提唱された情報量基準AICの概念を理解する手がかりが得られよう。…
【データ圧縮】より
…このときどこまで圧縮が可能かという問題に対し,C.E.シャノンによる情報理論はデータを発生する情報源を確率モデルとして定式化し,圧縮後の1文字当りの平均ビット長の下限を与える形で限界を示した。その下限値は無歪み圧縮の場合はエントロピーと呼ばれる。歪みありの圧縮の場合はレート・歪み理論と呼ばれる理論体系が構築されている。…
【熱】より
… 力学的エネルギーに加えて電磁気的エネルギー,化学的エネルギーそして熱エネルギーと,すべての種類の現象にかかわるエネルギー(19世紀後半になるまでは“力”と呼ばれていた)が,相互に変換され,しかもあらゆる過程で保存される量であるというエネルギー保存則は,19世紀後半になってR.マイヤー,ジュール,H.ヘルムホルツら多くの人々の貢献により広く認識されるようになった。しかし熱がエネルギーであるというだけでは不十分であって,温度およびエントロピーとの関係も含めて古典物理学の枠内で熱の概念が確立されたのは,R.クラウジウス,ヘルムホルツ,ケルビン(W.トムソン)らによって熱力学の体系が作られるのをまたなければならなかった。さらに,20世紀にかけてJ.C.マクスウェル,L.ボルツマン,J.W.ギブズらによって気体運動論,そして統計力学が形成され,物質を構成する原子・分子の力学から熱現象を理解することが可能となった。…
【符号化】より
…ふつう符号化により得られる形態は記号列であるが,それらの全体を〈符号〉といい,本来の形態に戻し,情報を復元・再現することを〈復号〉という。データ圧縮,誤り訂正符号化,暗号化は,そろって,情報を量として扱う学問体系〈情報理論〉の主要なテーマであるが,データ圧縮が情報源に適合する符号化として,真正の情報量(エントロピー)の近くまでデータ長を削減するのに対し,誤り訂正符号化は通信路に適合する符号化として,情報量としては余分なデータ長を追加する。ここでは,後者の誤り訂正符号化について述べる。…
※「エントロピー」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...