ペアノ曲線(ペアノキョクセン)とは？意味や使い方

デジタル大辞泉「ペアノ曲線」の意味・読み・例文・類語

ペアノ‐きょくせん【ペアノ曲線】

空間充塡曲線として最初に発見された曲線。1890年にペアノが発見。正方形を単位として再帰的に定義され、その極限をとることで領域が曲線で埋め尽くされる。

出典　小学館デジタル大辞泉について　情報 | 凡例

日本大百科全書(ニッポニカ) 「ペアノ曲線」の意味・わかりやすい解説

ペアノ曲線
ぺあのきょくせん

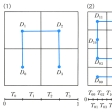
平面や空間の一部分をうずめ尽くす曲線をいう。曲線とは、一般にその点の座標が一つの実変数tの連続関数となっているようなものをいう。そこで、曲線というと、滑らかな線の形になっているものだけを想像するが、そうでない曲線もある。イタリアの数学者ペアノは1890年に、正方形の内部をうずめ尽くすような曲線の例をつくった。図の(1)のように、正方形D、および区間［0,1］を4等分して、正方形D_iD_iと線分T_iT_iを対応させる。このような操作を図の(2)、図の(3)のように順次行っていく。正方形の列
　D_i⊃D_ij⊃D_ijk⊃……
に対して、ただ一つの共有点x_ijk…が定まるが、この点を、線分の列
　T_i⊃T_ij⊃T_ijk⊃……
の共有点t_ijk…に対応させる。対応t_ijk…→x_ijk…は、区間［0,1］から正方形D上への連続な写像で、したがって正方形Dをうずめ尽くすような曲線となる。なお、A⊂Bは、AがBの部分集合であることを表す。以上のように構成された曲線には、二重点、四重点が無限に現れる。一般に正方形をうずめ尽くすようなペアノ曲線には三重点以上の重複点が無限に多く現れることが知られている。ブラウアーの領域の不変性の定理によれば、線分と正方形を連続的に1対1に対応させることはできない。ペアノ曲線は、1対1という条件を落とせば、線分から正方形の上への対応が可能であることを示している。一方、曲線の定義に、重複点が現れないという条件を加えたものを、ジョルダン曲線という。ジョルダン曲線は、正方形をうずめ尽くすようなことはできない。常識的に考えたときの曲線の性質をもっている。

［竹之内脩］

[参照項目] | 曲線 | ジョルダンの曲線定理

出典　小学館　日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について　情報 | 凡例

改訂新版　世界大百科事典「ペアノ曲線」の意味・わかりやすい解説

ペアノ曲線 (ペアノきょくせん)
Peano curve

曲線とは連続的に動く点の描く図形と考えられる。したがって，例えば平面上に直交座標系を設定すれば，その平面上の曲線とは，fおよびgを区間［a，b］上で定義された連続関数としたとき，a≦t≦bであるようなすべてのtに対する点（f（t），g（t））のつくる図形ということができる。しかしこのように曲線を定義するとき，意外なものが曲線の仲間に入ってくることをG.ペアノは1890年に発見した。すなわち，彼は正方形のすべての点をくまなく通るような曲線の実例を与えて当時の数学界を驚かせた。このように面積をもつ図形を塗りつぶすような曲線の例はその後も多く与えられた。このような曲線を総称してペアノ曲線という。ヒルベルトによる例を次にあげておく。一つの線分と一つの正方形をとり，それらを次々と4等分していく。そしてそれによって生ずる各部分へ，図のように隣接した部分線分には隣接した部分正方形が対応するように順次に番号をつけていく。ところで線分上の点は縮小していく部分線分の列i₁⊃i₁i₂⊃i₁i₂i₃⊃……の極限の点として表され，同様に正方形の点は縮小していく部分正方形の列j₁⊃j₁j₂⊃j₁j₂j₃⊃……の極限の点として表される。それでi₁⊃i₁i₂⊃i₁i₂i₃⊃……で表される線分の点tには同じ列で表される正方形の点（x，y）を対応させる。このときx＝f（t），y＝g（t）はtに関して連続となって曲線が得られるが，これは正方形を埋めるペアノ曲線となる。なお，平面上のペアノ曲線では，その曲線が少なくとも三度通る点が無限に多く存在することが知られている。
執筆者：中岡稔

出典　株式会社平凡社「改訂新版　世界大百科事典」改訂新版　世界大百科事典について　情報

ブリタニカ国際大百科事典小項目事典「ペアノ曲線」の意味・わかりやすい解説

ペアノ曲線
ペアノきょくせん
Peano curve

G.ペアノは，連続曲線であって，一つの正方形の内部を埋めつくすものの例を与えた。このような平面を埋めつくす曲線をペアノ曲線という。ペアノ曲線には多数の重複点がある。

出典　ブリタニカ国際大百科事典小項目事典ブリタニカ国際大百科事典小項目事典について　情報

ASCII.jpデジタル用語辞典「ペアノ曲線」の解説