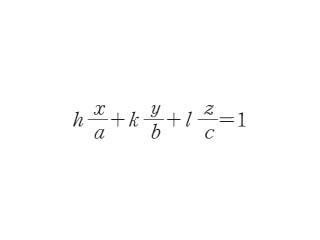ミラー指数
みらーしすう
Miller indices
イギリスの鉱物学者W・H・ミラーが結晶面の記号として1839年に採用したもの。天然の鉱物結晶や実験室で溶液から成長させた結晶は、普通、平面によって囲まれた規則正しい多面体の外形をもつ。この外形に現れている平面を結晶面という。ミラー指数は面指数ともいい、各結晶面の種類を指定するための三つの整数(普通これらにh、k、lの文字をあてる)からなる指数である。各結晶面を括弧付きの記号(hkl)で表す。いま結晶を構成する最小単位である単位胞(たんいほう)(単位格子)は三つのベクトルa、b、cがつくる平行六面体であるが、このa、b、cに平行に3本の結晶軸を定める。この結晶軸の方向に座標軸x、y、zをとるとき(座標軸はかならずしも直交していない)、結晶面(hkl)は、各軸を原点からそれぞれ
X=a/h, Y=b/k, Z=c/l
の距離のところで切るような平面である。ただしa、b、cは定数で、比a:b:cが着目する結晶の種類に固有な値の比率(これをその結晶の軸率という)に相当する。結晶面の方位は比X:Y:Zによって、したがって比h:k:lによって決まる。結晶軸の負の部分で交わる面の指数は負となるが、-hは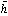 と書く。たとえば(h-kl)は(h
と書く。たとえば(h-kl)は(h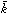 l)で表す。また、ある結晶軸に平行な面は、その軸と無限遠で交わるとして、その指数は0とする。(110)とはx、y軸とa、bで交わりz軸とは平行な面である。h、k、lは公約数を含みうる。h、k、lを最大公約数で割った整数をh*、k*、l*とするとき、(hkl)と(h*k*l*)はお互いに平行な結晶面であるが、混乱を避けるため互いに素の整数h*、k*、l*をミラー指数(面指数)に選ぶことが多い。各結晶面はその結晶がもつ結晶格子(空間格子)の格子面に平行であり、格子面もまたミラー指数によって指定することができる。
l)で表す。また、ある結晶軸に平行な面は、その軸と無限遠で交わるとして、その指数は0とする。(110)とはx、y軸とa、bで交わりz軸とは平行な面である。h、k、lは公約数を含みうる。h、k、lを最大公約数で割った整数をh*、k*、l*とするとき、(hkl)と(h*k*l*)はお互いに平行な結晶面であるが、混乱を避けるため互いに素の整数h*、k*、l*をミラー指数(面指数)に選ぶことが多い。各結晶面はその結晶がもつ結晶格子(空間格子)の格子面に平行であり、格子面もまたミラー指数によって指定することができる。
[三宅静雄・石田興太郎]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
ミラーしすう
ミラー指数
Miller’s indices
面指数とも。結晶の軸率をa:b:cとしたとき,3軸をそれぞれ軸率の比で切る面を(111)として表現する。他の面の面指数はそれぞれ単位長を切る逆比で示し,例えば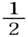 a:
a: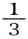 b:1cで切る面は(231)のように表現され,一般に(hkl)で表される。また,ある軸に平行な面は無限大の逆数0を用いて(102)のようになる。六方および三方晶系では側軸が3本あるので(hkil)のように4指数で示す。この際のh+k+i=0。結晶面を表現するには,( )でくくったこの指数が用いられるが,X線回折指数の場合にはhklのように( )なしで示す。
b:1cで切る面は(231)のように表現され,一般に(hkl)で表される。また,ある軸に平行な面は無限大の逆数0を用いて(102)のようになる。六方および三方晶系では側軸が3本あるので(hkil)のように4指数で示す。この際のh+k+i=0。結晶面を表現するには,( )でくくったこの指数が用いられるが,X線回折指数の場合にはhklのように( )なしで示す。
執筆者:高野 幸雄
参照項目:有理指数の法則
参照項目:結晶面の表記,対称操作とその投影
出典 平凡社「最新 地学事典」最新 地学事典について 情報
Sponserd by 
ミラー指数
ミラーシスウ
Miller indices
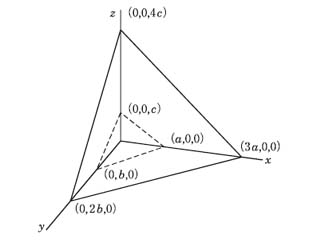
面指数ともいう.結晶面または格子面を,その面が各結晶軸となす傾きを用いて定義する指数.単位格子の各稜oa,ob,ocを,おのおのh,k,l等分した切片を通る面およびそれに平行な面のグループを(h k l)で表す.図の斜線の面のミラー指数は(211)である.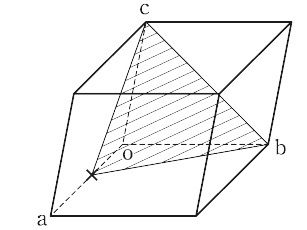 h,k,lは面の傾きを与えるだけであるから,互いに素な0を含む整数である.-hを
h,k,lは面の傾きを与えるだけであるから,互いに素な0を含む整数である.-hを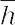 のように書く.三方晶系と六方晶系では(h k l)を(h k i l)と書くこともある(ただし,i = -h - k).結晶面h k lおよびこれと結晶学的に同価な面の全体は{h k l}で表す.
のように書く.三方晶系と六方晶系では(h k l)を(h k i l)と書くこともある(ただし,i = -h - k).結晶面h k lおよびこれと結晶学的に同価な面の全体は{h k l}で表す.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
Sponserd by 
ミラー指数
ミラーしすう
Miller indices
結晶面または空間格子の格子面を表示するのに用いられる指数。結晶面が結晶軸 a,b,c を a/h,b/k,c/l で切る平面に平行であるとき,h,k,l は常に有理数となるが,これらに一定数を乗じて互いに素な整数としたものをミラー指数といい,(hkl) で表わす。ある結晶軸に平行な面のミラー指数を0とし,また -h は 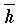 と表わす。 h ,k ,l の符号が異なる格子面が対称性によって同等である場合,それらを総括して {hkl} で表わす。
と表わす。 h ,k ,l の符号が異なる格子面が対称性によって同等である場合,それらを総括して {hkl} で表わす。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
法則の辞典
「ミラー指数」の解説
ミラー指数【Miller index】
結晶面は,結晶軸 x,y,z を座標軸とする平面方程式として表現できる.すなわち
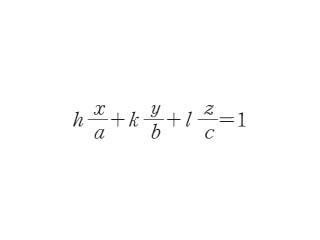
である.ここで x,y,z は座標,a,b,c は軸率である.だから h,k,l の組(整数比となるようにする)として結晶の面を表現できることになる.これを括弧(丸括弧)の中に入れて(h,k,l)のように記すが,これをミラー指数という.これによって結晶面を記載するのがミラーの記号法*である.
出典 朝倉書店法則の辞典について 情報
Sponserd by 
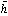 と書く。たとえば(h-kl)は(h
と書く。たとえば(h-kl)は(h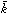 l)で表す。また、ある結晶軸に平行な面は、その軸と無限遠で交わるとして、その指数は0とする。(110)とはx、y軸とa、bで交わりz軸とは平行な面である。h、k、lは公約数を含みうる。h、k、lを最大公約数で割った整数をh*、k*、l*とするとき、(hkl)と(h*k*l*)はお互いに平行な結晶面であるが、混乱を避けるため互いに素の整数h*、k*、l*をミラー指数(面指数)に選ぶことが多い。各結晶面はその結晶がもつ結晶格子(空間格子)の格子面に平行であり、格子面もまたミラー指数によって指定することができる。
l)で表す。また、ある結晶軸に平行な面は、その軸と無限遠で交わるとして、その指数は0とする。(110)とはx、y軸とa、bで交わりz軸とは平行な面である。h、k、lは公約数を含みうる。h、k、lを最大公約数で割った整数をh*、k*、l*とするとき、(hkl)と(h*k*l*)はお互いに平行な結晶面であるが、混乱を避けるため互いに素の整数h*、k*、l*をミラー指数(面指数)に選ぶことが多い。各結晶面はその結晶がもつ結晶格子(空間格子)の格子面に平行であり、格子面もまたミラー指数によって指定することができる。

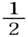 a:
a: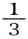 b:1cで切る面は(231)のように表現され,一般に(hkl)で表される。また,ある軸に平行な面は無限大の
b:1cで切る面は(231)のように表現され,一般に(hkl)で表される。また,ある軸に平行な面は無限大の h,k,lは面の傾きを与えるだけであるから,互いに素な0を含む整数である.-hを
h,k,lは面の傾きを与えるだけであるから,互いに素な0を含む整数である.-hを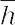 のように書く.
のように書く.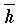 と表わす。 h ,k ,l の符号が異なる格子面が対称性によって同等である場合,それらを総括して {hkl} で表わす。
と表わす。 h ,k ,l の符号が異なる格子面が対称性によって同等である場合,それらを総括して {hkl} で表わす。