多変量解析（読み）タヘンリョウカイセキ（英語表記）multivariate analysis

デジタル大辞泉

たへんりょう‐かいせき〔タヘンリヤウ‐〕【多変量解析】

対象を特徴づける複数の変数を同時に解析することで、対象を分類したり、変数同士の相関関係を調べたりする統計的手法。

出典　小学館

最新 心理学事典

たへんりょうかいせき
多変量解析
multivariate analysis

多変量解析とは，実験や調査において関心の対象となっている個体から複数の観測値が得られるとき，その複数の変数間の相関の構造や因果関係について分析する手法を指す。すなわち，個体から複数変数ｙ¹，…，ｙ^pが観測されるとき，各変数を別々に分析するのではなく，複数変数をまとめたベクトルｙ＝［ｙ¹，…，ｙ^p］′を一つの観測単位として扱う統計解析の諸方法を総称する。多変量解析は，19世紀末から20世紀初頭のゴールトンGalton,F.やピアソンPearson,C.の回帰・相関の研究に萌芽し，同時期にスピアマンSpearman,C.E.が因子分析を着想している。そして，フィッシャーFisher,R.A.，ホテリングHotelling,H.，ラオRao,C.R.やアンダーソンAnderson,T.W.などによって一変量の統計理論が多変量に拡張され，基本的方法が体系化される。その後の特筆すべき動きに，1960年代後半からのヨレスコフJöreskog,K.G.らによる構造方程式モデルの研究や，柳井晴夫が進めた多変量解析の基礎としての射影行列の研究がある。

　多変量解析の諸方法はさまざまな観点で大別されるが，その一つは，次元縮約，因果分析，個体の分類といった目的ごとの分類であろう。以下，すべての変数の平均は0と想定して，基本的な諸方法を記す。

【次元縮約】　個体を表わす添え字ｉをｙにつけて，個体ｉのデータをｙⁱ＝［ｙⁱ¹，…，ｙ^ip］′と表わそう。各変数の重みつき合成得点



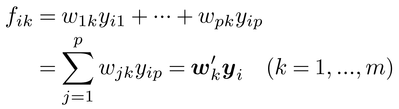
が，もとのｐ変数の個体間変動をできるだけよく縮約するような重みベクトルｗ^k＝［ｗ^1k，…，ｗ^pk］′（ｋ＝1，…，ｍ）を求める方法が主成分分析principal component analysis（PCA）である。たとえば，ｐ＝5の5次元データに対して重みの種類ｍを2とすれば，目には見えない5次元空間内での個体の散布が，ｗ¹，ｗ²（ｋ＝1，2）に基づく得点［ｆⁱ¹，ｆⁱ²］′の2次元散布図で近似的に可視化される。個体ｉから，ｙⁱとともに別種の変数群ｘⁱ＝［ｘⁱ¹，…，ｘ^iq］′が観測されるとき，それぞれの変数群の重みつき合成得点



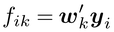
と



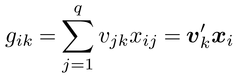
の相関係数のｋに関する総和を最大にするｗ^kとｖ^kを求める方法が正準相関分析canonical correlation analysisであり，変数群間の相関関係を少数（ｍ）次元の得点に縮約させる方法と位置づけられる。

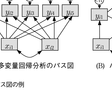
【観測変数間の因果分析】　変数間の因果関係や予測の関係を示すためには，パス図path diagramが便利である（図）。パス図においては，変数を四角で示し，観測されていない潜在変数を円あるいは楕円で囲み，また変数間の因果関係を一方向の矢印，相関関係を双方向の矢印で示す。パス図（Ａ）に例示するように，ｙⁱ＝［ｙⁱ¹，…，ｙ^ip］′の各要素が結果，ｘⁱ＝［ｘⁱ¹，…，ｘ^iq］′が原因である因果関係は，誤差ｅ^ijを用いて



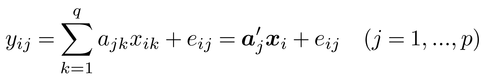
とモデル化される。ここで，係数ベクトルａ^j＝［ａ^j1，…，ａ^jq］′をp×qの行列Ａ＝［ａ¹，…，ａ^p］にまとめ，誤差ベクトルをｅⁱ＝［ｅⁱ¹，…，ｅ^ip］′と表わせば，上記のモデルはｙⁱ＝Axⁱ＋eⁱと表わせる。このモデルのもとで誤差2乗和を最小にするＡを求める分析を，多変量回帰分析multivariate regression analysisという。誤差間に相関がない場合，この解と各結果ｊについてｙ^ij＝ａ′^jｘⁱ＋ｅ^ijの誤差2乗和



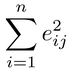
を最小にする重回帰分析multiple regression analysisの解は一致する。

　パス図（Ｂ）に例示するように，ｙⁱ＝［ｙⁱ¹，…，ｙ^ip］′の要素間にも因果関係を反映させ，因果関係を示すパスのみを残す分析をパス解析path analysisとよび，そのモデルはｙⁱ＝Ａ［ｙⁱ，ｘⁱ］＋ｅⁱのように書ける。パス解析では，変数間の因果関係を表わすモデル，言い換えれば，パス図における矢印の結び方を分析者自身が考え，データへの適合度が高いモデルを選定することになる。

【潜在変数を伴う因子分析】　多変量回帰分析のモデルｙⁱ＝Axⁱ＋eⁱのｘⁱが，観測されない潜在変数latent variablesのｆⁱに代わったｙⁱ＝Afⁱ＋eⁱが，探索的因子分析exploratory factor analysisのモデルである。これに対して，パス図（Ｃ）に例示するように，パスが特定の変数どうしに限られる，つまりＡの要素のいくつかは0であるという仮定のもとに行なう因子分析を確認的因子分析confirmatory factor analysisという。これを発展させて，潜在変数どうしにも因果を考え，［ｙⁱ，ｆⁱ］＝Afⁱ＋eⁱのように書けるモデルを構造方程式モデルstructural equation model（SEM）という。因子分析・パス解析・SEMの多くのモデルは，それらの解法が共分散に基づく点で共通するため，共分散構造分析covariance structure analysisと総称されることがある。ただしSEMは平均に対するモデルを含み，共分散構造に関するモデルに限定されない。なお，1990年代より発展した独立成分分析independent component analysisは，因子を互いに独立した信号の発信源とみなして，その同定をめざす多変量解析法と位置づけられる。

【個体の分類】　たとえば，来診者を健常群・風邪の群・花粉症の3群のいずれかへ分類するといった，個体の所属群の判別を統計的に行なう方法を，判別分析discriminant analysisと総称する。最も基本的な2群の線形判別分析では，



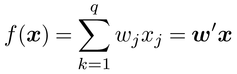
と閾値ｃの大小比較で群判別を行なうことを想定して，所属群が既知の複数個体のデータからｗ＝［ｗ¹，…，ｗ^q］′とｃの最適値を推定した後，所属群が未知の個体のｘをｆ（ｘ）に代入して，その個体が2群のいずれに属するかを判別する。なお判別すべき群があらかじめ与えられていない場合に，群を構成する手法，すなわち似た個体同士は同一群，隔たる個体同士は異なる群に属するように個体を群分けする手法を，クラスター分析cluster analysisと総称する。

【主成分分析に関連する手法】　主成分分析は，重みつき合成得点をベクトルにしたｆⁱ＝［ｆⁱ¹，…，ｆ^im］′を用いてｙⁱ＝Bfⁱ＋eⁱとモデル化することもでき，これは探索的因子分析のモデルｙⁱ＝Afⁱ＋eⁱと見かけ上は同じであるが，誤差ｅⁱに対する仮定の違いから両分析は異なる。たとえば，三変数「学部・性別・希望職種」の観測値が「工学部・男性・技術職」といったカテゴリーであるデータを分析するために拡張された主成分分析は，多重対応分析multiple correspondence analysisまたは数量化法3類などとよばれ，カテゴリーを数量化したベクトルを解として与える。カテゴリー同士の距離的なデータから，カテゴリーの座標値を求める方法は，多次元尺度法multidimensional scalingとよばれる。

【多変量推測統計】　確率変数ベクトル［Ｙ¹，…，Ｙ^p］′が実現値［ｙ¹，…，ｙ^p］′を取る確率密度を表わす理論分布の中でも代表的なものは，正規分布を一般化した多変量正規分布multivariate normal distributionである。こうした理論分布に基づき，ここまで記した諸方法の解に関する仮説検定法や区間推定法が考案されている。なお，多変量回帰分析のモデルｙⁱ＝Axⁱ＋eⁱのｘⁱが，個体の所属群を1か0の要素で表わすベクトルであるとき，Ａの列は各群の平均ベクトルとなり，このモデルを基礎として平均ベクトルの群間等値の仮説などを検定する手法を多変量分散分析multivariate analysis of varianceとよぶ。　→因子分析　→回帰分析　→カテゴリカル・データ分析　→クラスター分析　→構造方程式モデル　→主成分分析　→多次元尺度法
〔足立 浩平〕

図 パス図の例

出典　最新 心理学事典

日本大百科全書(ニッポニカ)

多変量解析
たへんりょうかいせき

n個の個体があり、そのおのおのについてp種の変量x₁、……、x_pが観測されているとする。x₁、……、x_pのうちの二つの変量の間の相関関係は全部で、_pC₂個あるが、これらをもとにして、x₁、……、x_pの間の全体的関係を統計的に解析するのが多変量解析である。多変量というのは、問題にする変量がいくつもあるからである。

　コンピュータの発達と普及に伴い、とくに社会科学の分野において多変量解析の手法が広く用いられるようになった。多変量解析には、主成分分析、因子分析、判別分析、正準相関分析などいくつもの手法があるが、これらの手法についてのプログラムが統計解析パッケージの一部として多くのコンピュータに準備されている。しかし複雑多様な現実問題に対して完全な解答を与えるところまで理論が進歩しているわけではない。形式的な計算結果だけを過信することは危険であって、問題の定式化の妥当性についての十分な吟味が必要である。次に、主成分分析および因子分析について簡単に説明する。

［古屋　茂］

主成分分析

この方法はp個の互いに相関をもつ変量x₁、……、x_pのもつ情報を、pより小さいm個の互いに相関のない変量z₁、……、z_mに要約しようとするものである。

　z₁、……、z_mは次のようにして定める。変量x_iをすべて平均値が0、分散が1であるように標準化しておく。x_iとx_jの相関係数を(i,j)成分とするp×p行列をx₁、……、x_pの相関行列という。この相関行列の固有値を大きいほうから順にm個とって、λ₁、……、λ_mとし、固有値λ_iに対応する固有ベクトルの第j成分をl_ijとする。このl_ijを用いて
　　z₁=l₁₁x₁+……+l_1px_p
　　z₂=l₂₁x₁+……+l_2px_p
　　　　…………………
　　z_m=l_m1x₁+……+l_mpx_p
によってz₁、……、z_mを定めるのである。このz_iを第i主成分という。こうして得られたz₁、……、z_mは互いに無相関になっている。

［古屋　茂］

因子分析

この方法の目的は、多くの変数の間にある相関関係を分析して、それらの変数の背後にある潜在的共通性を探ることにある。潜在的共通性といっても一般的な形では取扱いが困難なので、与えられた変量の一次結合で表されるものを考える。観測される変量がp個あるとして、それらをx₁、……、x_pとする。これらの変量のおのおのは、比較的少数の直接には観測されない変量y₁、……、y_qによって次の形に表されているものと仮定する。

　　x₁=a₁₁y₁+……+a_1qy_q+d₁
　　x₂=a₂₁y₁+……+a_2qy_q+d₂
　　　　…………………
　　x_p=a_p1y₁+……+a_pqy_q+d_p
ただし係数a_ijは未知の母数である。また変量y₁、……、y_q、d₁、……、d_pは統計的に独立であると仮定する。y₁、……、y_qを潜在共通因子といい、d₁、……、d_pを特殊因子という。

　ここでx₁、……、x_p、y₁、……、y_qはすべて平均値が0、分散が1と標準化されているものとする。a_ijを(i,j)成分とするp×q行列をA、x₁、……、x_pの相関行列をRとすると
　　（＊）　R=A^tA+Δ
ただしΔは(i,i)成分がd²_iの平均値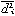であるようなp次対角行列である。なお、
　　h²_i=a²_i1+……+a²_iq
と置くと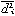=1-h²_iであって、h²_iを共通度とよぶ。われわれが知りうるのは行列Rだけである。このRが前記の式（＊）のように分解できるように、共通因子の数q、行列Aを推定し、これらの推定値を用いて共通因子y_iの値を求めようというのが因子分析の考えである。

［古屋　茂］

『ケンドール著、浦昭二・竹並輝之訳『多変量解析の基礎』（1972・サイエンス社）』▽『柳井晴夫・高根芳雄著『新版　多変量解析法』（1985・朝倉書店）』

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

多変量解析 (たへんりょうかいせき)
multivariate analysis

多変量，すなわち多数の統計的変量の，相互依存関係や従属的関係の解析を目的とする統計的手法とその理論の総称。20世紀初めから，F.ゴールトン，K.ピアソン，R.A.フィッシャー，マハラノビスP.C.Mahalanobisらによって生物学の分野に，C.E.スピアマン，サーストンL.L.Thurstone，H.ホテリングらによって計量心理学などの分野に先駆的に導入され，最近ではコンピューター利用の急速な発展により，統計処理が容易に行えるようになったことによって，工程解析，市場分析，品質解析，財務分析，社会調査，計量診断，薬効検定などへ広く活用されている。歴史的には，1変量の正規分布を前提とする平均や分散に関する推定や検定の理論を多変量正規分布の場合に拡張する研究が先行したが，現在では，n個の対象のおのおのについてp種類の変数の値が観察されている形式を基本とする多変数データを実際的に解析する種々の手法が開発されている。回帰分析，判別関数（判別分析），主成分分析，因子分析，クラスター分析などが主要な手法であり，ほかに，正準相関分析（相関分析），多次元尺度構成法，数量化理論，潜在構造分析などが含まれる。時間的変化を追う時系列データの解析手法や，機械の寿命とか生物の生存に関するデータの解析などは，多変数データであっても多変量解析に含めないのが普通である。しかし，そのような区別は便宜的なものであって，データ解析は目的に即した総合的な立場で進めるべきものであろう。

　解析したい多変数データは，計画的実験によるデータや無作為抽出を経た標本調査のデータの場合より，むしろ日常的に観察されているものが多い。例えば，製鉄所の一貫した工程で作られた鉄板の種々の製品特性は，工程条件や原料のデータとともに記録され，その記録されたデータにもとづいて解析されている。そこでは，工程条件を実験的に大幅に変化させることはできず，モデルの探索や製品特性の予測は大変困難であるが，注意深いデータの吟味と適切な回帰分析の利用によって新製品の開発にまで効果をあげている。考古学者は，たまたま発掘された人骨や土器・装身具類について，種々の特性を測定した多変数データによって分類や人種，時代等の判別を行っている。企業の財務分析家は，多数の企業の売上高，原価，利益，資本，負債，従業員数などの多くのデータを調査し，企業の財務状況を総合的に評価する指標を主成分分析を利用して作り出している。現在では，多変数データを用意すれば，標準的手法についての必要な計算を行ってくれるコンピューター用ソフトウェアが使用できるようになっており，道具として使いこなすことが必要である。
執筆者：吉沢 正

出典　株式会社平凡社「改訂新版　世界大百科事典」

岩石学辞典

多変量解析

対象を特徴づけるには，一般に複数個の数値が用いられる．たとえば人の大きさを言い表すには身長,体重，胸囲，胴回り，座高など複数個の数値が必要である．この場合，どれか一つの特性値に注目して解析する統計的方法に対し，ベクトル値を対象とする統計解析の方法を総称して多変量解析という．多次元ベクトル値から少数の代表的な変数に情報を圧縮することを主眼とする主成分分析，データの判別や分類を目的とする判別分析（クラスター分析），ベクトル同士の相関分析を行う正準相関分析，あるいは潜在因子の探索を行う因子分析などがよく用いられる［長倉ほか : 1998］．頁岩の成分間の相互関係の解析などに用いられた例がある［Curtis : 1969］．

出典　朝倉書店

ブリタニカ国際大百科事典 小項目事典

多変量解析
たへんりょうかいせき
multivariate analysis

多次元解析ともいう。主として統計学の分野で用いられる手法で，得られた多くの変数の間にある相互の関連を考慮しながら，各変数に目的に応じた重みづけをし，結果として得られる合成得点を，複数の異なった分類軸の組合せによって多次元空間に位置づける分析手法。特に，コンピュータ処理のプログラミングにおいて，多くの統計情報の計算に利用する場合の手法をさす。複雑そうにみえる事象の多くの情報から有用な情報のみを取出し，問題の解決をはかることを目的とする。重回帰分析，クラスター分析，因子分析など多くの技法があり，工学，社会学，経済学，政治学，心理学などの分野でも用いられる。

出典　ブリタニカ国際大百科事典 小項目事典

ASCII.jpデジタル用語辞典

多変量解析

互いに関連する複数の要因から成る問題を、統計的に分析する方法の総称。クラスタ分析、因子分析などの方法がある。経済学や心理学など、あらゆる分野で利用されている。

出典　ASCII.jpデジタル用語辞典

栄養・生化学辞典

多変量解析

　関連する多数の測定データを統計的に解析し，影響する変動要因の程度などを見つけだす方法．

出典　朝倉書店

ブランド用語集

多変量解析

多変量解析とは複数の変数を同時に分析する統計分析手法の総称のことをいう。

出典　(株)トライベック・ブランド戦略研究所