代数体の整数論（読み）だいすうたいのせいすうろん

改訂新版　世界大百科事典

代数体の整数論 (だいすうたいのせいすうろん)

有理数を係数とする代数方程式の根となりうる複素数を代数的数といい，その数が満たす有理数係数の既約な方程式の次数をその代数的数の次数という。例えば，\(\sqrt{5}\)は二次の代数的数である。有理数全体をQで表すことにする。有限個の代数的数をQに添加して得られる体を有限次代数体，または単に代数体という。代数体は，適当な1個の代数的数θを添加したQ（θ）の形で与えられる。このような代数体においてもQにおけると同様，整数やその間の整除という関係が定められ，整数論を考えることができる。これを代数体の整数論という。代数体の整数論は，C.F.ガウスが4乗剰余の研究の中でガウス数体と呼ばれる体Q（i）（iは虚数単位）における整数論を考えたことに始まる。その後，E.E.クンマーによる円分体の研究や，J.W.デデキントによるイデアルの理論などによって形が整えられ，D.ヒルベルトの報文《Zahlbericht》においてその基礎が確立した。またヒルベルトが提出した類体論の構想は，その後の代数体の発展に重要な役割を果たした。

代数体

代数体K＝Q（θ）において，θの次数を代数体Kの次数といい，［K：Q］で表す。［K：Q］＝nとすれば，Kの元αは一意的に，

　α＝a₀＋a₁θ＋……＋a_n-1θⁿ⁻¹　（a_iは有理数）　

の形に表される。θの満たす既約方程式の根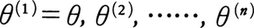，をθの共役といい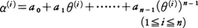，をαの共役という。また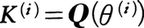をKに共役な体という。αに対して，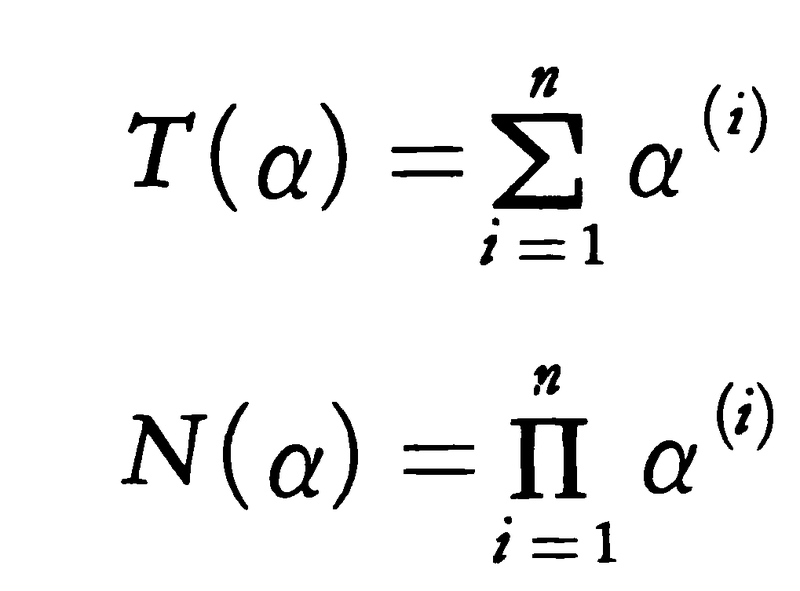

をそれぞれ，αのトレースtrace，ノルムnormという。

　代数体の重要な例として，二次体，円分体がある。一般に1の原始m乗根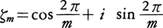，をQに添加して得られる体を円分体cyclotomic fieldという。mが素数pのとき，

　X^p⁻¹＋X^p⁻²＋……＋X＋1

は既約な多項式だから，［Q（ζ_p-1）：Q］＝p－1である。一般のmに対しては，オイラーの関数をφとして，［Q（ζ_m）：Q］＝φ（m）である。二次体については〈二次体の整数論〉の項を参されたい。

代数的整数

最高次の係数が1である整数係数の代数方程式の根となりうる複素数を代数的整数，または単に整数という。通常の整数を代数的整数と区別するために，有理整数ということがある。以下，代数的整数を単に整数ということにする。上で考えたζ_mは整数である。α，βが整数ならば，α±β，αβも整数である。したがって，代数体Kに含まれる整数全体をOで表すと，Oは単位元1を含む環であり，これをKの主整数環，または整数環という。［K：Q］＝nとすると，Oの元ω₁，……，ω_nが存在して，Oの元は，

　a₁ω₁＋a₂ω₂＋……＋a_nω_n　（a_iは有理整数）　

の形で表される。ω₁，……，ω_nをOの底，基，最小基などという。底ω₁，……，ω_nおよびそれらの共役を成分とする行列式，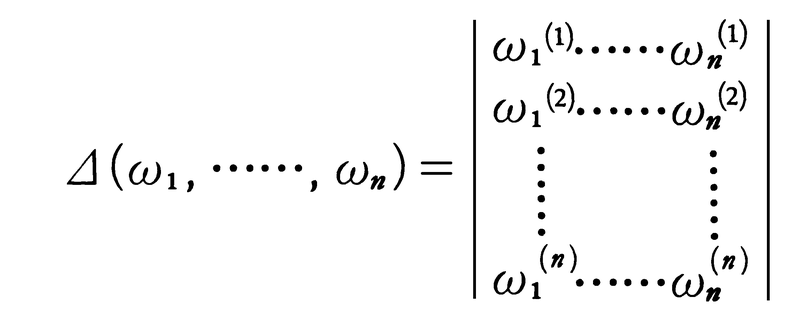

を考えると，その平方D_k＝⊿（ω₁，……，ω_n）²は底の取り方によらない。これをKの判別式という。

　二つの整数α，βに対して，α/βが整数であるとき，αはβで整除される，または割りきれるといい，αをβの倍数，βをαの約数であるという。

イデアル

代数体の整数環においては，素因数分解の一意性はもはや成り立たない。この困難を克服するために，イデアルが考えられた。O，｛o｝と異なるイデアル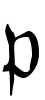で，x，y∈Oに対し，

　xy∈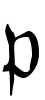ならば，x∈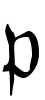またはy∈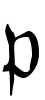

が成り立つものを素イデアルという。O，｛o｝と異なるイデアルは素イデアル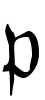₁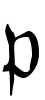，……，_nにより一意的に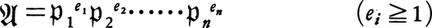，と分解される。

　二つの整数α，βに対しα－βがイデアルに含まれるとき，αとβはを法として合同であるといい，

　α≡β　（mod　）

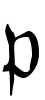と記す。Oをを法として合同なものを同じ組に属するとして分けると，有限個の類に分かれるが，その個数をのノルムといいN（）で表す。このとき素イデアルに対して，フェルマーの定理の拡張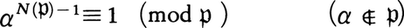，が成り立つ。またN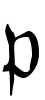（）は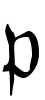に含まれる素数pのべきp^fとかける。このfを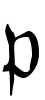の次数という。

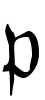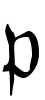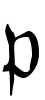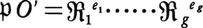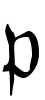　K′がKを含む代数体，O′がK′の整数環であるとき，Kの素イデアルに対して，O′は必ずしも素イデアルではない。O′のO′での素イデアルによる分解を，と表すときに，e_iを分岐指数という。N（_i）はN（）のべき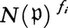となる。f_iを_iの相対次数という。とくにe₁＝e₂＝……＝e_n＝1のとき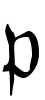は拡大K′/Kで不分岐であるといい，すべてのKの素イデアルが不分岐であるときK′/Kは不分岐拡大であるという。

　二つのイデアル，に対しKの0と異なる元αで＝αとなるものが存在するとき，とは同じ組に属するとして，（0）以外のイデアルを類別すると有限個の類に分かれる。これらの類の個数をKの類数という。またこれらの類は，イデアルの積により，有限アーベル群をなす。これをイデアル類群という。

単数

Oの元αに対し，α⁻¹もOに含まれるときαはKの単数であるという。Kと共役な体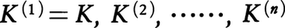の中で実数全体に含まれるものの個数をr₁，それ以外のものの個数を2r₂とすれば，Kにはr＝r₁＋r₂－1個の単数ε₁，……，ε_rが存在して，任意の単数は一意的に，の形に表される。ρはKに含まれる1のべき根である。これをディリクレの単数定理という。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の代数体の整数論の言及

【整数論】より

…その後ガウスは4乗剰余の相互法則の研究を始め，そのためにガウス数体と呼ばれる二次体の整数論を展開した。これが代数体の整数論の出発点となった。この4乗剰余の相互法則の研究は，一般のnべき剰余の相互法則の研究として，アイゼンシュタイン，E.E.クンマーらに受け継がれて，D.ヒルベルトによる類体論の構想の中に組み入れられた。…

※「代数体の整数論」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」