作用量子（読み）さようりょうし

精選版 日本国語大辞典

さよう‐りょうし‥リャウシ【作用量子】

1. 〘 名詞 〙 量子力学の定数で、作用量の最小単位と考えられたもの。プランクの定数ｈで表わす。→プランクの定数

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

作用量子
さようりょうし

物理量のなかにエネルギーと時間、あるいは座標と運動量との積の次元を有する作用量とよぶものがある。量子力学では、この量が連続的な値をとらずとびとびの値をとり、基本量の整数倍となっている。この基本量としての作用量を作用量子といい、プランク定数hで表す。

　作用量は力学理論の基本的な量であって、古典力学では運動量pと座標の時間に関する微分係数との積を運動開始と終了の間で積分したものであり、この量が最小の値をとる軌道が現実に粒子がとる軌道である。

　ボーアは、水素原子内電子の運動状態として可能なものは、その軌道で求めた作用量がプランク定数hの整数倍に限られるという条件を与えた。いま、電子が半径rの円運動を行っているとすれば、運動量はmv²/r＝e²/r²から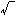(me²/r)（eは単位電荷、mは電子の質量）、作用はこれに円周を乗じた2πr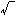(me²/r)となる。このとき、ボーアの量子条件は2πr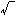(me²/r)＝nhとなって、許される電子の軌道の半径はr＝n²ħ²/me²で与えられる(ħ＝h/2π)。ħ²/me²をボーア半径という。

　運動量や座標のかわりに力学系を論ずる場合の変数、すなわち力学変数として作用量を用いることもある。これを作用変数という。作用量が量子力学の誕生にきわめて重要な役割を果たしたのは、この量が断熱不変量であって、作用量の満たす関係式がしばしば古典論と量子力学とで同じ形式をもつためであると考えられる。

［田中　一］

[参照項目] | 運動量 | 断熱仮説 | 電荷 | プランク定数 | ボーア

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

作用量子
さようりょうし
quantum of action

プランク定数 h の別名。1900年 M.プランクは実験とよく合う熱放射式を半経験的な内挿式として求めたが，すぐあとに，振動数 ν の熱放射線はエネルギー hν の塊として放出されるという量子仮説に基づいてこの式を導き出した。定数 h は作用量の次元 (エネルギー × 時間) をもつので，前期量子論では作用量子と呼ばれた。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

作用量子【さようりょうし】

→プランク定数

出典　株式会社平凡社

世界大百科事典（旧版）内の作用量子の言及

【作用量】より

…n＝0,1,2，……，0≦α/4＜1,αのことをマスロフの指数と呼ぶ)でなければならないという命題によって，この力学系の量子条件が提出された。定数hが作用量子という名称で呼ばれる理由でもある。前述の閉軌道の面積を閉軌道に沿う積分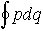で表し，これをこの力学系を記述する作用変数と呼び，ふつうJという記号で表す。…

【プランク定数】より

…hで表され，その値は，　h＝6.626076×10^－34J･sである。その次元(エネルギー)×(時間)は，また(運動量)×(長さ)などとも書け，一般に作用の次元と呼ばれるので，hを作用量子ともいう。原子内の電子のエネルギーEは10^－17Jの程度で公転時間tは10^－16sの程度だから，その積Etはhの程度になる。…

【量子】より

…ここにhはプランクの定数，cは光速度である。プランク定数が作用量子とも呼ばれるのは，量子力学の前身である古典量子論において，量子条件を〈作用量積分がhの整数倍〉とした歴史による。振動数νの放射のエネルギーをhνの整数倍としたのはプランクの放射則の含意をさぐったM.プランク自身であるが(1900)，hνを量子と呼んだのは1909年のプランクからH.A.ローレンツへの手紙が最初である。…

※「作用量子」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」