運動量（読み）ウンドウリョウ

デジタル大辞泉

うんどう‐りょう〔‐リヤウ〕【運動量】

１ からだを動かす度合い。
２ 物体の運動の激しさを示す量。物体の質量と速度との積で表される。

出典　小学館

精選版 日本国語大辞典

うんどう‐りょう‥リャウ【運動量】

1. 〘 名詞 〙
2. ① 物体の質量と速度との相乗積で表わされるベクトル量で、運動の激しさを表わす。物体の運動量の時間的変化の割合はそれに働く力に等しい。また、物体に力が働かないときは運動量の大きさは変わらない。〔物理学術語和英仏独対訳字書（1888）〕
3. ② 人や動物が運動する量。
   1. [初出の実例]「運動量の少ない肥った虫が」(出典：無明長夜（1970）〈吉田知子〉二)

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

運動量
うんどうりょう

物体の運動を量として表したもので、質量mの物体が速度vで運動しているとき、mvをこの物体の運動量という。運動量のことを線運動量ということがある。この名称は角運動量と区別するための名称であるが、一般にはあまり用いられない。

　速度vの大きさが光の速さに近い場合には、運動量pは、静止質量m₀を用いて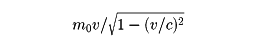

で与えられる（cは光速）。質点の集まり、すなわち質点系の運動量は、各質点の運動量の和である。一般の物体の運動量は、これを微小部分に分けたときの各部分の運動量の総和で与えられる。

［田中　一・加藤幾芳］

物理量としての運動量

運動の量として運動量を導入したのはデカルトであるといわれているが、当時は、運動量と、今日われわれが運動エネルギーとよんでいる物理量とを区別せず、混同することが多かった。しかし運動量はベクトル量であり、これに対し運動エネルギーはスカラー量で、互いに異なる物理量である。

　ニュートンの運動の第二法則によれば、質点の運動量の時間的変化は外力に等しい。第二法則のこの形は、個々の質点の属性には無関係であり、質点が外力の作用を受けたときに生じる状態の変化は運動量の変化であって、加速度は質点の属性である質量に依存し、運動量の変化を質量で割って得られることを示している。質量が運動とともに変化する場合にも、運動量の時間的変化が外力に等しい。たとえば、電場の強さE、磁場の強さHの作用を受ける荷電qの粒子の相対論的な運動方程式は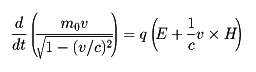

で与えられる。以上のことは、運動量が物体の運動において基本的な役割を果たしていることを示す。

　一般の力学系を解く場合、この力学系を構成する粒子の位置座標rを用いるのが、かならずしも効果的であるとは限らない。たとえば太陽系においては、極座標を用い、太陽と惑星との間の距離rや惑星の回転角θを用いたほうが、惑星の運動の特徴をよく表現することができる。この場合、運動量に相当する物理量p_r、p_θをrやθに対して定義することができる。さらに拡張して、力学系を記述する一つの量qに対する運動量pを導入することができる。それには、力学系の運動エネルギーTやポテンシャルエネルギーV（位置エネルギー）を、qと、qの時間に関する微係数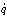で表す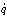（＝dq/dt）。運動量pは、qと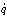の関数としてのTとVの差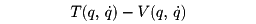

で微分すればよい。すなわち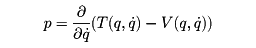

である。qを通常の位置座標xとすれば、Vはもともと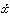を含まないので、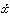に関するVの微係数はゼロとなり、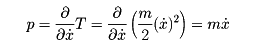

となって、この一般的な運動量の定義が、通常の運動量の定義を特別の場合として含んでいることがわかる。qとpを、拡張された座標と運動量という。このqとpとで書き直した運動方程式はqとpとを－pとqとに置き換えてもまったく同じ形式になる。このことは、qとpという物理量が互いに入れ換え可能な、つまり共役(きょうやく)の関係にあることを示している。qとpとを正準共役な力学変数という。正準共役な力学変数は、古典力学のみならず量子力学においても核心的な役割を担っている。

［田中　一］

さまざまな場合の運動量

ニュートンの運動の第三法則は、物体Aが物体Bに作用を及ぼしているとき、同時に物体Bは物体Aに同じ大きさで方向が逆の作用、すなわち反作用を及ぼすことを示している。作用が運動量の変化率であったから、結局は物体Aと物体Bがそれぞれ相互の作用によって得る運動量の変化が打ち消されてしまう。このように力学系の全運動量pは、力学系内の物体間の相互作用では変化しないので、この力学系に作用する全外力をFとすればdp/dt＝Fとなる。したがって、外力がなければ力学系の全運動量は保存される（変化しない）。これを運動量保存の法則という。たとえば、相互作用する2粒子間の衝突の場合、その全運動量は保存される。相対性理論では、粒子のエネルギーEは、その静止質量m₀と運動量pの間にE²＝c²p²＋m²c⁴の関係がある。このときEとcpとは四次元ベクトルを構成する。量子論によれば光は粒子性をもち、このときの光の粒子すなわち光子のエネルギーは、光の振動数をνとしてhνで与えられる（E＝hν。hはプランク定数）。光子の静止質量はゼロであるから、その運動量はhν/cとなり、あるいは、波長λを用いればh/λとなる。量子論における物理量には演算子が対応している。

　粒子の位置座標をxなどとすれば、運動量の演算子は

などで与えられる。量子的状態がとる運動量の値とその状態は、演算子の固有値と固有状態となる。たとえば、x方向の運動量の値をp'_xとすれば、固有状態∅は、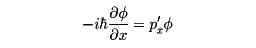

となって、∅は、波長λがλ＝h/p'_xの波を表す関数となる。このように、運動量pの粒子には波長h/pの波動が伴っている。水素原子内電子の場合、この波長は、水素原子の広がり5×10^-11メートルの程度である。

［田中　一・加藤幾芳］

[参照項目] | 演算子 | スカラー | プランク定数 | ベクトル

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

運動量 (うんどうりょう)
momentum

物体の速度ベクトルvとその質量mとの積mv＝pで表されるベクトルpを物体の運動量と呼ぶ。運動量は運動している物体に固有な一つの性質（いきおいとでもいうべきもの）を示す量であって，これの大きいものほど止めるのに大きな力を要する。しかもこの量は二つの物体の衝突の際，やりとりがあっても総和はその前後で変わらない（保存される）。R.デカルトはこの理由で多様な運動の中で運動量（彼自身quantité demouvementと呼んだ）こそが保存される量であると考え，宇宙の全運動量は保存されると主張した。この立場からデカルトやその支持者は，運動の原因としての力や運動の変化は，運動量の変化（または変化率）で測ることができると考えた。ニュートンの運動方程式は確かに運動量を用いて，物体の運動量の時間的変化率はこれに働く力（これもベクトルとしてFで表す）に等しいといい表すことができる。非常に短い時間⊿tの間に大きな力Fが加わって有限の運動量の変化⊿pが生ずるときには，上述の関係を，運動量の変化高⊿pは力積F⊿tに等しいという形に表すこともできる。二つの物体A，Bがお互いに力を及ぼしあっているが，それ以外の力を受けないで運動している場合，全運動量 p_A＋p_Bは時間的に一定で変化しない（保存される）。これは運動量保存則あるいは運動量保存の法則と呼ばれている。全運動量 p_A＋p_Bを考えるとき，お互いに及ぼしあっている力は，作用と反作用として打ち消しあい，その時間変化を引き起こさないからである。

　質量をもつ粒子の運動量は上のように定義されるが，質量をもたない電磁場，具体的には光も運動量をもつことが知られている。実際，振動数νの光がその進行方向にhν/c（hはプランク定数，cは光速）の運動量をもつことは，光と電子の衝突（光のコンプトン散乱）での運動量の保存を通じて確かめられている。一般に電磁場を通じて相互に力を及ぼしあっている粒子の場合には，運動量保存則も電磁場の運動量まで考えに入れてはじめて成立する。相対論では，運動量pとE/c（Eはエネルギー）をひとまとめにして四元運動量として扱い，外力の働いていない粒子の衝突では，それらの粒子の四元運動量の和が保存される（四元ベクトル）。量子力学では運動量は波動関数に対する演算子で表され，位置座標をx，y，zとするとき，例えば運動量のx成分は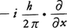となる。量子力学での運動量の保存は体系の並進操作に対する不変性と結びついている。
執筆者：田辺 行人

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

運動量
うんどうりょう
momentum

質点の質量 m と速度 v との積で定義されるベクトル量 p＝mv を運動量という。角運動量と区別して線運動量とも呼ばれる。ニュートンの運動方程式は，運動量の時間変化率が物体に働く力 f に等しい（dp/dt＝f）とも表わされ，この形の運動方程式は非常に高速な運動に対する相対論的力学でも正しく成り立つ。質点系（質点の集団）の運動量は，各質点の運動量のベクトル和で与えられている。大きさのある物体の運動量 P は，質量と重心の速度との積で与えられる。質点系や物体の運動量 P の時間変化は外から加わる外力 F だけで決まり，dP/dt＝F であって，質点の場合とまったく同形となる。解析力学では一般運動量p_i が考えられ，量子力学では p_i は座標 x_i についての微分演算子 －iℏ∂/∂x_i で表わされる。ここで ℏ は h/2π（h はプランク定数）である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

運動量【うんどうりょう】

物体の質量と速度の積。運動方向に向かうベクトルで表され，幾つかの物体の全運動量は各物体の運動量のベクトル和となる。運動量の時間的変化の割合は，それに働く力に等しく，またある時間の間に生じた運動量の変化は，その間に作用した力積に等しい。
→関連項目位相空間（物理）｜運動量保存の法則

出典　株式会社平凡社

世界大百科事典（旧版）内の運動量の言及

【エネルギー】より

…彼は1600年ごろ，木材の上に立てた釘の頭に金づちの頭よりずっと重い物を載せても釘は木の中に入らないが，金づちを振り上げて打つだけでなぜ釘は楽に木材に打ち込まれるのかを問題にし，運動する物体には何か固有の“ちから”があると考えた。これについてR.デカルトは44年の著書で，衝突現象で運動量mv(mは物体の質量，vは物体の速度)が保存されることに注意し，全宇宙における総運動量が不変であり，運動量こそが運動する物体のもつ“ちから”であると主張した。デカルトやその支持者たちの考え方からすると，運動や運動の変化の原因としての(外から働く)力は運動量の変化として測られることになる。…

※「運動量」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」