精選版 日本国語大辞典 「慣性モーメント」の意味・読み・例文・類語
かんせい‐モーメントクヮンセイ‥【慣性モーメント】
改訂新版 世界大百科事典 「慣性モーメント」の意味・わかりやすい解説
慣性モーメント (かんせいモーメント)
moment of inertia
傘を心棒のまわりで回転させたりとめたりするときの手ごたえは,傘を開いているときとたたんでいるときとで異なる。開いているときのほうが回転させたりとめたりするのに大きな力を要する。この例のように回転をさせたりとめたりするときの手ごたえの大小,言い換えれば回転運動に対する抵抗の大小を表す量が慣性モーメントである。慣性モーメントが大きいものほど回転の状態(静止から回転を始める場合も含めて)を変化させるのに大きな力を要する。以下,物体としては剛体を考える。物体を細かく分けたと考え,それぞれの細片の質量をm1,m2,……,それぞれの細片と回転軸との距離をr1,r2,……とするとき,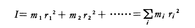 で表される量Iのことを,その軸のまわりの慣性モーメントという。物体がその軸のまわりで角速度ωで回転しているとき,細片の速さはriωであるから,物体の運動エネルギーKは,
で表される量Iのことを,その軸のまわりの慣性モーメントという。物体がその軸のまわりで角速度ωで回転しているとき,細片の速さはriωであるから,物体の運動エネルギーKは,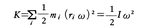 と表される。モーメントがNの力でωを変化させる場合を考えると,微小角⊿θだけ回転する間(時間は⊿t=⊿θ/ω)に力のする仕事はN⊿θで与えられるので,これを運動エネルギーの増加に等しいとおいて,
と表される。モーメントがNの力でωを変化させる場合を考えると,微小角⊿θだけ回転する間(時間は⊿t=⊿θ/ω)に力のする仕事はN⊿θで与えられるので,これを運動エネルギーの増加に等しいとおいて,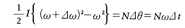 から,⊿t→0の極限で,
から,⊿t→0の極限で, が得られる。これはd(Iω)/dt=Nとかいても同じである。これらの式を,質量mの物体が力Fを受けて速度Vを変化させる場合の,
が得られる。これはd(Iω)/dt=Nとかいても同じである。これらの式を,質量mの物体が力Fを受けて速度Vを変化させる場合の,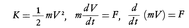 と対応させることができ,並進運動の慣性を表す質量に対応するのが回転の場合の慣性モーメントであることがわかる。運動量mVに対応するのは角運動量Iωである。なお,回転軸からの距離rにおける密度ρが与えられるような連続物体では,慣性モーメントは
と対応させることができ,並進運動の慣性を表す質量に対応するのが回転の場合の慣性モーメントであることがわかる。運動量mVに対応するのは角運動量Iωである。なお,回転軸からの距離rにおける密度ρが与えられるような連続物体では,慣性モーメントは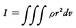 で与えられる。
で与えられる。
物体の重心を通る軸のまわりの慣性モーメントをI0,その軸に平行でdだけ離れた軸のまわりの慣性モーメントをIとすると,I=I0+Md2という関係がある。Mは物体の質量で,この関係を平行軸の定理という。I=Mκ2とおいてκを回転半径と呼ぶこともある。半径aの一様な球の直径のまわりの回転半径は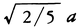 に,接線のまわりの回転半径は
に,接線のまわりの回転半径は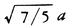 に等しい。
に等しい。
執筆者:小出 昭一郎
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「慣性モーメント」の意味・わかりやすい解説
慣性モーメント
かんせいもーめんと
質点系の各質点の質量mに、ある一定直線までのそれぞれの距離rの2乗を掛けて全部について加えた量Σmiri2を、その直線に関する質点系の慣性モーメントという。剛体の場合は微小部分に分け、各部分の質量dmに距離rの2乗を掛け、全体に対して積分することによって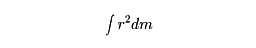
で与えられる。したがって慣性モーメントは、質量が大きく、かつ回転軸から遠くに分布するほど大きくなる。
直角座標系の原点を通る一定直線(方向余弦λ、μ、ν)に関する剛体の慣性モーメントIは
I=λ2Ixx+μ2Iyy+ν2Izz-2λμIxy
-2μνIyz-2νλIzx
である。ただし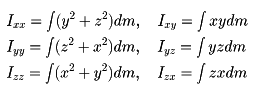
Ιxx、Ιyy、Ιzzをそれぞれx、y、z軸に関する慣性モーメント、Ixy、Iyz、Izxを慣性乗積という。適当な方向に直角座標軸を選ぶと慣性乗積が三つともゼロとなる。この場合の座標軸を慣性の主軸といい、Ixx、Iyy、Izzを主慣性モーメントとよぶ。
ある直線に関する物体の慣性モーメントIをその全質量Mで割ったk2=I/Mより定められるkを回転半径という。すなわち、物体は質量Mの一つの質点が回転軸からkの距離にあると同じ慣性モーメントをもつことになる。また物体の重心を通る軸に関する慣性モーメントをIgとすると、その軸からdだけ離れた平行軸に関する慣性モーメントIはI=Ig+Md2で与えられ、これを平行軸の定理という。
[村岡光男]
百科事典マイペディア 「慣性モーメント」の意味・わかりやすい解説
慣性モーメント【かんせいモーメント】
→関連項目運動の法則|角運動量|実体振子|てんぷ|はずみ車
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「慣性モーメント」の意味・わかりやすい解説
慣性モーメント
かんせいモーメント
moment of inertia
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
化学辞典 第2版 「慣性モーメント」の解説
慣性モーメント
カンセイモーメント
moment of inertia
慣性能率ともいう.質量mの質点からある直線までの距離をrとするとき,mr 2をこの直線に対するこの質点の慣性モーメントという.剛体のときは,剛体を微小部分に細分化し,それぞれの微小部分についての和,Σimiri2がこの剛体の直線に対する慣性モーメントになる.質点や剛体の関係する力学の議論に必要になる.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
栄養・生化学辞典 「慣性モーメント」の解説
慣性モーメント
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


