角運動量（読み）カクウンドウリョウ

デジタル大辞泉

かく‐うんどうりょう〔‐ウンドウリヤウ〕【角運動量】

回転運動の特徴を表す基本量。質点では、原点からの位置ベクトルと運動量ベクトルとの外積で、運動量のモーメントに相当する。

出典　小学館

精選版 日本国語大辞典

かく‐うんどうりょう‥ウンドウリャウ【角運動量】

1. 〘 名詞 〙 回転の勢いを表わす物理量。回転物体の各部の速さとその部分の質量との積（運動量）に、回転中心からその速度に垂直にひいた垂線の長さ（腕の長さ）をかけた積を回転する物体全体にわたって加え合わせた量で表わす。こまの角運動量は回転速度が大きいほど、また、質量が回転軸から遠い周辺に集中しているほど大きい。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

角運動量
かくうんどうりょう

物体の回転の大きさを表す、3成分をもつベクトル量。粒子の位置をx、y、z、運動量をp_x、p_y、p_zとすれば、角運動量はそのx、y、z方向の成分が
　yp_z－zp_y, zp_x－xp_z, xp_y－yp_x
で与えられる。複数の粒子系の角運動量は各粒子の角運動量を成分ごとに総和したものであり、連続的な広がりをもつ物体の角運動量は、この物体を小さな部分に分けたときの各部分の角運動量の総和である。

　粒子の位置ベクトルをr、運動量ベクトルをpとすれば角運動量Lは、前述の定義が示すように、rとpとのベクトル積r×pとなる。この形は、角運動量が運動量のモーメントであることを示している。またrの原点が変わればLの値も変わってくる。

［田中　一］

マクロな運動における角運動量

マクロな運動の場合、角運動量は面積速度に粒子の質量mの2倍を乗じたものである。いま粒子が半径aの円周上を一定の速さで回転しているとする。このとき円の中心と粒子とを結ぶ半径は、2πa/vの時間にπa²の面積を掃過(そうか)する（描く）。このとき面積速度は、大きさが
　πa²÷(2πa/v)＝va/2
で、その方向が図Aの示す線分で表現される量である。この場合、角運動もまた同じ方向をもち、大きさが面積速度の2m倍、すなわちmvaの線分で表すことができる。

　粒子に力が働くと、角運動量は一般には変化するが、力は直接なままの形では作用せず、力をベクトルfで表すと、力のモーメントr×fの形で作用する。したがって、角運動量の運動方程式はdL/dt＝r×fとなる。粒子に働く力が中心力の場合には、力の中心に関する力のモーメントはつねにゼロとなって、角運動量は時間的に変化せず保存される（角運動量の保存則）。

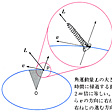
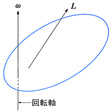
　剛体の場合には、各部分に働く力のモーメントの和をNとすれば、その角運動量Lの時間的変化は、dL/dt＝Nで与えられる。剛体は内部変化を行わない物体であるので、その運動状態を少数個の物理量で表現することができる。たとえば、剛体がある固定した軸の周りを回転する場合の各運動量と力のモーメントは、軸方向の成分L_z、N_zのみをもち、その時間変化はI(dL_z/dt)＝N_zで与えられる。ここでIは、ニュートンの運動方程式の質量に相当する量で、剛体の密度分布と回転軸の位置から定まり、慣性モーメントという。注意すべきことは、剛体内の密度分布が回転軸の周りに対称でない場合、一般に角運動量Lの方向と回転軸ωの方向とが異なることである（図B）。この場合にも、角速度をωとすれば、L＝Iωの関係があるが、Iは単なる数ではなく剛体の密度分布から決まるテンソルであって、これを慣性テンソルという。なお、これらの角運動の方程式は、いずれもニュートンの法則から導かれるものである。

［田中　一］

量子的な運動における角運動量

量子的な運動の場合、物理量はつねに演算子として表現されており、その値はこれらの演算子の固有値で与えられている。軌道運動の角運動量の演算子は、運動量の演算子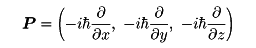

を用いて、L＝r×pすなわち、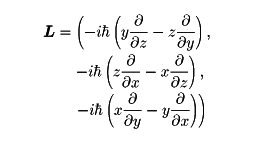

となる。ここでħは、プランク定数hを2πで割ったものである。量子的な運動における軌道角運動量のとる値は、マクロな運動（古典力学的運動）の場合と、次の3点で著しく異なっている。(1)角運動量のどの2成分もそれらの値が同時に決まることはない。(2)角運動量の大きさといずれか一つの成分のみその値を同時に決めることができる。(3)この場合角運動の大きさとその1成分のとる値は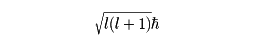

およびmħの値のみである。ここで、lは0または正の整数であり、mには1個のlに対して2l＋1個の選び方があって－l≦m≦lを満たす任意の整数である。このように角運動量を量子的に扱うことを角運動量の量子化という。

　量子的状態の場合でも角運動が保存されることが多い。この場合、量子的状態はlとmとで表すことができる。lとmを角運動量の量子数という。lの値ごとに、表で示すようなアルファベットの文字を用いて量子的状態を表すことが多い。

　電子や陽子、中性子あるいは光子などの素粒子は自分自身の角運動量を有している。この場合の角運動量は、粒子が広がりをもたなくても現れるものであって、その意味で粒子の自転運動に由来するものではなく、これらの粒子を表現する波動関数の成分の数で決まる。これをスピン角運動量といい、その値は前述の軌道角運動量と同じ形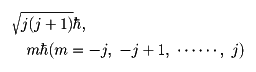

で与えられるが、jは粒子を表す成分の数をsとしてj＝(s－1)/2となる。電子や陽子の場合sが2であって、j＝1/2となる。一般にjは整数か半整数（整数に1/2を加えたもの）となる。したがって、軌道角運動量の場合も含めて、角運動の大きさとその1成分の値は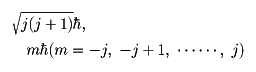

となる。

　2個あるいはこれ以上の角運動量の和を合成角運動量という。合成角運動量のとる値も1個の角運動量の場合と同様であって、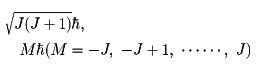

　で与えられる。j₁、m₁、j₂、m₂の二つの角運動量を合成した場合には、Jは
　　j₁＋j₂，j₁＋j₂－1，……，|j₁－j₂|
のいずれかである。この場合の合成角運動量の固有状態は、M＝m₁＋m₂を満たすm₁とm₂との組を重ね合わせて得ることができる。

［田中　一］

自然現象と角運動量

太陽系の惑星の運動、とくに火星の運動を観測して、ケプラーとティコ・ブラーエは、惑星の面積速度が一定であることを発見した（ケプラーの第二法則）。これは惑星運動の角運動量保存を観測したものといえよう。また、太陽系ではその軌道がほぼ同一面内にあって、各惑星の回転の向きは同じである。これは各惑星の角運動量が同じ方向を向いていることを示している。太陽系全体の角運動量は各惑星が担っているとみてよい。

　原子や原子核の状態は、角運動量の大きさとその1成分の固有状態になっていることが多く、しかもその値はあまり大きくないのが普通である。このため、核反応や核の崩壊現象を研究するうえで、角運動量の保存則はきわめて有効である。

［田中　一］

[参照項目] | 運動量 | ケプラー | ケプラーの法則 | 剛体 | ティコ・ブラーエ | モーメント

角運動量〔図A〕

角運動量と角速度〔図B〕

角運動量の固有状態の記号〔表〕

出典　小学館　日本大百科全書(ニッポニカ)

化学辞典 第2版

角運動量
カクウンドウリョウ
angular momentum

特別な定点 r₀ のまわりを動く質点の運動が r₀ を通る一平面内に限られているとき，r₀ を座標系の原点にとり，その平面をxy面にとることができる．いま，r₀ に関する質点の運動量ベクトルp(p_x,p_y,p_z ＝ 0)のモーメントLを考えると，その3成分中 L_x，L_y は

L_x ＝ L_y ＝ 0
であり，

L_z ＝ xp_y － yp_x
である．以下，この L_z の意味を調べるため質点の質量をmとし，その速度をv(v_x,v_y,v_z ＝ 0)とすると，

p ＝ mv
であり，

p_y ＝ mv_y，p_x ＝ mv_x
であるから，

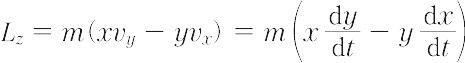
となる．ここで，(x,y)座標から極座標(r,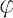)に座標変換を行うと，

x ＝ r cos 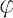，y ＝ r sin ，

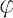dx/dt 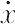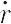＝ ＝ cos 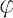－ r sin ･，

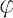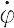dy/dt 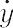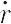＝ ＝ sin 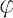＋ r cos ･
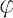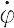
であるから

L_z ＝ mr ²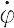
である．一方，この場合の質点の運動のエネルギーTを(r,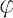)座標で表すと，

T ＝ (m/2){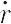² ＋ (r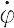)²}
であり，

L_z ＝ mr ²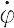 ＝ ∂T/∂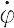
の関係にある．これは，

L_z ＝ mr ²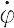
が一般化座標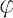に共役な運動量，すなわち，角運動量であることを示す．このように運動量のモーメント，すなわち，能率が角運動量である．

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

角運動量
かくうんどうりょう
angular momentum

(1) 物体の回転運動の大きさを表わす量。質点が位置ベクトルr の点で運動量 p をもつとき，原点に関する運動量のモーメント r×p を角運動量 l という。力 F が働くとき，角運動量の時間変化率は原点に関する力のモーメントに等しく，dl/dt＝r×F である。質点系の角運動量は構成質点の角運動量のベクトル和で与えられる。ある軸のまわりを角速度ωで回転する剛体では，その軸のまわりの慣性モーメントを I とすれば，角運動量は Iωとなる。ある点のまわりの剛体の回転では，角速度ベクトルをω＝（ω_x，ω_y，ω_z），慣性テンソルを I＝（I_xx，I_xy，…）とすれば，剛体の角運動量は成分 I_xxω_x＋I_xyω_y＋I_xzω_z，I_yxω_x＋I_yyω_y＋I_yzω_z，I_zxω_x＋I_zyω_y＋I_zzω_z をもつベクトルで与えられる。
(2) 量子力学では，運動量 p を微分演算子 －iℏ▽で置き換えて，r×（－iℏ▽）を軌道角運動量 l という。ただし ℏ＝h/2π，h はプランク定数，また▽は偏微分∂/∂x，∂/∂y，∂/∂z を成分とするベクトルである。したがってベクトル l の成分は次の式で与えられる。
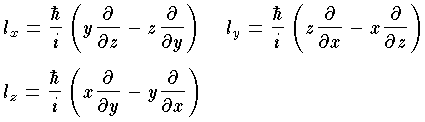電子や陽子などの量子力学的な粒子はスピン s と呼ばれる固有の角運動量をもち，これらのベクトル和 l＋s を全角運動量という。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

角運動量 (かくうんどうりょう)
angular momentum

物体の運動は並進運動と回転（運動）に大別される。並進運動に慣性があるように回転にも一種の慣性があり，摩擦がなければこまはいつまでも回転を続ける。並進運動の“勢い”を表す運動量P（質量m_iと速度V_iの積を物体全体で合計したベクトル量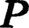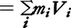：）に対応して回転の勢いを表すのが角運動量Lである。Lは物体の各部分がもつ運動量のモーメントの和，L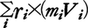＝で定義される（rは回転軸からの位置ベクトル）。固定軸のまわりを角速度ωで回転している場合なら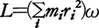， と表される。運動量の変化を引き起こすのが外力（の合力）であるのに対応して，角運動量の変化を起こすのは外力のモーメント（の和）であり，外力のモーメントが0ならば角運動量は一定に保たれる。これを角運動量保存則という。スケートのスピンではほぼそれに近くなっており，広げた手を縮めて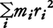（慣性モーメント）を小さくすると角速度ωが増加する。
執筆者：小出 昭一郎

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

角運動量【かくうんどうりょう】

任意の点から質点までの距離に，質点の運動量のその距離に垂直な成分を掛けた積を，その点のまわりの角運動量，または運動量のモーメントという。距離と運動量がきめる平面に垂直なベクトル，すなわち原点をO，質点の位置ベクトルをr，速度をv，質量をmとすると，r×mv（外積）で表される。質点系の角運動量は，各質点の角運動量のベクトル和に等しい。剛体の角運動量は，慣性モーメントと角速度の積になる。角運動量の時間的変化の割合は，外力のその点に関するモーメントに等しい。→角運動量保存の法則
→関連項目歳差運動｜スピン｜モーメント（物理）

出典　株式会社平凡社

世界大百科事典（旧版）内の角運動量の言及

【慣性モーメント】より

…これらの式を，質量mの物体が力Fを受けて速度Vを変化させる場合の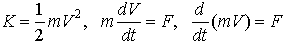，と対応させることができ，並進運動の慣性を表す質量に対応するのが回転の場合の慣性モーメントであることがわかる。運動量mVに対応するのは角運動量Iωである。なお，回転軸からの距離rにおける密度ρが与えられるような連続物体では，慣性モーメントは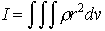で与えられる。…

【モーメント】より

…同様に，点Pでベクトル量Aが定められるとき，r×Aのことを，Oに関するAのモーメントという。例えば質点がPで運動量pをもっているとき，運動量のモーメントl＝r×pというものを考えることができるが，これを角運動量と名づけている。またモーメントはスカラー量にも用いることがある。…

※「角運動量」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」