翻訳｜friction
蘭学資料にみえるものが古く、漢籍には見えないところから、日本において、オランダ語の翻訳により、近世期に新たに生じた語と考えられる。
接触している二つの物体が相対的にすべりやころがり運動をするとき，あるいはしようとするときに，その接触面においてこれらの相対運動を妨げる方向の力が生ずる現象。この力を摩擦力というが，摩擦力を摩擦と略称することもある。運動がすべりの場合をすべり摩擦，ころがりの場合をころがり摩擦と呼び，単に摩擦といえばふつうは前者を指す。摩擦によって，力学的エネルギーが熱エネルギーに変換されるため，同様の変換が固体内部で行われる現象を内部摩擦というが，本項で述べる摩擦とは別の現象である。
摩擦は力学的エネルギーの損失をもたらすので，軸受や歯車などの機械要素をはじめ，接触面では摩擦の小さいほうが望ましいのがふつうであり，そのために潤滑が行われることが多い。しかし自動車のタイヤ，鉄道の車輪，あるいは摩擦伝動装置など，摩擦によって駆動力を得ているものもあり，ブレーキは摩擦によって力学的エネルギーを熱に変換することを目的とした装置である。身近な例でも，敷居やちょうつがいなど低摩擦の必要なものがある半面，靴と地面との間に摩擦がなければ歩けないし，繊維間の摩擦がなくなれば衣服はたちまちばらばらになってしまうだろう。
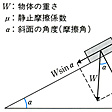
物体が接触面に垂直な力Pを受けて接触している場合を考える。まずすべり摩擦の場合（図1-a）には，接触面に平行な力Fを加えても，Fが小さいときには物体はすべり出さない。これは接触面に摩擦力F′が現れて，Fとつりあうためである。この力F′を静摩擦力または静止摩擦力という。静摩擦力には上限があって，fsPより大きくはなれない。このfsを静摩擦係数という。FがfsPより大きくなると物体はすべり始めるが，すべっているときにもF′＝fkPなる摩擦力が働く。これを動摩擦力といい，fkを動摩擦係数という。図1-bに斜面におけるすべり摩擦を示しておく。
次にころがり摩擦を考える。図1-cのように，物体が球，円筒あるいはそれに近い形をしている場合，それに接触面に平行な力Fを加えると，すべり摩擦の静摩擦力F′が存在するために，物体はころがり運動を始める。このとき接触部には，F″＝frPなるころがり摩擦力が働き，frをころがり摩擦係数という。通常F″はF′よりずっと小さい。
物体がすべりまたはころがり運動をしている場合の摩擦を運動摩擦ともいい，摩擦係数をf，すべりまたはころがりの速度をVとして，単位時間当りfPVに等しい力学的エネルギーが熱エネルギーに変換され，摩擦熱を発生する。
すべり摩擦の法則としては，次の三つが知られている。（1）摩擦力は接触面に垂直に加えられる力に比例し，物体間の見かけの接触面積とは無関係である，（2）動摩擦力はすべり速度には無関係である，（3）一般に静摩擦力は動摩擦力より大きい。このうち（1）と（2）は，1669年にフランスのアモントンGuillaume Amontons（1663-1705）が発表し，その後C.クーロンが確認したことから，アモントンの法則またはクーロンの法則と呼ばれている。前述した力学の説明にも（1）を用いたが，これらはもともと潤滑を行っていない面の摩擦について得られた経験則で，つねに厳密に成立するというものではない。
ころがり摩擦の場合には，摩擦力は垂直力にほぼ比例するが，ころがる物体の直径の－0.4乗から－1.7乗に比例するという測定例がある。ころがり速度の影響も無視できない。
実在する固体の表面には細かな凹凸があるのがふつうである。古くは摩擦の原因が，このような凹凸のかみあいに求められた。その要因もまったくないわけではないが，現在金属やプラスチックなど工業材料のすべり摩擦について，もっとも一般的な機構と考えられているのは，固体間の凝着とせん断である。固体の表面どうしを押し付けると，前述したように表面には細かな凹凸があるため，固体は見かけの表面全体で接触するわけではなく，実際の接触は図2のように限られた部分のみで起こる。そのような接触部を真実接触点といい，その面積を真実接触面積と呼ぶ。真実接触点1個の大きさは表面の状態によってさまざまであるが，大ざっぱな見当として，機械の摩擦面では0.01mm2以下の小さなものが多い。真実接触点は表面に垂直な力Pによるその付近の塑性流動によって生ずるのが一般で，いま固体の塑性流動を起こす圧力をpmとすると，真実接触面積Aは近似的にP/pmで表される。鋼の例をとるとpmは数百kgf/mm2であるから，Pが100kgfの場合を考えても真実接触面積は数分の1mm2にしかならない。真実接触点においては，二つの表面の原子あるいは分子が，それぞれの固体内部における原子間，分子間の距離と同程度まで近づくので，その間の相互作用によって凝着を生じ，界面が強度をもつようになる。接触した2面をすべらせるためには，このようにして強度をもった真実接触点を次々にせん断しなければならず，それに必要な力が摩擦力になる。いま界面のせん断強度を単位面積当りSとすると，摩擦力FはASに等しい。摩擦係数fはF/Pであるから，上述したA＝P/pmなる関係を用いると，f＝S/pmとなる。すなわち接触する2物体の界面の強度と塑性流動を起こす圧力との比で表され，前述したクーロンの法則に一つの説明が与えられたことになる。なお，異なった物質間の摩擦においては，pmは軟らかいほうの値をとる。またSは摩擦する物質の性質のほか，表面に存在する異物質の膜，潤滑状態などによって影響をうける。
一方，ころがり摩擦の機構には，すべり摩擦と同様な固体間の凝着のほかに，表面の微小な凹凸を上下する際のポテンシャル損失，接触部の変形に伴う内部摩擦，塑性変形に要するエネルギー，接触部に生ずるわずかなすべりなどが関与している。
摩擦係数は表面状態のわずかな違いによって変化するため，同じ物質に関する測定値にもばらつきが大きい。以下には目安としての概略値を示す。
（1）清浄面の摩擦 金属は表面エネルギーの高い物質なので，空気中におかれた金属面は酸化膜や種々の汚れでおおわれているのがふつうである。高真空中などでそれらの膜を取り除いた表面では，摩擦がきわめて高くなり，銅と銅を摩擦した場合の例では，150近くまでの値が報告されている。このような値は前述した機構だけでは説明できないが，清浄面では強い凝着が起こり，真実接触点を形成する際の塑性流動に摩擦力自体も関与して，P/pmで与えられるよりも大きな接触点ができるためと説明されている。
（2）乾燥摩擦 空気中における見かけ上潤滑を行っていない場合の摩擦を便宜上乾燥摩擦と呼んでいる。もっとも摩擦係数の小さい物質として知られているのは四フッ化エチレン樹脂（PTFE）で，0.04程度の値が得られる。PTFEをはじめ，黒鉛や二硫化モリブデンなどの固体潤滑剤を配合した自己潤滑性複合材料の摩擦係数は，0.04～0.5程度である。金属の乾燥摩擦における摩擦係数の値はもう少し高く，だいたい0.4～1.2の範囲にある。
（3）境界摩擦 固体面を潤滑剤の吸着膜や潤滑剤との反応膜でおおった状態では，金属の摩擦係数としては0.1～0.3程度の値が一応の目安になるが，条件による変化が大きい。
（4）流体摩擦 軸受などで，固体面間に数μmから100μm程度の薄い流体潤滑膜を介在させた流体潤滑状態における摩擦係数は，乾燥摩擦や境界摩擦に比べてずっと小さいのが特徴である。流体として潤滑油を用いた場合には，ふつう10⁻3程度であって，気体を用いた場合には10⁻6～10⁻7の値が得られている。
（5）ころがり摩擦 金属のころがり摩擦係数の値は，10⁻3～10⁻5程度である。ころがり摩擦に対しては，潤滑はあまり効果をもたない。
→潤滑
執筆者：木村 好次
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
一つの物体が他の物体の表面に接して動きだそうとするとき、または実際に運動しているときに、その接触面に運動を妨げるような力が働く。この現象を摩擦とよび、そのときに生ずる力を摩擦力という。止まっている物体を動かそうとするときにおきる静止摩擦と、動いている物体に働く運動摩擦とがある。運動摩擦は、さらに運動の状態によって、すべり摩擦と、ころがり摩擦に分けられる。重い物体を地面の上で引きずろうとするとき、なかなか動かないのは静止摩擦のためであり、動きだしてからも大きな力を必要とするのはすべり摩擦のためである。液体や気体のいろいろな部分が異なる速度で流れている場合、隣り合った部分の間にも摩擦力が働く。このような現象を内部摩擦、または粘性とよぶ。液体や気体の中を物体が動くときに、物体の表面に平行に働く抵抗は摩擦抵抗または粘性抵抗とよばれる。空気中を進む車や航空機には空気の摩擦抵抗が働く。摩擦ということばは、通常固体表面での摩擦を意味することが多いが、このような場合は内部摩擦に対して外部摩擦とよばれることもある。一見してきれいに見える固体の表面でも、実際はいろいろな物質の薄い膜で覆われていることが多い。このような薄い吸着分子層が存在するときの摩擦を境界摩擦とよび、清浄な固体表面での摩擦を乾燥摩擦という。
［石川光男］
固体表面上で静止している物体を動かそうとしても、力が小さいうちは動きださない。これは力が小さいうちは加えた力と同じ大きさの逆向きの静止摩擦力が働くからである。力がある値以上になると動きだすのは、静止摩擦力には最大の値があり、それ以上は大きくならないからである。この限界の摩擦力を最大静止摩擦力という。その大きさは接触面の状態と、面に垂直に働く力によって決まり、接触面積の大小には無関係である。最大静止摩擦力は面に垂直に働く力に比例するが、その比例定数を静止摩擦係数という。この値が小さいほど物体を動かす力は小さくてすむ。水平板上に物体をのせ、面の傾角をしだいに増していくと、傾角がある値を超えたときに物体が滑り始める。物体が滑りだす直前の傾角を摩擦角とよぶ。のように物体の重さをW、斜面と物体との接触面に働く静止摩擦係数をμ、摩擦角をαとすると、斜面を垂直に押す力はWcosαとなるので、最大静止摩擦力はμWcosαとなる。この値は、物体が斜面に平行に滑り落ちようとする力Wsinαに等しいので、Wsinα＝μWcosαという関係がある。したがってμ＝tanαとなるので、摩擦角αを測定することによって、接触面の静止摩擦係数μが求められる。
［石川光男］
固体表面上を運動している物体に働く摩擦力は、静止摩擦の場合と同様に面に垂直に働く力に比例する。この比例定数を運動摩擦係数という。乾燥摩擦では、速度のある範囲内で、運動摩擦力は速度の大小に関係しない。また一般に運動摩擦係数は静止摩擦係数よりも小さい。この二つの実験法則は、「摩擦力は接触面に垂直に働く力に比例し、接触面積によらない」という摩擦の法則とともに、クーロンの法則またはアモントン‐クーロンの法則とよばれている。はいくつかの固体の摩擦係数を示すが、これは常識的な意味で固体表面が清浄だと思われる場合の経験的な値である。先に述べたように固体表面には種々の物質が吸着しているので、それらの吸着物質を厳密に取り除いて実験を行うと摩擦係数の値が大きく変わってくることも少なくない。このような事情から、静止摩擦力は運動摩擦力より大きいという法則をクーロンの法則から除外することもある。
物体が面を転がる場合にも静止摩擦、運動摩擦の区別があり、静止摩擦力は運動摩擦力よりも大きいが、どちらもすべり摩擦に比べるとはるかに小さい。したがって、物体を動かすときにすべり摩擦を避けてころがり摩擦を利用すると、小さな力で動かすことができる。ころや乗物の車、ボールベアリングなどは、みなころがり摩擦の小さいことを利用したものである。自転車やミシンなどで、金属が接触して滑る部分に油をさすことが多いが、これはすべり摩擦を小さくして金属が擦り減るのを防ぐためである。油の分子は金属の表面に強く結合するので、表面の油の分子どうしが接触して金属は直接に触れ合わないから、この場合は油の内部摩擦が働いている。これらは摩擦を小さくするくふうであるが、摩擦を大きくするようにくふうする場合もある。靴の底やタイヤの溝は、摩擦を大きくして滑らないようにするためである。
［石川光男］
『田中久一郎著『摩擦のおはなし』（1985・日本規格協会）』▽『岩波書店辞典編集部編、飯野徹雄他監修『科学の事典』第3版（1985・岩波書店）』▽『河野彰夫著『ポピュラー・サイエンス 摩擦の科学』（1989・裳華房）』▽『角田和雄著『摩擦の世界』（岩波新書）』
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
出典 株式会社平凡社百科事典マイペディアについて 情報
出典 平凡社「普及版 字通」普及版 字通について 情報
…機械などの摩擦面を油，グリースなどによってすべりやすくし，摩擦抵抗，摩耗，焼付きなどを減らすことを潤滑という。潤滑が不十分だと摩擦抵抗が大きく，機械の運転に大きなエネルギーを要し，設計によってはセルフロックなどのため，自動機械，ロボットなどがまったく動かなくなることすらありうる。…
※「摩擦」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
年齢を問わず、多様なキャリア形成で活躍する働き方。企業には専門人材の育成支援やリスキリング(学び直し)の機会提供、女性活躍推進や従業員と役員の接点拡大などが求められる。人材の確保につながり、従業員を...
10/29 小学館の図鑑NEO[新版]動物を追加
10/22 デジタル大辞泉を更新
10/22 デジタル大辞泉プラスを更新
10/1 共同通信ニュース用語解説を追加
9/20 日本大百科全書(ニッポニカ)を更新
