マルコフ過程（読み）マルコフカテイ（英語表記）Markov process

デジタル大辞泉

マルコフ‐かてい〔‐クワテイ〕【マルコフ過程】

次に起こる事象の確率が、現在の状態のみによって決まり、過去の振る舞いに一切依存しない確率過程。ランダムウオークなどの物理現象の時間発展に見られる。ロシアの数学者A＝マルコフが考案。

出典　小学館

改訂新版　世界大百科事典

マルコフ過程 (マルコフかてい)
Markov process

時間とともに変動する偶然量の数学的モデルとしての確率過程｛X_t，t∈T｝を考える。Tは時間の集合，X_tは時刻tごとに定まる確率変数（偶然量の値）である。X_tの値を指定すると，t以後の変量｛X_s，s≧t｝の確率法則が，t以前の変量｛X_s，s≦t｝のあり方に無関係に定まるとき，確率過程はマルコフ過程と呼ばれる。X_tの値がxであるという条件の下で，s時間後の変量X_t+sが集合Eに属する確率をマルコフ過程の推移確率という。とくにこの確率がtに依存しないとき，これをP_s（x，E）と表し，マルコフ過程を時間的に一様であるという。そのようなマルコフ過程は推移確率と初期分布，すなわちt＝0での変量X₀の分布により定まる。

　T＝｛0，1，2，……｝であり，X_tの取り得る値の集合（状態空間）が有限集合｛1，2，……，N｝の場合，マルコフ過程は有限マルコフ連鎖と呼ばれ，1906年にA.A.マルコフによって扱われた。どの成分も負でないN次正方行列Pで各行の成分の和が1に等しいものを推移行列という。時間的に一様な有限マルコフ連鎖の推移確率は推移行列Pを与えると定まり，実際行列Pのn乗Pⁿの（i，j）成分がP_n（i，j）（X_m＝iなる条件下でX_m+n＝jとなる確率）に等しい。T＝［0，∞）で，状態空間が実数の集合Rの場合，時間的に一様なマルコフ過程の推移確率P_s（x，E）を定める量として，有限マルコフ連鎖の場合のP－I（Iは単位行列）に相当する量，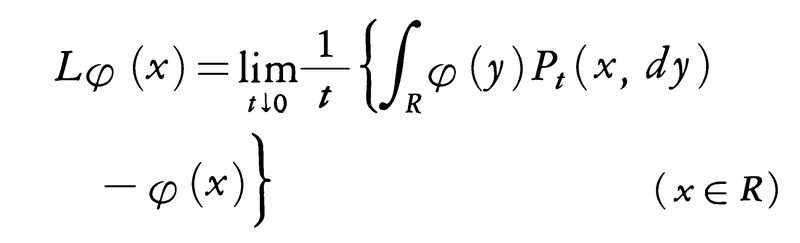

を考える。Lはマルコフ過程の生成作用素と呼ばれ，Lの型によってマルコフ過程X_tの挙動を知ることができる。多くの場合Lは次の微分作用素（1）か，積分作用素（2）か，もしくはそれらの結合となる。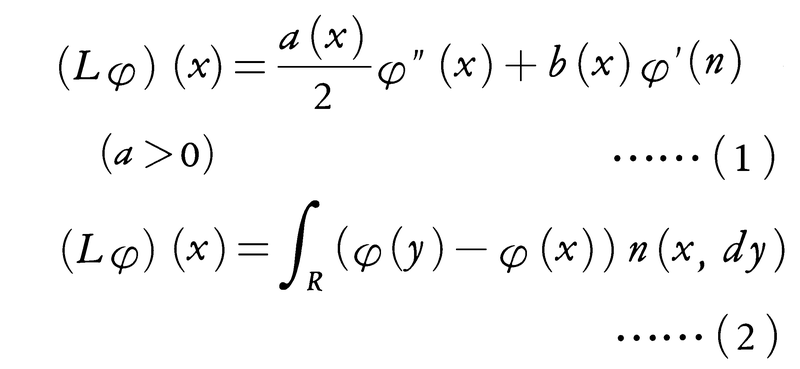

Lが表示（1）をもつとき，マルコフ過程X_tはtの関数として確率1で連続にとれ，拡散過程と呼ばれている。a（x）/2，b（x）はおのおのxから出たX_tの瞬間的変位の分散および平均を示す。（2）の場合X_tは確率1でtについて階段関数となり，n（x，dy）はxから出発したX_tが飛躍してdyに移るようすを示す。とくにa＝1，b＝0なる拡散過程はブラウン運動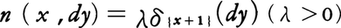，なる飛躍型マルコフ過程はポアソン過程にあたる。

　X_tの分布がxについて密度関数v_t（x）をもつとき，vは方程式∂v_t（x）/∂t＝L^＊v_t（x）の解となる。これはA.N.コルモゴロフが1931年に導いたものであり，L^＊は生成作用素Lの共役作用素である。例えばLが（1）型のとき，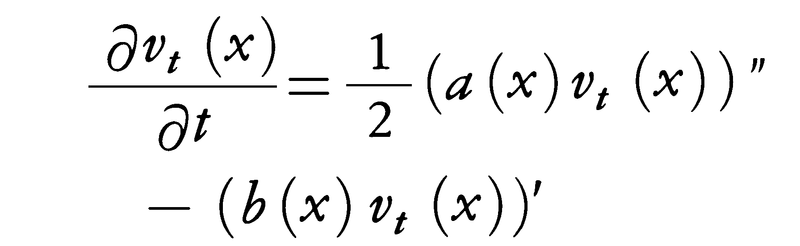

となるが，この式は拡散方程式として物理学者によってすでに研究され始めていたものである。このようにマルコフ過程は拡散現象などとのかかわり合いが深く，また以来生成作用素に関連して確率微分方程式論などの豊富な計算方法も開発されてきた確率過程である。
執筆者：福島 正俊

出典　株式会社平凡社「改訂新版　世界大百科事典」

岩石学辞典

マルコフ過程

観測が時間的順序を追って行われ，データ相互間に順序に応じた関連がある統計的な時系列データの過程の一つ．時刻tに偶然量のとる値の分布がt以前の過去の任意の一時刻t₀にとった値だけに関係し，t₀以前の履歴には影響されない確率過程．マルコフ過程のとる値が有限個または可算個のときマルコフ連鎖（Markov chain）という［長倉ほか : 1998］．堆積過程の解析などに数多く用いられている．

出典　朝倉書店

ブリタニカ国際大百科事典 小項目事典

マルコフ過程
マルコフかてい
Markov process

ロシアの数学者 A. A.マルコフが解明した理論。一連の実験があって，各実験の結果は a₁，a₂，…，a_n のいずれかで，おのおのの現れる確率がその直前の結果にだけ関係し，過去の履歴にはまったく関係しないとする。このような場合，この一連の実験をマルコフ過程またはマルコフ連鎖という。

出典　ブリタニカ国際大百科事典 小項目事典

ASCII.jpデジタル用語辞典

マルコフ過程

次に起こる事象の確率が、現在の状態に至るまでの経過とは関係なく、現在の状態によってのみ決定される確率過程のこと。たとえば、天気の移り変わりをマルコフ過程であるとし、雨の日の翌日の天気が晴れである確率が30%であるとすれば、今日の天気が雨の場合、翌日の天気が晴れになる確率は、前日までの天気の状態によらず30%となる。

出典　ASCII.jpデジタル用語辞典

法則の辞典

マルコフ過程【Markoff process】

未来が現在だけから決まり，記憶をもたない過程をいう．ある時刻にある偶然事象が起きる確率は，その一つ前の時刻にどの事象が起きたかのみに依存し，それ以前の事柄にはまったく依存しない過程である．

出典　朝倉書店

世界大百科事典（旧版）内のマルコフ過程の言及

【確率過程】より

…時刻0からtまでの間に起きるある種の交通事故の件数をX_t(ω)とするとき，｛X_t(ω)｝がポアソン過程とみなされる場合がある。　確率過程のうち，ガウス過程，定常過程，加法過程，マルコフ過程，拡散過程，マルチンゲールなどはもっともよく研究されている。
［ガウス過程］
　｛X_t(ω)｝を確率過程とする。…

※「マルコフ過程」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」